Асимптота графика функции: определение, как искать

Что такое асимптота — понятие и определение

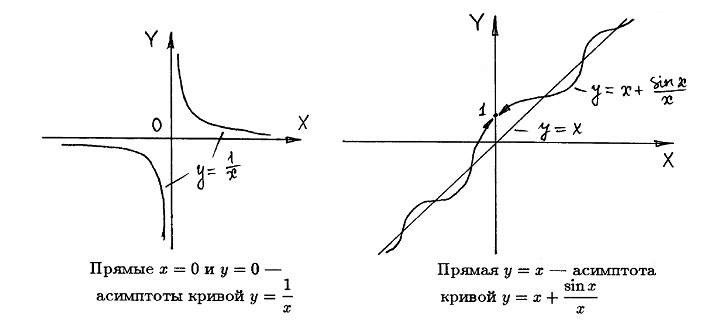
На рисунке приведены примеры асимптот графиков функций.

На рисунке слева продемонстрирована кривая, которая приближается к асимптоте и остается с одной стороны по отношению к ней.

На рисунке справа представлена кривая (график функции), которая пресекает асимптоту бесконечное множество раз с разных сторон

Асимптоты графика функции, основные виды

Асимптоты делятся на три вида: вертикальные, наклонные и горизонтальные.

У разных функции в наличии может быть различное количество асимптот:

1. Парабола и синусоида не имеют асимптот.
2. Экспоненциальная и логарифмическая функции имеют 1 асимптоту.
3. Арктангенс и арккотангенс — две.
4. Тангенс и котангенс — бесконечное количество.
5. Гипербола имеет горизонтальную и вертикальную асимптоты.

Приведем пример нахождения асимптот гиперболы.

При \(x\rightarrow+\infty\) разность ординат асимптоты и гиперболы будет \(\delta\rightarrow0\).

Это действительно, так как:

\(\delta=\frac bax-\frac ba\sqrt{x^2-a^2}=\frac ba(x-\sqrt{x^2-a^2)}=\frac ba\cdot\frac{x^2-x^2+a^2}{x+\sqrt{x^2-a^2}}=\frac ba\cdot\frac{a^2}{x+\sqrt{x^2-a^2}}\)

\(\delta\rightarrow\infty\;при\;x\rightarrow+\infty\)

Следовательно, если абсцисса х неограниченно возрастает, то график гиперболы и ее асимптота неограниченно сближаются.

Расположение асимптот гиперболы соответствует диагоналям прямоугольника, стороны которого параллельны оси Ох и оси Оу, а центром служит начало координат.

В равносторонней гиперболе, имеющей вид \(x^2-y^2=a^2\), когда \(b=a\), асимптоты будут иметь угловые коэффициенты \(k=\pm\frac ba\), равные \(\pm1\). Свойством этих асимптот является взаимная перпендикулярность. Они также делят пополам углы между осями симметрии гиперболы.

Пример

Необходимо составить уравнение гиперболы, если следующие уравнения задают ее асимптоты:

\(y=\pm\frac{\sqrt6}3x\)

Гипербола проходит через точку М(6; -4).

Решение

Применим формулу \(y=\frac bax\) и получим:

\(\frac ba=\pm\frac{\sqrt6}3\)

Подставим координаты точки М в общую формулу уравнения гиперболы:

\(\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\)

Получим систему уравнений. Чтобы получить уравнение данной гиперболы, необходимо вычислить полученную систему уравнений.

\(\left\{\begin{array}{l}\frac{6^2}{a^2}-\frac{{(-4)}^2}{b^2}=1,\\\frac ba=\pm\frac{\sqrt6}3\end{array}\right.\Rightarrow a=\pm\sqrt{12},\;b=\sqrt8\)

В итоге получим:

\(\frac{x^2}{12}-\frac{y^2}8=1\)

Вертикальные асимптоты

Если хотя бы один из пределов \(\lim_{x\rightarrow c-0}f(x)\) или \(\lim_{x\rightarrow c+0}f(x)\) является равным +∞ или —∞, то вертикальной асимптотой графика функции у=f(x) будет являться прямая х=с.

Другое определение подразумевает, что если в определении асимптоты х0 является конечным числом, то такая асимптота является вертикальной. При этом в точке левый или правый предел (или оба) равны +∞ или -∞.

Примеры вертикальных асимптот:

Пример 1

Необходимо определить вертикальную асимптоту функции \(\lim_{x\rightarrow+\infty}a(x)=0.\)

Решение

Так как

\(\lim_{x\rightarrow0+0}(4+\frac1x)=+\infty\)

\(\lim_{x\rightarrow0-0}(4+\frac1x)=-\infty\)

то x=0 — вертикальная асимптота.

Пример 2

Имеем \(y=2^{1/x}\).

Ось ординат является вертикальной асимптотой, так как

\(\lim_{x\rightarrow0-0}2^{1/x}=0\)

\(\lim_{x\rightarrow0+0}2^{1/x}=\infty\)

Наклонные асимптоты

Если в определении асимптоты присутствует +∞ или —∞, то она относится либо к горизонтальной, либо к наклонной.

Асимптота графика функции у=f(x) является наклонной, если эту функцию можно представить в виде f(x)=kx+b+а(х). При этом должно выполняться условие: \(a(x)\rightarrow0\) при \\(x\rightarrow+\infty\). Прямая будет иметь вид y=kx+b.

Прямая у=kx+b будет наклонной асимптотой при \(x\rightarrow+\infty\) и \(x\rightarrow-\infty\), если существуют пределы:

\(\lim_{x\rightarrow+\infty}\frac{f(x)}x=k\)

\(\lim_{x\rightarrow+\infty}\left[f(x)-kx\right]=b\)

Если k=0, то наклонная асимптота превращается в горизонтальную.

Применение правила Лопиталя

Правило Лопиталя применяется, когда границы не определены, например, 0/0 или ∞/∞:

\(\lim_{x\rightarrow a}\frac{f(x)}{g(x)}=\left\{\frac00\right\}\) или \(\lim_{x\rightarrow a}\frac{f(x)}{g(x)}=\left\{\frac\infty\infty\right\}\)

Если функции можно дифференцировать, и они относятся к окрестностям точки x=a, тогда наклонную асимптоту необходимо искать по формуле:

\(\lim_{x\rightarrow a}\frac{f(x)}{g(x)}=\lim_{x\rightarrow a}\frac{f'(x)}{g'(x)}\)

Производная может применяться многократно для получения константы в числителе или знаменателе.

Пример 1

Имеется функция:

\(y=x+\frac1x\)

\(k=\lim_{x\rightarrow\infty}\frac yx=\lim_{x\rightarrow\infty}\frac{x+{\displaystyle\frac1x}}x=\lim_{x\rightarrow\infty}(1+\frac1{x^2})=1\)

\(b=\lim_{x\rightarrow\infty}(y-kx)=\lim_{x\rightarrow\infty}(x+\frac1x-x)=\lim_{x\rightarrow\infty}\frac1x=0\)

Прямая у=х — наклонная асимптота графика данной функции.

Пример 2

Имеется функция \(y=\frac{\left|x\right|(x-1)}{x+1}.\)

Рассмотрим два варианта:

x>0 и x<0.

Если x>0, то

\(k_1=\lim_{x\rightarrow+\infty}\frac yx=\lim_{x\rightarrow+\infty}\frac{\left|x\right|(x-1)}{x(x+1)}=\lim_{x\rightarrow+\infty}\frac{x(x-1)}{x(x+1)}=1\)

\(b_1=\lim_{x\rightarrow+\infty}(y-k_1x)=\lim_{x\rightarrow+\infty}\left(\frac{\left|x\right|(x-1)}{x(x+1)}-x\right)=\lim_{x\rightarrow+\infty}\frac{x(x-1)-x(x+1)}{x+1}=-2\)

То есть правая ветвь кривой имеет наклонную асимптоту в виде прямой у=х-2.

Если x<0, то

\(k_2=\lim_{x\rightarrow-\infty}\frac yx=\lim_{x\rightarrow-\infty}\frac{\left|x\right|(x-1)}{x(x+1)}=\lim_{x\rightarrow-\infty}\frac{(-x)(x-1)}{x(x+1)}=-1\)

\(b_2=\lim_{x\rightarrow-\infty}(y-k_2x)=\lim_{x\rightarrow-\infty}\left(\frac{\left|x\right|(x-1)}{x+1}+x\right)=\lim_{x\rightarrow-\infty}\frac{(-x)(x-1)+x(x+1)}{x+1}=2\)

То есть левая ветвь кривой имеет наклонную асимптоту в виде прямой у=-х+2.

Горизонтальные асимптоты

Прямая y=b является горизонтальной асимптотой для графика функции y=f(x), если

\(\lim_{x\rightarrow+\infty}f(x)=\lim_{x\rightarrow-\infty}f(x)=b\)

При \(x\rightarrow+\infty\) или при \(x\rightarrow-\infty\), когда только один из представленных пределов равен числу b, прямая y=b становится горизонтальной асимптотой не всей кривой, а соответствующей ее части.

Пример 1

Имеется функция: \(y=4+\frac1x.\)

\(\lim_{x\rightarrow+\infty}\left(4+\frac1x\right)=\lim_{x\rightarrow-\infty}\left(4+\frac1x\right)=4\)

поэтому y=4 — горизонтальная асимптота данной функции.

Пример 2

Имеется \(y=2^{1/x}\).

Здесь \(\lim_{x\rightarrow+\infty}2^{1/x}=\lim_{x\rightarrow-\infty}2^{1/x}=1\).

Значит, у=1 — горизонтальная асимптота графика функции.

Пример 3

Имеется \(y=2^{-x}.\)

Так как 

\(\lim_{x\rightarrow+\infty}=2^{-x}=0\)

\(\lim_{x\rightarrow-\infty}=2^{-x}=+\infty\)

то y=0 — горизонтальная асимптота графика функции при \(x\rightarrow+\infty\).