Способы расчета периметра круга и длины окружности
Периметр круга — что это, определение
Круг — это геометрическое множество точек на плоскости, расстояние от которых до данной точки, называемой центром круга, не превосходит заданного неотрицательного числа.
Окружность — замкнутая кривая на плоскости, все точки которой равноудалены от центра окружности.
Эти определения плотно связаны друг с другом. Круг — это часть плоскости, ограниченная окружностью. Окружность — это граница круга.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
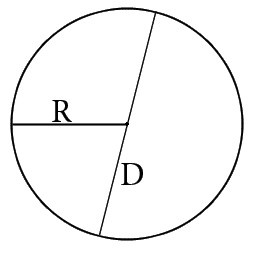
Радиус — расстояние от центра окружности до любой ее точки. Это отрезок, который соединяет центр круга с его границей.
Диаметр — это отрезок, соединяющий две точки окружности и проходящий через ее центр. Он равен двум радиусам.
Периметр — это длина окружности, ограничивающей круг.
Понятия «периметр круга» и «длина окружности» считаются синонимичными.
Как рассчитать периметр круга или длину окружности
Чтобы вычислить периметр круга, необходимо ввести постоянную величину — число Пи. Оно равно отношению длины окружности к ее диаметру. Это отношение идентично для всех окружностей и равно \(\pi=3,14159...\)
Чтобы произвести расчет периметра круга, достаточно помнить это число до двух знаков после запятой:
\(\pi=3,14\)
Помимо этого, для вычисления необходимо знать длину радиуса или диаметра.
Через радиус
Длину окружности L можно найти по формуле через радиус:
\(L=2\pi R\)
где \(\pi \) — число Пи, R — радиус.
Через диаметр
Длину окружности L можно найти по формуле через диаметр. Поскольку диаметр D равен двум радиусам:
\(L=\pi D\)
Примеры решения задач
Задача
Каков периметр круга, если его радиус равен 0,5 см?
Решение
По формуле, \(L= 2\pi R\). Отсюда:
\(L=2\pi R=2\cdot0,5\pi=\pi\approx3,14\)
Ответ: 3,14 см.
Задача
Какова длина окружности, если ее диаметр равен 2 см?
Решение
По формуле, \(L=\pi D\). Отсюда:
\(L=\pi D=\pi\cdot2\approx3,14\cdot2=6,28\)
Ответ: 6,28 см.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так