Площадь поверхности параллелепипеда

Что такое площадь поверхности параллелепипеда

В общем случае площадь — это численное значение, характеризующее размер двумерной геометрической фигуры.

Параллелепипед может существовать только в трех измерениях, поэтому для него вводится понятие площади поверхности. В геометрическом смысле площадь поверхности объемной фигуры является совокупностью площадей ее граней.

Формула нахождения полной площади

В задачах чаще всего имеется дело с прямоугольным параллелепипедом. Для него полная площадь поверхности вычисляется следующим образом:

\(S=2\cdot(a\cdot b+a\cdot c+b\cdot c)\)

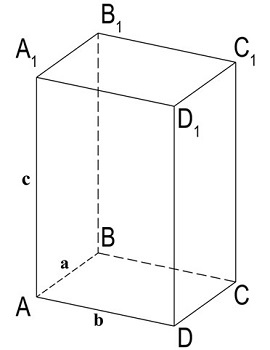
где a, b и c — длины ребер, исходящих из любой вершины параллелепипеда.

Рассмотрим то, как данная формула выводится. Как уже упоминалось выше, площадь поверхности объемной фигуры является совокупностью площадей ее граней. Для наглядности возьмем параллелепипед ABCDA₁B₁C₁D₁.

Полная площадь его поверхности равняется сумме площадей всех граней: \(S_{пар}=S_{AA_1D_1D}+S_{DD_1C_1C}+S_{CC_1B_1B}+S_{BB_1A_1A}+S_{ABCD}+S_{A_1B_1C_1D_1}\)

Согласно свойствам параллелепипеда, его противоположные грани равны между собой. Следовательно, нет необходимости вычислять площадь всех шести граней, можно ограничиться тремя, а затем их сумму умножить на 2:

\(S_{пар}=2\cdot\left(S_{AA_1D_1D}+S_{BB_1A_1A}+S_{ABCD}\right)\)

Грани прямого параллелепипеда являются прямоугольниками. Площадь данной фигуры равняется произведению ее сторон:

\(S_▭=a\cdot b\)

У выбранных нами для расчета площади граней есть три общие стороны: AB, AD и AA₁. Для удобства обозначим их как a, b и c соответственно.

Таким образом:

 \(S_{ABCD}=a\cdot b\)

\(S_{AA_1D_1D}=a\cdot c\)

\(S_{BB_1A_1A}=b\cdot c\)

Подставим данные значения в обозначенную выше формулу площади параллелепипеда:

\(S_{пар}=2\cdot\left(a\cdot b+a\cdot c+b\cdot c\right)\)

Вычисление площади боковой поверхности прямоугольного параллелепипеда

Кроме полной площади поверхности, в расчетах иногда необходимо вычислить площадь боковой поверхности, то есть совокупность площадей боковых граней, без учета оснований.

Для этого есть три взаимосвязанные формулы:

1. \(S_{бок}=P_{осн}\cdot h,\) где \(P_{осн}\) — периметр основания параллелепипеда; h — высота. На рисунке выше она равняется стороне, обозначенной как c.
2. \(S_{бок}=2\cdot a\cdot c+2\cdot b\cdot c\), где a, b и c — длины ребер, исходящих из любой вершины параллелепипеда.
3. \(S_{бок}=2\cdot c\cdot(a+b).\)

Примеры решения задач

Задача

Вычислить полную площадь поверхности прямоугольного параллелепипеда ABCDA₁B₁C₁D₁.

Дано: AB = 3, A₁B = 6, AD = 5.

Решение

Для расчета полной площади необходимо знать длины трех сторон. В данном случае нам понадобится вычислить длину стороны AA₁. Так как длина диагонали A₁B известна, сделать это нетрудно.

Воспользуемся теоремой Пифагора:

\(A_1B=\sqrt{{AA_1}^2+{AB}^2}\)

Соответственно, \({AA_1}=\sqrt{{A_1B}^2-{AB}^2}=\sqrt{6^2-3^2}=\sqrt{36-9}=\sqrt{25}=5\)

Подставим известные значения в формулу расчета площади поверхности:

\(S=2\cdot(a\cdot b+a\cdot c+b\cdot c)\)

\(S=2\cdot(AB\cdot AD+AB\cdot AA_1+AD\cdot AA_1)=2\cdot(3\cdot5+3\cdot5+5\cdot5)=2\cdot(15+15+25)=2\cdot55=110\)

Ответ: S=110.

Задача 2

Вычислить длину стороны прямого параллелепипеда ABCDA₁B₁C₁D₁.

Дано: S_пов=96, S_бок=60, b=6.

Решение

Так как нам известна одна из сторон основания — b а в основании параллелепипеда лежит прямоугольник, найти вторую сторону проще всего будет через площадь этого основания:

\(S=a\cdot b\)

Отличие площади боковой поверхности от полной в том, что в ней не учитываются нижняя и верхняя грани фигуры. Следовательно, их разность будет равняться двум площадям основания. Вычислим это значение:

\(S_{пов}-S_{бок}=2\cdot a\cdot b+2\cdot a\cdot c+2\cdot b\cdot c-2\cdot a\cdot c-2\cdot b\cdot c=2\cdot a\cdot b\)

Преобразуем выражение так, чтобы вычислить длину неизвестной стороны:

\(2\cdot a\cdot b=S_{пов}-S_{бок}\)

\(a=\frac{S_{пов}-S_{бок}}{2\cdot b}=\frac{96-60}{2\cdot6}=\frac{36}{12}=3\)

Ответ: a=3.