Как посчитать площадь треугольника
Что такое площадь треугольника
Треугольник — это многоугольник с тремя сторонами и тремя вершинами.
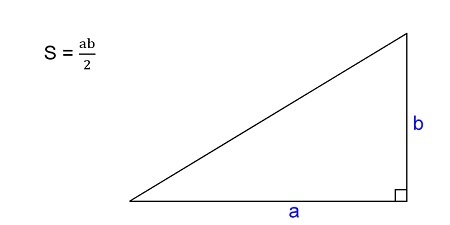
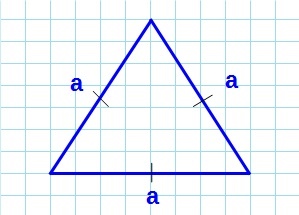
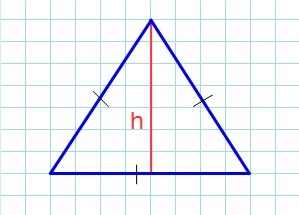
Площадь треугольника — это величина плоскости, заключенной между сторонами этой геометрической фигуры.У треугольника она равна произведению половины основания на высоту.
Математически это выглядит так:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
\(S=\frac12a\times h\)
где a — основание треугольника, а h — его высота.
Способы нахождения площади
Но существуют также и другие способы, по которым можно найти S этого многоугольника. Рассмотрим основные из них.
Через две стороны и угол
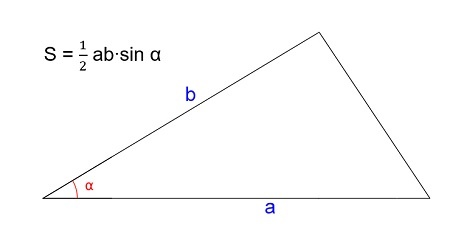
Если вам известны две стороны любого треугольника и угол между ними, найти площадь можно по формуле:
\(S=\frac12a\times b\times\sin\alpha\)
где a и b — стороны фигуры, а α — угол между ними.
Через радиус описанной окружности и три стороны
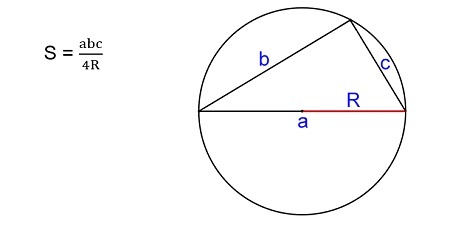
Если вам известен радиус окружности, которая описана вокруг вашего треугольника, а также все его стороны, можно вычислить S следующим образом:
\(S=\frac{a\times b\times c}{4\times R}\)
где a, b и c — стороны фигуры, а R — радиус описанной окружности.
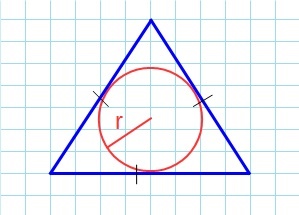
Через радиус вписанной окружности и три стороны
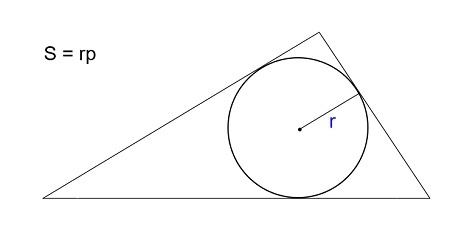
В случае, если вам известны все три стороны и радиус вписанной в треугольник окружности, можно найти его площадь по формуле:
\(S=r\times\frac{a+b+c}2\)
где r — радиус вписанной окружности, \(\frac{a+b+c}2\) — полупериметр фигуры.
Таким образом, формулу можно выразить всего двумя множителями:
\(S=r\times p\)
где p — полупериметр треугольника.
Через сторону и два угла
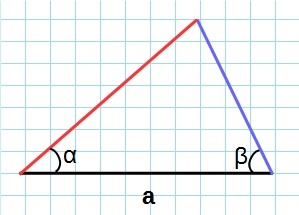
Если в данной фигуры вам известна лишь одна сторона и две прилегающих к ней угла, ее S можно найти следующим образом:
\(S=\frac12\times a^2\times\frac{\sin\alpha\times\sin\beta}{\sin\gamma}\)
причем \(\gamma=180^\circ-(\alpha+\beta)\)
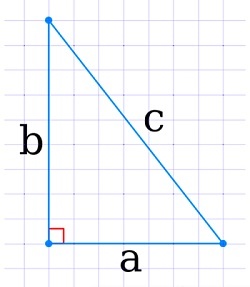
Для прямоугольного треугольника
В случае треугольника с прямым углом формулы для нахождения площади будут немного отличаться. Найти S можно будет несколькими способами.
По двум сторонам
Если вам известны оба катета данной фигуры, рассчитать S можно умножив их друг на друга, а потом разделив на пополам:
\(S=\frac{a\times b}2\)
где a и b — катеты прямоугольного треугольника.
Через гипотенузу и острый угол
Зная длину гипотенузы и величину одного из острых углов, мы можем найти один из его катетов по определению косинуса. И уже потом можем использовать формулу для нахождения площади треугольника через две стороны и синус угла между ними.
Начнем с поиска катета:
\(\cos\left(\alpha\right)=\frac ac\)
\(a=c\times\cos\left(\alpha\right)\)
где c — гипотенуза треугольника, a — его катет, а α — угол между ними.
Подставляем получившееся значение в формулу \(S=\frac12a\times c\times\sin\alpha\), получается:
\(S=c^2\times\cos\left(\alpha\right)\times\sin\left(\alpha\right)\)
Через катет и прилежащий угол
В этом случае нужно будет использовать следующую формулу:
\(S=\frac12\times a^2\times\tan\left(\alpha\right)\)
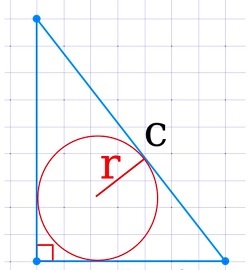
Через радиус вписанной окружности и гипотенузу
Зная радиус вписанной в данную фигуру окружности и гипотенузу, мы можем использовать следующее уравнение для расчета:
\(S=r\times(r+c)\)
где r — радиус вписанной окружности, c — гипотенуза.
Через вписанную окружность
Радиус, опущенный в точку касания окружности и гипотенузы прямоугольного треугольника, делит эту гипотенузу на неравные отрезки. Если нам известны величины этих отрезков, мы можем найти площадь фигуры по формуле:
\(S=с_1\times с_2\)
где \(с_1\) и \(с_2\) — неравные отрезки гипотенузы.
По формуле Герона
Если мы знаем длины всех сторон данного многоугольника, мы можем рассчитать S по формуле Герона:
\(S=(p-a)\times(p-b)\)
где \(p=\frac{a+b+c}2\) — полупериметр фигуры.
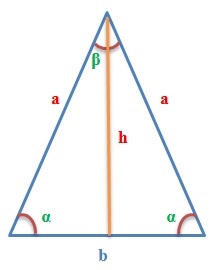
Для равнобедренного треугольника
Рассмотрим случаи нахождения площади, если у треугольника равные боковые стороны.
Через основание и сторону
В этом случае формула будет выглядеть следующим образом:
\(S=\frac b4\sqrt{4a^2-b^2}\)
где a — одно из боковых ребер фигуры, а b — ее основание.
Через основание и противолежащий угол
Зная длину основания и противолежащий ему угол, мы можем использовать следующую формулу:
\(S=\frac{b^2}{4\tan\left({\displaystyle\frac\beta2}\right)}\)
где b — основание многоугольника, β — противолежащий ему угол.
Через основание и высоту
Если нам известна величина основания равнобедренного треугольника, а также его высота, найдем S по приведенной ниже по элементарной формуле:
\(S=\frac{b\times h}2\)
где b — основание фигуры, а h — высота, проведенная к этому основанию.
Через боковые стороны и угол между ними
Если мы знаем длину боковых сторон и угол между ними, найдем площадь, опираясь на расчеты:
\(S=\frac12a^2\times\sin\left(\beta\right)\)
где a — это боковое ребро, β — угол между равными ребрами.
Через основание и угол между боковыми сторонами
В этом случае нам сначала придется найти высоту по формуле:
\(h=\frac b2\tan\left(\beta\right)\)
где β — угол при вершине, а b — основание.
Далее подставляем значение в формулу
\(S=\frac{b\times h}2 = \frac{b\times{\displaystyle\frac b2}\tan\left(\beta\right)}2=\frac{b^2\tan\left(\beta\right)}4\)
Итоговая формула:
\(S=frac{b^2\tan\left(\beta\right)}4\)
Для равностороннего треугольника
В треугольнике, у которого все стороны равны, способы нахождения S также имеют свою специфику.
Через радиус описанной окружности
Если вокруг данного многоугольника описали окружность и нам известен ее радиус, расчеты будут такими:
\(S=\frac{3\sqrt3R^2}4\)
где R — радиус описанной окружности.
Через радиус вписанной окружности
В этом случае воспользуемся таким уравнением:
\(S=3\sqrt3r^2\)
где r — радиус вписанной в многоугольник окружности.
Через сторону
Зная лишь одно ребро у равностороннего треугольника, мы можем найти S:
\(S=\frac{\sqrt3a^2}4\)
где a — сторона фигуры.
Через высоту
Если нам известна только высота, можем вычислить S таким образом:
\(S=\frac{h^2}{\sqrt3}\)
Примеры решения задач
Разберемся с нахождением площади треугольника наглядно на примере некоторых случаев.
Задача 1
В треугольник вписана окружность с радиусом 6 см. Известно, что его стороны равны 10 см, 12 см и 14 см. Определить площадь фигуры.
Решение
Для расчета будем использовать формулу \(S=r\times\frac{a+b+c}2\) или \(S=r\times p\). Подставляем имеющиеся значения и получается:
\(S=6\times\frac{10+12+14}2=6\times18=108\) \(см^2\)
Ответ: \(108\) \(см^2\).
Задача 2
Дан равносторонний треугольник, вокруг которого описали окружность с радиусом 3 см. Посчитать S данной фигуры.
Решение
Считать будем, опираясь на следующее уравнение \(S=\frac{3\sqrt3R^2}4\). Подставляем данные величины и получаем:
\(S=\frac{3\sqrt33^2}4=\frac{27\sqrt3}4 см^2\)
Ответ: \(\frac{27\sqrt3}4 см^2.\)
Задача 3
Известно, что у равнобедренного треугольника основание равно 4 см, а стороны по 3 см. Нужно вычислить площадь фигуры.
Решение
Для расчета S используем формулу \(S=\frac b4\sqrt{4a^2-b^2}\). Получается:
\(\frac44\sqrt{4\times3^2-4^2}=\sqrt{36-16}=\sqrt{20}=2\sqrt5 см^2\)
Ответ: \(2\sqrt5 см^2.\)
Задача 4
Дан треугольник с прямым углом, у которого гипотенузы равна 2 см, а один из острых углов равен \(30^\circ\). Узнать S данной фигуры.
Решение
Для расчетов будем ориентировать на следующее уравнение: \(S=c^2\times\cos\left(\alpha\right)\times\sin\left(\alpha\right)\). Подставляем известные значения:
\(S=2^2\times\frac{\sqrt3}2\times\frac12=\sqrt3 см^2\)
Ответ: \(S=2^2\times\frac{\sqrt3}2\times\frac12=\sqrt3 см^2\).
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так