Как найти среднюю линию треугольника

Свойства и признаки

Признак средней линии: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок называется средней линией данного треугольника.

Свойства:

1. Равна половине длины основания и параллельна ему.
2. Отсекает треугольник, подобный данному с коэффициентом 1/2; его площадь равна четверти площади данного.
3. Три средние линии разделяют исходную фигуру на четыре равных треугольника. Центральный из них называют дополнительным треугольником.
4. Три средние линии разделяют исходный прямоугольный треугольник на четыре равных прямоугольных треугольника.

Формула для расчета

Теорема

Средняя линия треугольника параллельна основанию и равна её половине.

\(A_1C_1=\frac12AC\)

Доказательство

Дано: 

\(\triangle ABC\)

\(A_1C_1\)- средняя линия

Доказать:

\(A_1C_1\parallel AC\)

\(A_1C_1=\frac12AC\)

Рассмотрим \(\triangle BA_1C_1\) и \(\triangle BAC\):

\(\left\{\begin{array}{l}\angle B\;-\;общий\\\frac{BA_1}{BA}=\frac{BC_1}{BC}=\frac12\end{array}\right.\)

Из этого следует, что треугольники подобны по двум пропорциональным сторонам и углу между ними.

Следовательно, \(\angle BA_1C_1=\angle BAC\) , как соответственные элементы подобных треугольников. Следовательно \(A_1C_1\parallel AC\) по признаку параллельности.

Кроме того, из подобия следует, что \(\frac{A_1C_1}{AC}=\frac12\)

Следовательно, \(A_1C_1=\frac12AC\)

Утверждение доказано.

Примечание

Данная формула одинаково работает для любого треугольника: равнобедренного, равностороннего (правильного).

Задачи на использование теоремы

Задача 1

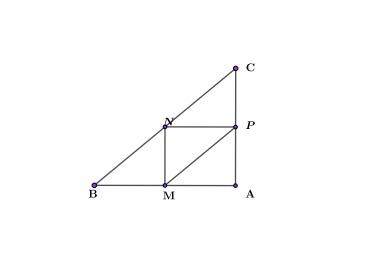
В прямоугольном треугольнике ABC проведены средние линии: MN; NP; MP. При этом MN=NP=2. Найти площадь треугольника ABC.

Рассмотрим прямоугольный треугольник NMP: 

\(S_{\triangle NMP}=\frac12\times MN\times NP=\frac12\times2\times2=2\)

Все маленькие треугольники равны, следовательно \(S_{\triangle ABC}=2\times4=8\)

Ответ: 8

Задача 2

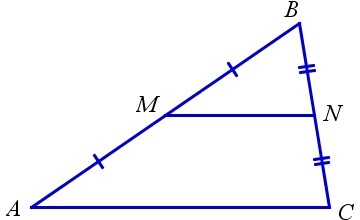
Площадь треугольника ABC равна 8. MN — средняя линия. Необходимо вычислить площадь треугольника BMN.

\(S_{\triangle BMN}=\frac14S_{\triangle ABC}=\frac14\times8=2\)

Ответ: 2

Задача 3

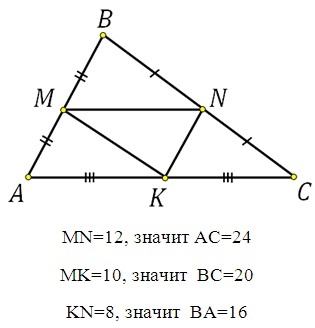
В треугольнике ABC точки M, N, K – середины сторон AB, BC, AC соответственно, MN=12, MK=10, KN=8. Необходимо узнать периметр треугольника ABC.

Средняя линия равна половине основания, следовательно находим:

MN = 12 ⇒ AC = 24

MK = 10 ⇒ BC = 20

KN = 8 ⇒ BA = 16

Значит, \(P_{\triangle ABC}=24+20+16=60\)

Ответ: 60