Доказательства теоремы Пифагора

Этот одна из базовых теорем евклидовой геометрии, определяющая соотношение между сторонами в прямоугольном треугольнике. Несложность доказательства и широкое применение обеспечили ей массовую известность.

Теорема Пифагора — краткая история

Соотношение между сторонами прямоугольного треугольника в том или ином виде было известно многим древним цивилизациям (египетской, шумерской и др.), но первая известная формулировка принадлежит греческому философу и математику Пифагору в V в. до н.э. Об этом известно из труда «Начала», который написал Евклид приблизительно в 300 г. до н. э.

Теорема Пифагора используется для доказательства многих других теорем геометрии. Математиками разработано несколько обобщений, например, для произвольных треугольников, для многомерных пространств. При этом, теорема Пифагора выполняется только в евклидовых геометриях, в иных случаях она не действует.

Формулировка теоремы

Изначальная (геометрическая) формулировка Пифагора гласила:

Позднее появился алгебраический вариант:

Оба этих определения эквивалентны. Алгебраическое более элементарно, так как оно не оперирует понятием площади, поэтому теорему в этом виде можно проверить просто – измерив длину гипотенузы и катетов, сделав затем необходимое вычисление.

Уравнение

В виде формулы теорема Пифагора записывается следующим образом:

a²+b²=c², где:

• а и b – длины двух катетов,
• с – длина гипотенузы.

Доказательство через подобные треугольники

Это доказательство – одно из наиболее простых, так как является прямым следствием аксиом и не оперирует понятием площади.

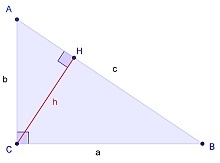
Имеется прямоугольный треугольник ABC, где C = 90º. Высота, проведенная из прямого угла пересечет гипотенузу в точке H.

Полученные треугольники ACH и CHB подобны треугольнику АВС по двум углам. Отсюда получаем:

CB/AB=HB/CB, AC/AB=AH/AC

Это соответствует:

CB²=ABxHB, AC²=ABxAH

Сложив между собой квадраты катетов, получаем:

AC²+CB²=ABx(HB+AH)=AB²

Это и требовалось доказать.

Другие способы доказательства теоремы

Зафиксировано более 400 доказательств теоремы Пифагора. Это связано с простотой ее формулировки, популярностью и широким применением в геометрии. К числу распространенных доказательств относятся методы площадей и бесконечно малых.

Методом площадей

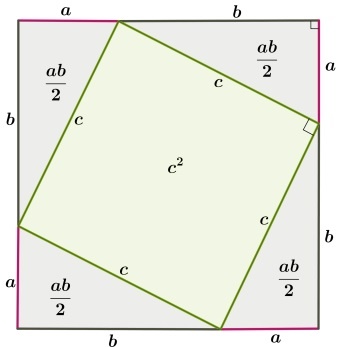
Первоначально требуется дополнительное построение – рисуется квадрат, каждая из сторон которого равна сумме длин катетов a и b. Отложив эти длины, проведем гипотенузы у прямоугольных треугольников:

Очевидно, что внутренний четырехугольник, образованный четырьмя гипотенузами, будет квадратом, так как все его стороны равны, а углы прямые. Последнее следует из того, что сумма двух углов треугольника, построенных на гипотенузе равна 90º. Вычитая это значение из развернутого угла в 180º получаем как раз прямой угол.

Площадь внешнего квадрата включает в себя:

• сумму площадей четырех прямоугольных треугольников;
• площадь внутреннего квадрата.

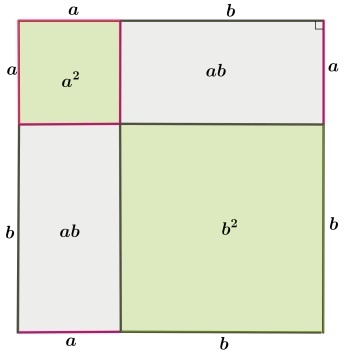
Изменив расположение отрезков на сторонах квадрата и проведя новое построение, можно получить два внутренних квадрата и два прямоугольника. При этом, прямоугольники всегда будут равны, а квадраты будут равными только в частном случае – при равенстве сторон a и b.

Значит:

4ab²=2ab ⇒ c²=a²+b², что и нужно было доказать.

Методом бесконечных малых

Данное доказательство делается с помощью интегрального исчисления. Рассматривается ситуация для бесконечно малых приращений сторон треугольника, составляется дифференциальное уравнение и находится его производная.

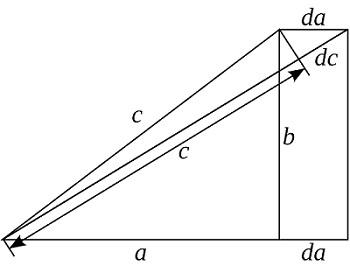
В начале вводится величина d. На это значение увеличивается катет а и гипотенуза с, а катет b остается неизменным. Отсюда имеем

da/ca = c/a, b = const

Разделяя переменные составляется дифференциальное уравнение:

c x dc = a x da

Для его решения необходимо проинтегрировать обе части, при этом получается соотношение:

c² = a² + const

определяя из начальных условий константу интегрирования, получим:

a = 0 ⇒ c² = b² = const

Таким образом мы определяем, что

c² = a² + b²

Теорема доказана!

Следствие из теоремы Пифагора

Его так же называют обратной теоремой Пифагора:

В алгебраическом виде это можно представить так:

c2=a2+b2, где:

• c – гипотенуза треугольника;
• a и b – его катеты.

Применение теоремы

Благодаря своей универсальности, теорема Пифагора находит себе применение в разных областях математики и других наук. К числу преимуществ ее применения относится прозрачность производимых вычислений.

Расстояние между точками

Одно из главных применений – это определение расстояния между двумя точками в прямоугольной системе координат:

\(\ s=\sqrt{(a-с)^{2} + (b-d)^{2}}\), где:

• s – необходимое расстояние;
• (a; b) и (с; d) – координаты двух точек.

Евклидова метрика

В этом случае с помощью теоремы Пифагора находится расстояние в многомерном пространстве:

\(d(p,\;q)=\sqrt{\sum_{i=1}^n{(p_i-q_i)}^2}\), где:

• n – число измерений данного пространства;
• d (p, q) – необходимое расстояние;
• p(p₁,….,pn) и q(q₁,….,q_n) – две точки, расстояние между которыми нужно найти.

Теория чисел

Арифметическим аналогом теоремы Пифагора стали пифагоровы тройки чисел.

Например, к таким числам можно отнести группы (3, 4, 5), (6, 8, 10), (5, 12, 13) и другие. Пифагоровы тройки широко применяются в разных областях деятельности, например, в программировании и криптографии.

Примеры решения задач

Задача 1

В прямоугольном треугольнике АВС, катет ВС = 36 см, гипотенуза АВ = 85 см. Необходимо найти катет АС.

Решение

По теореме Пифагора ВС²+АС²=АВ², значит

\(АС\;=\;\sqrt{АВ^2\;-\;АС^2}\)

Для нахождения ответа подставим в формулу исходные значения:

\(АС\;=\;\sqrt{85^2\;-\;36^2}\;=\;\sqrt{7225\;-\;1296\;}={\;\sqrt{5929}\;=\;77\;}\)

Задача 2

Является ли прямоугольным треугольник со сторонами 46, 56 и 76 см.

Решение. Если указанный треугольник прямоугольный, то две меньшие стороны в 46 и 56 см – это катеты, а большая, в 76 см – гипотенуза. По теореме Пифагора сумма квадратов катетов должна быть равна квадрату гипотенузы. Проверим это:

• 46²+56²= 5252;
• 76²= 5776;
• 5252 ≠ 5776, значит, указанный треугольник не является прямоугольным.

Задача 3.

Диагонали ромба ABCD равны 24 и 18 см. Чему равна сторона ромба.

Решение

Диагонали ромба AC и BD пересекаются под прямым углом и точкой пересечения O делятся пополам. В этом виде задача сводится к поиску гипотенузы АВ в прямоугольном треугольнике ABO с катетами АО=24/2=12 см и ВО=18/2=9 см.

По теореме Пифагора:

АО²+BO²=AB², значит

\(АС\;=\;\sqrt{85^2\;-\;36^2}\;=\;\sqrt{7225\;-\;1296\;}={\;\sqrt{5929}\;=\;77\;}\)