Термодинамика

Что такое термодинамика

В задачи термодинамики не входит изучение микроскопических величин, то есть размеров атомов и молекул, их массы и количества. С помощью термодинамических законов установлены закономерности, которым подчиняются непосредственно наблюдаемые физические величины, в том числе давление р, объем V, температура Т.

Задача термодинамики — феноменологическое рассмотрение свойств вещества. В процессе исследований состояния данных веществ характеризуют с помощью макроскопических параметров. В основе термодинамики лежат три начала, которые содержат пояснения к термодинамическим процессам.

Ключевые законы термодинамики отражают поведение энергии. Термодинамические процессы, как правило, изучают с помощью модели под названием идеальный газ.

Основные понятия термодинамики

Термодинамика является разделом молекулярной физики. В рамках предметной области изучают разнообразные свойства тел и изменения состояния вещества. По сравнению с молекулярно-кинетической теорией, представляющей собой вторую составную часть молекулярной физики, и электродинамикой термодинамика отличается тем, что исследует макроскопические свойства тел и явлений без учета их молекулярного строения. Однако, не рассматривая поведение атомов и молекул, наука термодинамика помогает определить характеристики течения микропроцессов.

Термодинамику считают количественной теорией тепловых процессов. В XIX веке бал открыт закон сохранения энергии, что послужило триггером для дальнейших термодинамических исследований. Появление термодинамики связывают с необходимостью в получении оптимальных условий использования теплоты во время совершения работы. Данный раздел молекулярной физики стал отправной точкой активного развития науки задолго до признания молекулярно-кинетической теории. Ученые пришли к выводу, что для изучения многих свойств веществ не обязательно рассматривать их строение.

Термодинамика представляет собой теорию тепловых явлений. Данный раздел не предполагает изучение молекулярного строения вещества и называется описательной или феноменологической теорией.

В основе термодинамики три фундаментальных закона, называемых началами термодинамики. Данные закономерности были установлены в качестве обобщения большого массива эмпирических фактов. Выводы термодинамики обладают общим характером.

Количество теплоты

Количество теплоты обозначают, как Q. В СИ единицами измерения данного параметра являются Дж.

Удельную теплоемкость обозначают буквой «с». В СИ единицами измерения данной характеристики являются Дж/(кг*К).

Удельная теплоемкость характеризуется не только с помощью свойств вещества, но и определяется типом процесса осуществления теплопередачи. В связи с этим, рассматривают:

• удельную теплоемкость газа в условиях постоянного давления, то есть \(c_{P}\);
• удельную теплоемкость газа при условии постоянного объема, то есть \(c_{V}\).

Нагреть газ на 1 К в условиях постоянного давления можно, если потратить большее количество теплоты, чем при нагревании газа на 1 К при стабильном объеме. Таким образом:

\(c_{P}>c_{V}\)

Если тело получает тепло в процессе нагрева или отдает тепло, охлаждаясь, то определить количество этой теплоты можно с помощью формулы:

\(Q=c*m(T_{2}-T_{1})\)\(Q=c*m(T_{2}-T_{1})\)

Где m является массой тела, c — представляет собой удельную теплоемкость, \(T_{2}\) — конечная температура тела, \(T_{1}\) — начальная температура тела.

Внутренняя энергия

Внутренняя энергия обозначается U. Единицей ее измерения в СИ является Дж (Джоуль).

В термодинамике внутренняя энергия определяется температурой и объемом тела. Данная величина находится в зависимости от таких параметров, как температура, масса и агрегатное состояние тела. При возрастании температуры внутренняя энергия увеличивается. Максимальная внутренняя энергия характерна для газообразного вещества, а наименьшая — для твердого вещества.

Внутренняя энергия идеального газа находится в прямо пропорциональной зависимости от его температуры. Данный параметр не зависит от объема по причине отсутствия взаимодействия молекул идеального газа между собой. Формула расчета внутренней энергии:

\(U=\frac{1}{2}v*R*T\)

Где i — является коэффициентом, равным количеству степеней свободы молекулы, ν — определяется, как количество вещества, R представляет собой универсальную газовую постоянную, T — является абсолютной температурой.

Число степеней свободы равно количество вероятных движений частиц.

Практические задачи по физике часто предполагают расчет изменения внутренней энергии, которое можно определить по формуле:

\(\Delta U=\frac{1}{2}v*R* \Delta T\)

\(\Delta T= T_{2}-T_{1}\)

С помощью уравнения Менделеева-Клапейрона формулу внутренней энергии можно упростить для решения задач:

\(U=\frac{1}{2}Pv\)

Где p — является давлением, V — представляет собой объем газа.

В случае реальных газов внутренняя энергия определяется и температурой, и объемом. Для изменения внутренней энергии необходимо изменить температуру путем теплопередачи, изменить давление и объем, совершая работу.

Работа в термодинамике

Работу обозначают, как \(A^{,}\). В СИ работу измеряют в Джоулях (Дж). Для обозначения работы внешних сил над газом используют А. Существует следующая закономерность:

\(A^{,}=-A\)

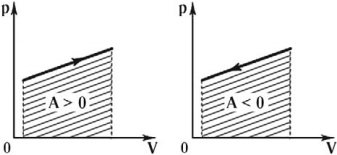
Работа расширения идеального газа представляет собой работу, совершаемую газом против внешнего давления. Работа газа обладает положительным значением в процессе расширения и отрицательным — при сжатии газообразного вещества. В том случае, когда объем газа стабилен, то есть наблюдается изохорный процесс, рассматриваемый газ не совершает работу.

Графическим способом работу газа можно определить в виде площади фигуры под графиком, отражающим зависимость давления от объема в координатных осях (p,V), ограниченная графиком, осью V и перпендикулярами, проведенными из точек начального и конечного значений объема.

Формулы для расчета работы газа отличаются в зависимости от условий:

• при изобарном процессе \(A^{,}=p*\Delta V\)
• в условиях изотермического процесса \(A^{,}=\frac{m}{M}RT\ln \frac{V_{2}}{V_{1}}\)

Энтропия

Энтропия определяется, как:

\(dS=\frac{\delta Q}{T}\)

Где \(\delta Q\) — количество теплоты, которое получает термодинамическая система при обратимом процессе; T — термодинамическая температура системы.

При условии любого обратимого кругового процесса изменение энтропии равно нулю:

\(\Delta S=0\)

При совершении энтропией системы необратимого цикла ее величина увеличивается:

\(\Delta S>0\)

Последние две записи справедливы только в случае замкнутых систем. Когда наблюдается тепловой обмен системы с внешней средой, поведение энтропии может быть любым. Рассматриваемые закономерности в комплексе являются неравенством Клаузиуса:

\(\Delta S\ge 0\)

Смысл данного выражения заключается в том, что при условии обратимых процессов в замкнутых системах наблюдается стабильность энтропии. Когда такие процессы необратимы, энтропия растет. При равновесном переходе из одного состояние в другое, согласно определения энтропии, справедливо следующее равенство:

\(\Delta S=S_2-S_1=\int^2_1{\frac{\delta Q}{T}=\int^2_1{\frac{dU+\delta A}{T}}}\)

В данном случае \(\delta Q=dU+\delta A\) , исходя из первого начала термодинамики. dU — является изменением внутренней энергии термодинамической системы. \(\delta A\) — представляет собой работу, которую выполняет система.

В записанном уравнении подынтегральное выражение и пределы интегрирования необходимо выразить с помощью параметров, характеризующих процесс, который протекает в термодинамической системе. Это выражение определяет энтропию с точностью до аддитивной постоянной. Физический смысл заключается в изменении энтропии, а не самой энтропии.

Энтропия характеризуется свойством аддитивности, то есть энтропия системы тел определяется, как сумма энтропий каждого тела, которое является компонентом системы. Ключевой тезис энтропии открывает статистическая физика. Больцманом было установлено связь энтропии системы с термодинамической вероятностью (W):

\(S=k\ ln\ W\)

Где k — постоянная Больцмана.

Известно, что термодинамическая вероятность представляет собой количество методов реализации макросостояния термодинамической системы, либо число микросостояний, которые реализуют данное макросостояние.

Энтропия представляет собой меру вероятности состояния термодинамической системы. В определенных случаях, согласно статистическому толкованию энтропии, ее определяют, как меру неупорядоченности системы.

Формы перехода энергии

Термодинамика изучает обобщенные закономерности и процессы преобразования энергии. При этом подразумевается наличие энергии у любого тела. Данная величина определяется температурой рассматриваемого тела:

\(U=\frac{i}{2}\frac{m}{\mu }RT\)

Где i — число степеней свободы молекулы; m — масса; \(\mu\) — молярная масса; \(R=8,31\ \frac{J}{mol\cdot K}\) —универсальная газовая постоянная; T — температура, относительно абсолютной шкалы.

В процессе теплового обмена теплота в количестве Q представляет собой меру, характеризующую изменение внутренней энергии. Количество теплоты, получаемой телом, которая обладает массой m, при росте его температуры на величину равную \(\Delta \ t (^{\circ}C)\), равно:

\(\Delta Q=mc\Delta \ t\)

Где \(c=\frac{C}{m}\) — удельная теплоемкость вещества.

В обобщенном варианте теплоемкость тела (C) определяется, как:

\(C=\frac{\delta Q}{dT}\)

Исходя из первого начала термодинамики, теплота, получаемая термодинамической системой \((\Delta Q)\), тратится ей на совершение работы (A) и изменение ее внутренней энергии \((\Delta U)\):

\(\Delta Q=A+\Delta U\)

Запись первого закона термодинамики при элементарном изменении состояния термодинамической системы имеет следующий вид:

\(\delta Q=\delta A+Du\)

\(CdT=pdV+dU\)

Где p — давление; dV — элементарное изменение объема.

Термодинамический коэффициент полезного действия \((КПД) (\eta)\) является отношением работы (A), совершаемой рабочим телом, к количеству теплоты \((Q^+)\), получаемому рассматриваемым телом:

\(\eta =\frac{A}{Q^+}=\frac{Q^+-Q^-}{Q^+}\)

Где \(Q^- \)— количество теплоты, которое рабочее тело передает холодильнику.

В случае цикла Карно, состоящего из пары изотерм и пары адиабат, который проводят с идеальным газом, КПД составляет:

\(\eta =\frac{T_1-T_2}{T_1}\)

Где \(T_1\) — температура нагревателя; \(T_2\) — температура холодильника.

Известны две формы передачи энергии от одних тел к другим:

• совершение работы одними телами над другими;
• теплопередача.

Возможен переход энергии механического движения в энергию теплового движения и обратный процесс. В процессе таких трансформаций энергии выполняется определенная закономерность, описывающая сохранение энергии. Применительно к термодинамическим процессам, закон сохранения энергии называют первым законом или первым началом термодинамики. Данная закономерность обобщает эмпирические данные. Согласно ему, количество теплоты, подводимое к системе, тратится на выполнение рассматриваемой системой работы, направленной против внешних сил, и изменение ее внутренней энергии. Математическая формулировка закона имеет следующий вид:

\(\Delta Q=\Delta U+A\)

Где \(\Delta Q\) — количество теплоты, которое получает термодинамическая система; \(\Delta U\) — изменение внутренней энергии данной системы; A — работа, выполняемая системой над внешними телами против внешнего воздействия.

Дифференциальный вид закона:

\(\delta Q=dU+\delta A\)

Где \(\delta Q\) — элемент количества теплоты, который получает система; \(\delta A\) — бесконечно малая работа, выполняемая термодинамической системой; dU — элементарное изменение внутренней энергии данной системы.

Важным фактом является то, что в записанной формуле dU — является элементарным изменением внутренней энергии и представляет собой полный дифференциал, что отличает данный параметр от \(\delta Q\) и \(\delta A.\)

Количество теплоты является положительной величиной в том случае, когда в систему поступает тепло. Если термодинамическая система отдает тепло, то количество теплоты будет отрицательным. Работа, совершаемая системой, больше нуля. При отрицательном значении работы можно говорить о том, что она совершается над системой внешними силами.

При возврате системы в исходное состояние, изменение ее внутренней энергии обладает нулевым значением:

\(\Delta U=0\)

Таким образом, согласно первому закону термодинамики:

\(\Delta Q=A\)

Три начала термодинамики, формулы и примеры решения задач

Благодаря открытию закона сохранения энергии, стали активно развиваться исследования в области термодинамики. Термодинамика является количественной теорией тепловых процессов. Развитие этой научной области обязано совершенствованию техники и появлению первых тепловых двигателей.

Первая задача термодинамики заключалась в получении оптимальных условий использования теплоты в процессе совершения работы. Энергетический обмен в термодинамике описывают с помощью понятий и величин, которые по смыслу не связаны со знаниями о микромире. Такие параметры являются макроскопическими. Они применимы только в случае макроскопических тел.

Достоинства термодинамического метода:

• термодинамические методы и соотношения не изменяются при развитии или даже принципиальном изменении представлений о строении вещества;
• применимость к веществам в любом состоянии, включая газообразное, твердое, жидкое, электромагнитное излучение.

Недостатки термодинамического метода:

• требуется информация о свойствах вещества при использовании обобщенных соотношений термодинамики;
• необходимость в опытном изучении каждого отдельно взятого вещества.

Первым началом термодинамики является применение закона сохранения энергии к процессам, рассматриваемым с точки зрения термодинамики, то есть тепловым явлениям. Интегральный вид закона сохранения энергии для теплоты, которая является формой энергии (\(\Delta Q\)), внутренней энергии (\(\Delta U\)) и работы (A), совершаемой термодинамической системой:

\(\Delta Q=A+\Delta U\)

Смысл данной закономерности заключается в том, что количество теплоты, которое подводят к термодинамической системе, тратится на совершение этой системой работы и изменение ее внутренней энергии. Условно считают, что, в случае подведения теплоты к системе, ее значение больше нуля (\(\Delta Q>0\)), и, когда работа выполняется самой системой, она положительна (A>0).

Дифференциальный вид первого начала термодинамики:

\(\delta Q=\delta A+Du\)

Где \(\delta Q\) — бесконечно малое количество теплоты, получаемой системой; \(\delta A\) — элементарная работа, которую выполняет термодинамическая система; dU — малое изменение внутренней энергии системы.

Второе начало определяет направление развития процессов, исследуемых термодинамикой. Исходя из рассматриваемой закономерности, исключается полное превращение теплоты в работу. Существует несколько определений второго начала термодинамики. Одна из них сформулирована, следующим образом: при любом процессе, который происходит в замкнутой системе, энтропия не убывает. Формула второго закона термодинамики:

\(\int^{\left(1\right)}_{ \begin{array}{c} \left(2\right) \\ L \end{array} }{\frac{\delta Q}{T}=\int^{(1)}_{(2)}{dS}}=S_1-S_2\le 0\)

Где S — энтропия; L — путь, по которому система переходит из одного состояния в другое. Записанное определение второго закона термодинамики сформулировано на основании понятия энтропии, которое используют в качестве функции состояния термодинамической системы.

Применяя третье начало термодинамики, можно ограничить процессы. Согласно закону, не существует процессов, в результате которых был бы достигнут термодинамический нуль температуры.

Примеры решения задач

Задача 1

Необходимо записать первый закон термодинамики в интегральном виде для идеального газа. В первой ситуации наблюдается изохорный процесс, а во второй — изотермический.

Решение

Исходя из первого начала термодинамики, можно записать формулу:

\(\Delta Q=A+\Delta U\)

Изохорный процесс в идеальном газе характеризуется следующей закономерностью:

\(m=const; V=const\)

Где m — масса идеального газа; V — объем газа.

Работа газа в данном случае обладает нулевым значением. Таким образом:

\(\Delta Q=\Delta U=\frac{i}{2}\frac{m}{\mu }R\Delta T\)

Здесь изменение внутренней энергии идеального газа можно выразить, как:

\(\Delta U=\frac{i}{2}\frac{m}{\mu }R\Delta T\)

В рассматриваемой формуле i — количество степеней свободы молекулы идеального газа; \(\mu\) — молярная масса газа; R — универсальная газовая постоянная; \(\Delta T\) — изменение температуры газа в процессе.

Формула для изотермического процесса будет иметь следующий вид:

\(m=const; T=const\)

Внутренняя энергия в данном случае не изменяется. Таким образом:

\(\Delta Q=A\)

Формула для определения работы газа:

\(A=\int^{V_2}_{V_1}{pdV\ }\)

Уравнение Менделеева-Клапейрона:

\(pV=\frac{m}{\mu }RT\)

Далее следует выразить давление, чтобы рассчитать работу в условиях изотермического процесса в идеальном газе:

\(A=\int^{V_2}_{V_1}{\frac{m}{\mu }R\frac{T}{V}dV=}\frac{m}{\mu }RT{\ln \left(\frac{V_2}{V_1}\right)}\)

Таким образом, первый закон термодинамики в случае изотермического процесса имеет вид:

\(\Delta Q=\frac{m}{\mu }RT{ln \left(\frac{V_2}{V_1}\right)}\)

Ответ:

1. \(\Delta Q=\Delta U=\frac{i}{2}\frac{m}{\mu }R\Delta T.\)
2. \(\ \Delta Q=A=\frac{m}{\mu}RT{ln \left(\frac{V_2}{V_1}\right)}.\)

Задача 2

Требуется вычислить количество теплоты, сообщаемое идеальному газу, который имеет объем V, чтобы в процессе изохорного нагрева его давление изменилось на \(\Delta p. \)При этом число степеней свободы молекулы газа можно считать равным i.

Решение

В первую очередь следует записать формулу первого начала термодинамики:

\(\Delta Q=A+\Delta U\ \)

Исходя из условия задачи, процесс является изохорным, поэтому работа обладает нулевым значением. Таким образом, можно преобразовать записанную формулу:

\(\Delta Q=\Delta U\ \)

Внутренняя энергия идеального газа изменяется, согласно следующей закономерности:\(\Delta U=\frac{i}{2}\nu R\Delta T\ \)Описать состояние идеального газа можно, используя уравнение Менделеева-Клапейрона:

\(pV=\nu RT\)

С помощью уравнения, характеризующего начальное и конечное состояния газа в рассматриваемом процессе, можно определить, как изменяется температура (\(\Delta T\)):\(p_1V=\nu RT_1; \ p_2V=\nu RT_2\to \Delta T=\frac{\Delta pV}{\nu R} \)В результате получим:

\(\Delta Q=\frac{i}{2}\Delta pV\ \)

Ответ: \(\Delta Q=\frac{i}{2}\Delta pV\)

Задача 3

В условиях протекания изохорного процесса к идеальному газу подвели определенное количество теплоты. Работа газа при этом равна А. Число степеней свободы молекулы газа можно принять за i. Требуется вычислить количество теплоты.

Решение

Исходя из первого закона термодинамики, можно записать формулу в интегральном виде:

\(\Delta Q=A+\Delta U\)

Внутренняя энергия изменяется, независимо от процесса:

\(\Delta U=\frac{i}{2}\nu R\Delta T\)

Согласно определению, работа равна:

\(A=\int^{V_2}_{V_1}{pdV}\)

По условиям задачи ситуация происходит при изобарном процессе. Таким образом:

\(A=p\Delta V\)

Уравнение Менделеева-Клапейрона поможет описать состояние, в котором находится идеальный газ:

\(pV=\nu RT\)

Далее следует записать уравнение, характеризующее начальное и конечное состояния газа, чтобы найти параметр \((p\Delta V):\)

\({pV}_1=\nu RT_1; \ {pV}_2=\nu RT_2\to p\Delta V=\nu R\Delta T=A\)

После сравнения записанных выражений получим:

\(\Delta U=\frac{i}{2}A\)

Таким образом, формула первого начала термодинамики будет преобразована, что позволит найти количество теплоты, которое было подведено в рассматриваемом процессе:

\(\Delta Q=A+\frac{i}{2}A=\frac{i+2}{2}A \)

Ответ: \(\Delta Q=\frac{i+2}{2}A\)

Задача 4

В процессе адиабатного расширения \(\nu\) моль кислорода увеличил свой объем в n раз. Требуется определить, как изменилась внутренняя энергия газа (\(\Delta U\)). При этом исходный объем газа равен \(V_1\), а температура \(T_1.\) Кислород можно принять за идеальный газ.

Решение

В случае идеального газа внутренняя энергия изменяется, таким образом:

\(\Delta U=\frac{i}{2}\nu R\Delta T=\frac{i}{2}\nu R(T_2-T_1)\)

Где \(\nu =\frac{m}{\mu }.\)

Когда указанный в условии задачи га является кислородом, то можно считать i известной величиной.

Так как наблюдается ситуация адиабатного расширения, следует записать его уравнение:

\(T_1V^{\gamma -1}_1=T_2V^{\gamma -1}_2\)

Где показатель адиабаты \(\gamma =\frac{i+2}{i}.\)

Далее нужно определить \(T_2\):

\(T_2=T_1{\left(\frac{V_1}{V_2}\right)}^{\gamma -1}\)

Затем необходимо подставить определенную температуру \(T_2\) в первое уравнение:

\(\Delta U=\frac{i}{2}\nu RT_1\left({\left(\frac{V_1}{V_2}\right)}^{\gamma -1}-1\right)=\frac{i}{2}\nu RT_1(n^{1-\gamma }-1)\)

Ответ: \(\Delta U=\frac{i}{2}\nu RT_1(n^{1-\gamma }-1)\)

Задача 5

Идеальный газ выполняет цикл Карно. КПД цикла составляет \(\eta\). В процессе изотермического расширения (1-2) газ совершает работу \(A_{12}\). Требуется определить работу изотермического сжатия (3-4).

Решение           

Идеальный га получает тепло в процессе 1-2, в процессе 3-4 тепло высвобождается. КПД цикла определяется по формуле:

\(\eta =\frac{A}{Q_1}=\frac{Q_1-Q_2}{Q_1}\)

Вычислить работу А можно, таким образом:

\(A=A_{12}+A_{34}=\eta A_{12}\)

Далее можно записать уравнение для работы изотермического сжатия:

\(A_{34}=\left(\eta -1\right)A_{12}\)

Ответ: \(A_{34}=\left(\eta -1\right)A_{12}\)

Задача 6

Требуется представить параметры простых изопроцессов, которые протекают в идеальном газе, сформулировать закономерности, которые определяют параметры их состояний. Также необходимо записать первое начало термодинамики применительно к данным процессам.

Решение

Характеристики изохорного процесса:

\(m=const;\ V=const.\)

Взаимосвязь параметров состояния процесса описывает закономерность Шарля:

\(\frac{p}{T}=const\ \)

При изохорном процессе работа обладает нулевым значением:

\(A=0;\ \delta A=0\)

Можно записать первое начало термодинамики для изохорного процесса:

\(\Delta Q=\Delta U=C_V\Delta T;\ \delta Q=C_VdT\ \)

Характеристики изобарного процесса следующие:

\(m=const;\ p=const.\)

Связать параметры состояния изобарного процесса можно с помощью закона Гей-Люссака:

\(\frac{V}{T}=const\ \)

Работа в случае изобарного процесса определяется, таким образом:

\(A=p\Delta V;\ \delta A=pdV\ \)

Первое начало термодинамики, когда наблюдается изобарный процесс:

\(\Delta Q=A+\Delta U=C_p\Delta T;\ \delta Q=C_pdT\ \)

Характеристики изотермического процесса:

\(m=const;\ T=const.\)

Описать параметры состояния изотермического процесса можно с помощью закона Бойля-Мариотта:

\(pV=const\ \)

В случае изотермического процесса работа будет определена, таким образом:

\(\delta A=pdV;\ A=\nu RTln(\frac{V_2}{V_1})\)

При изотермическом процессе внутренняя энергия не изменяется. Исходя из этого, формула для первого начала термодинамики будет иметь следующий вид:

\(\Delta Q=A;\ \delta Q=\delta A\)

Задача 7

Идеальному газу передано количество теплоты (\(\Delta Q\)). Рассматриваемый газ обладает объемом V и находится в состоянии изохорного процесса. Рост давления газа соответствует величине \(\Delta p\). Число степеней свободы молекулы газа равно i. Требуется определить количество теплоты (\(\Delta Q\)).

Решение           

Начинать решение данной задачи следует с записи первого закона термодинамики в интегральном виде:

\(\Delta Q=\Delta U+A\)

Согласно условиям задачи, наблюдается изохорный процесс (V=const). В этом случае работа равна нулю. Таким образом, уравнение первого начало термодинамики можно преобразовать:

\(\Delta Q=\Delta U\)

Определить, как изменилась внутренняя энергия, можно с помощью формулы:

\(\Delta U=\frac{i}{2}\nu R\Delta T\)

Где i — число степеней свободы молекулы газа; \(\nu\) — количество вещества; R — универсальная газовая постоянная.

При неизвестном параметре изменения температуры газа следует воспользоваться уравнением Менделеева-Клапейрона, чтобы вычислить \(\Delta T:\)

\(pV={\mathbf \nu }RT\)

Далее нужно выразить температуру и записать уравнения для двух состояний рассматриваемой системы:

\(T=\frac{pV}{\nu R}\to T_1=\frac{p_1V}{\nu R};\ \ T_2=\frac{p_2V}{\nu R}\)

Затем можно рассчитать \(\Delta T=T_2-T_1:\)

\(\Delta T=\frac{p_2V}{ \nu R}-\frac{p_1V}{ \nu R}=\frac{V}{ \nu R}\left(p_2-p_1\right)=\frac{V}{ \nu R}\Delta p\)

Таким образом, при изохорном процессе внутренняя энергия будет изменяться:

\(\Delta U=\frac{i}{2}\nu R\cdot \frac{V}{\nu R}\Delta p=\frac{i}{2}V\Delta p\)

Так как по первому началу термодинамики для изохорного процесса V=const, можно записать уравнение:

\(Delta Q=\frac{i}{2}V \Delta p\)

Ответ: \(\Delta Q=\frac{i}{2}V \Delta p\)

Задача 8

Требуется определить, как изменялась внутренняя энергия кислорода (\(\Delta Q\)), какую работу он совершил (А), и какое количество теплоты (\(\Delta Q\)) было получено в процессах: процесс 2-3 происходит при постоянном объеме (является изохорным), процесс 1-2 протекает при постоянном давлении. Дано, что \(V_1=1\) м3; \(p_1= 100\) кПа; \(V_3=3\) м3; \(p_2=500\) кПа.

Решение

Внутренняя энергия изменяется, независимо от течения процесса, так как внутренняя энергия представляет собой функцию состояния. Данный параметр определяется только конечным и начальным состояниями системы. В связи с этим, внутренняя энергия будет изменяться, таким образом:

\(\Delta U=\frac{i}{2}\nu R\Delta T\)

Где i — число степеней свободы молекулы кислорода (так как молекула состоит из двух атомов, то считаем i=5), \(\nu\) — количество вещества, \(\Delta T=T_3-T_1.\)

Разность температур определяется с помощью уравнения состояния идеального газа:

\(pV={\mathbf \nu }RT\to T=\frac{pV}{\nu R}\to \Delta T=T_3-T_1=\frac{1}{\nu R}\left(p_2V_2-p_1V_1\right)\)

Далее следует преобразовать уравнение:

\(\Delta U=\frac{i}{2}\left(p_2V_2-p_1V_1\right)\)

Изменение внутренней энергии можно определить, как:

\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\Delta U=\frac{5}{2}\left(500\cdot {10}^3\cdot 3-200\cdot {10}^3\cdot 1\right)=3,25\cdot {10}^6(J)\)

Процесс 2-3 не сопровождается изменением объема газа, поэтому является изохорным, а работа при этом обладает нулевым значением. Процесс 1-2 характеризуется стабильным давлением, поэтому работу в этом случае можно вычислить, таким образом:

\(A=p_1\left(V_2-V_1\right)\)

Определить работу в процессе 1-2-3 с учетом \(V_2=V_3\) можно следующим способом:

\(A=200\cdot {10}^3\left(3-1\right)=4\cdot {10}^5\ (J)\)

Далее следует записать первое начало термодинамики в интегральном виде:

\(\Delta Q=\Delta U+A\)

Затем следует определить количество теплоты, полученное кислородом в процессе 1-2-3:

\(\Delta Q=3,25\cdot {10}^6+0,4\cdot {10}^6=3,65\cdot {10}^6(J)\)

Ответ: \(\Delta U=3,25\cdot {10}^6 Дж; A=0,4\cdot {10}^6 Дж; \Delta Q=3,65\cdot {10}^6\)\(Дж\)