Как перевести градусы в радианы

Градусы в радианы

Краткое описание

Угол — это два луча, выходящие из одной точки. Эта точка называется вершиной. Взяв за единицу измерения некий конкретный угол, можно определить величину любого угла, выяснив, сколько раз в нем укладывается такой единичный угол. При измерении угла исходят из двух его свойств:

1. Величины равных углов равны.
2. Величина суммы двух углов равна сумме их величин.

Если ясно, о чем идет речь, вместо «величина угла» говорят просто «угол».

Равные углы с вершиной в центре окружности будут создавать на ней дуги одинаковой длины. Их сумма будет равняться сумме стягиваемых ими дуг. Поэтому единицы измерения углов можно задавать, указывая, какую часть окружности составляет соответствующая дуга.

В чем можно измерять угол

Наиболее распространены две единицы измерения:

• градус, равный дуге в 1/360 всей окружности;
• радиан — центральный угол, высекающий дугу, равную радиусу окружности.

Существуют еще такие единицы измерения, как град, равный 1/100 прямого угла, оборот, равный полному кругу, тысячная — \(\frac1{2\mathrm\pi\;\times\;1000}\) и румб — 1/32 полной окружности.

Связь между градусами и радианами

Мера угла

На практике чаще всего используют градусы. Их обозначают знаком \(^\circ\;\).

1/60 градуса — минута, обозначаемая знаком '. Секунду обозначают знаком '', она составляет 1/3600 доли.

Математики и астрономы предпочитают пользоваться радианом, безразмерной величиной. Это удобнее при рассмотрении тригонометрических функций. Обозначение «рад» при этом обычно опускают. Радиан равен примерно \(57^\circ17'45''\).

Формула соотношения

Длина дуги, высекаемой углом в a радиан на окружности радиуса R, вычисляется умножением a на R, а для единичной окружности длина дуги и величина угла совпадают.

Так как радиус равен единице, длина единичной окружности будет равна \(2\mathrm\pi\).

Таким образом, связь радиан и градусов можно выразить формулой

\(1\;\mathrm{радиан}\;=\;\frac1{\left(2\mathrm\pi\right)}\;\mathrm{оборотов}\;=\;\frac{180}{\mathrm\pi}\;\mathrm{градусов}\;=\;\frac{200}{\mathrm\pi}\;\mathrm{градов}\)

Формулы перевода

Градусы в радианы

Осуществить переход от градусов к радианам можно по формуле

\(\mathrm х^\circ\;=\;\frac{\pi\;\times\;а\;рад}{180^\circ}\)

Радианы в градусы

\(а\;рад\;=\;х^\circ\;\times\;(\;\frac{\mathrm\pi}{180^\circ})\)

Таблица перевода градусов в радианы

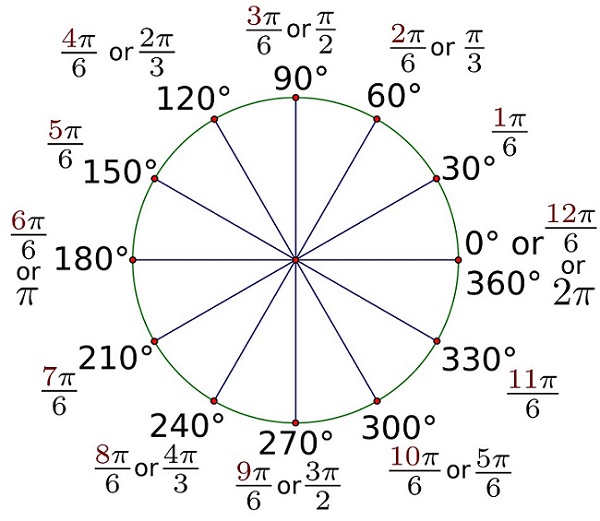
Соотношение двух систем измерения на окружности можно наглядно увидеть на схеме:

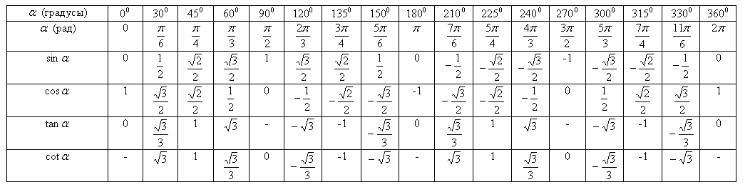
Но на практике, чтобы преобразовать одну величину измерения в другую, удобнее пользоваться таблицей:

Примеры расчета градусов и минут в радианы

Пример 1

Перевести 35 градусов в радианы.

Решение

Согласно формуле, нам нужно 35 умножить на число пи и разделить на 180.

\(х\;рад\;=\;35^\circ\;\times\;(\;\frac{\mathrm\pi}{180^\circ})\;\approx\;35^\circ\;\times\;(\;\frac{3,1416}{180^\circ})\;\approx\;0,6108\\35^\circ\;=\;0,6108\;рад\)

Чтобы выполнить перевод минут и секунд, нужно сначала перевести их в градусы.

Пример 2

Перевести в радианы угол \(87^\circ14'21''\).

Решение

\(1^\circ\;=\;60'\;=\;3600''\)

\(87^\circ+\;\frac{14'}{60}\;+\;\frac{21''}{3600}\;=\;87^\circ\;+\;0,2333^\circ\;+\;\;0,0058^\circ\;=\;87,239^\circ\)

Воспользуемся формулой, подставив найденное значение:

\(х\;рад\;=\;87,239^\circ\;\times\;(\;\frac{\mathrm\pi}{180^\circ})\;\approx\;87,239^\circ\;\times\;(\;\frac{3,1416}{180^\circ})\;\approx\;1,5226\\87,239^\circ\;=1,5226\;рад\)

Пример 3

Перевести в радианы угол \(194^\circ19'\).

Решение

\(1^\circ\;=\;60'\;=\;3600''\)

\(194^\circ+\;\frac{19'}{60}\;=\;194^\circ\;+\;0,3166^\circ\;=\;194,3166^\circ\)

\(х\;рад\;=\;194,3166^\circ\;\times\;(\;\frac{\mathrm\pi}{180^\circ})\;\approx\;194,3166^\circ\;\times\;(\;\frac{3,1416}{180^\circ})\;\approx\;3,3915\\194,3166^\circ\;=3,3915\;рад\)