Какой процесс называется изохорным

Какой процесс называется изохорным, условия протекания

Изохорный процесс можно наблюдать опытным путем. Для этого необходимо повышать или понижать температуру вещества в газообразном или жидком состоянии, находящегося в сосуде и сохраняющего стабильность объема. В случае, когда манипуляции производят с идеальным газом, его давление и температура будут изменяться прямо пропорционально, согласно закону Шарля. Для реальных газов данная закономерность не применима.

История возникновения теории, кто открыл, формула

Изучение изохорного процесса связывают с Гийомом Амонтоном. Работа ученого под названием «Парижские мемуары», написанная в 1702 году, посвящена исследованию характеристик газообразного вещества, помещенного в фиксированный объем, который составляет часть «воздушного термометра». Равновесие жидкости в данных условиях объясняется воздействием на нее давления газа, находящегося в сосуде, и атмосферного давления. Если температура среды повышается, показатели давления в резервуаре возрастают. При этом определенный объем жидкости вытесняется в выступающую трубку. Зависимость между такими характеристиками процесса, как температура и давление, представлена на рисунке.

В 1801 году были опубликованы два эссе исследователя Джона Дальтона с описанием эксперимента, результаты которого демонстрируют одинаковое расширение всех газов и паров при постоянном давлении и изменении температуры, когда начальная и конечная температура одинакова. В итоге был сформулирован закон Гей-Люссака. Ученый, в честь которого явление получило название, экспериментальным путем подтвердил одинаковое расширение различных газообразных веществ и вывел коэффициент, практически равный коэффициенту, полученному Дальтоном. Благодаря объединению данной закономерности с законом Бойля-Мариотта, был описан изохорный процесс.

График изохорного процесса в идеальном газе

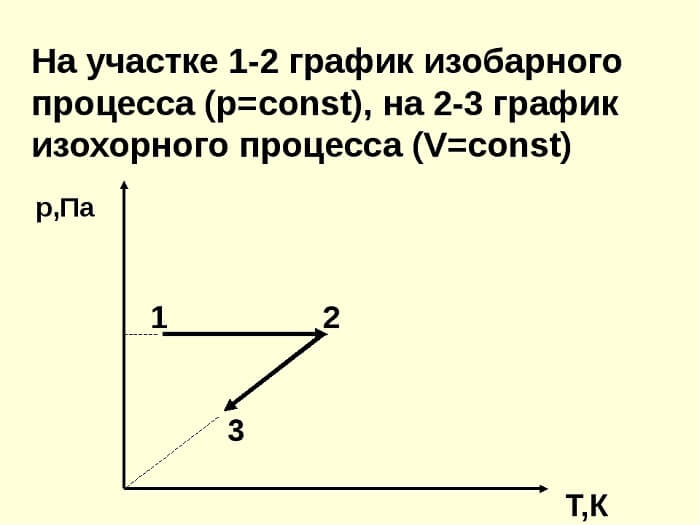
Зависимость характеристик при изохорном процессе можно представить схематично. График на диаграмме в системе координат будет иметь следующий вид:

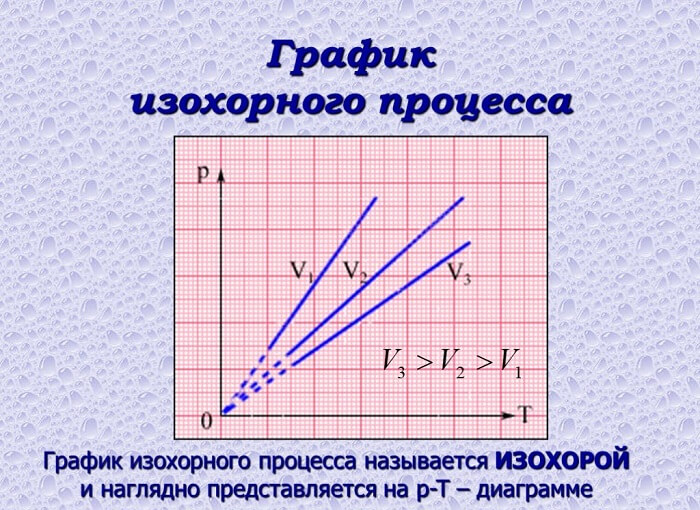
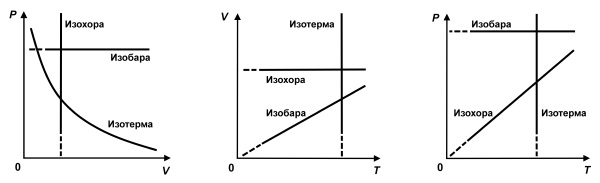
В случае идеального газа графически изохорные процессы будут изображены следующим образом:

Первый закон термодинамики для изохорного процесса

В условиях термодинамического процесса формула элементарной работы имеет следующий вид:

\(\delta A=PdV\)

Преобразование данного выражения позволит рассчитать величину полной работы процесса:

\(A=\int_{V_{1}}^{V_{1}}{PdV}\)

В случае, когда объем сохраняет  стабильность, то есть \(dV=0\), значение интеграла будет нулевым. Исходя из этого, в изохорном процессе работа газа не наблюдается:

\(A=0\)

Изменение внутренней энергии для идеального газа рассчитывается по формуле:

\(\Delta U=\frac{i}{2}\nu R\Delta T\)

где i представляет собой количество степеней свободы, зависящее от числа атомов, которыми обладает молекула газа. В качестве примера можно рассмотреть такие вещества:

• одноатомная молекула неона обладает тремя степенями;
• пять степеней характерно для двухатомной молекулы кислорода;
• в молекуле с тремя и более атомами, как у водяного пара, насчитывается 6 степеней.

Формула внутренней энергии выходит из понятия и уравнения теплоемкости, представляет собой следующее отношение:

\(\Delta U=\nu c_{\upsilon }^{\mu }\Delta T\)

где \(c_{\upsilon }^{\mu }\) является молярной теплоемкостью в условиях постоянного объема.

Расчет количества теплоты выполняют с помощью первого начала термодинамики в условиях термодинамического процесса:

\(Q=\Delta U+A\)

Следует учитывать, что в условиях изохорного процесса газообразное вещество не выполняет работу. Исходя из этого, можно вывести формулу:

\(Q=\Delta U=\nu c_{\upsilon }^{\mu }\Delta T\)

Согласно уравнению, газ получает теплоту. Она полностью расходуется, чтобы изменять внутреннюю энергию газообразного вещества.

Изменения термодинамических параметров в изохорном процессе

В условиях изохорного процесса наблюдается теплообмен с внешней средой. Данное явление называют изменением энтропии. Из его понятия следует уравнение:

\(dS=\frac{\delta Q}{T}\)

где \(\delta Q\) является элементарным количеством теплоты.

Преобразуя уравнение для расчета количества теплоты в дифференциальный вид, получают следующую формулу:

\(\delta Q=\nu c^{\mu }_{\upsilon }dT\)

где \(\nu\) является количеством вещества, а \(\nu c^{\mu }_{\upsilon }\)  обозначает молярную теплоемкость в условиях постоянного объема.

Формула микроскопического изменения энтропии в условиях протекания изохорного процесса имеет вид:

\(dS=\frac{\nu c^{\mu }_{\upsilon }dT}{T}dy/dx dy/dx\)

Если проинтегрировать последнюю формулу, то расчет полного изменения энтропии выполняют таким образом:

\(\int_{S_{1}}^{S_{2}}{dS}=\nu \int_{T_{1}}^{T_{2}}\frac{c^{\mu }_{\upsilon }dT}{T}\Rightarrow \Delta S=\nu \int_{T_{1}}^{T_{2}}\frac{c^{\mu }_{\upsilon }dT}{T}\)

В этой ситуации не представляется возможным вынести определение молярной теплоемкости в условиях стабильного объема за интеграл, так как оно представлено в виде функции, зависящей от температуры.

Применение эффекта изохорного процесса

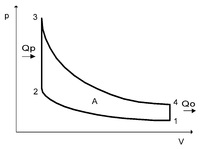
Идеальный цикл Отто приближенно воспроизведен в конструкции мотора внутреннего сгорания, работающего на бензине. Такты 2-3 и 4-1 при его функционировании представляют собой изохорные процессы. На выходе двигателя совершается работа. Она рассчитывается, как разность работ. К одной из них относят работу, производимую газообразным веществом над поршнем в процессе третьего такта или рабочего хода, к другой – работу, затраченную поршнем во время сжатия газа при втором такте. Таким образом, на примере двигателя, функционирующего, согласно принципу Отто, в системе принудительного сжигания смеси, газообразное вещество сжимается до 7-12 раз.

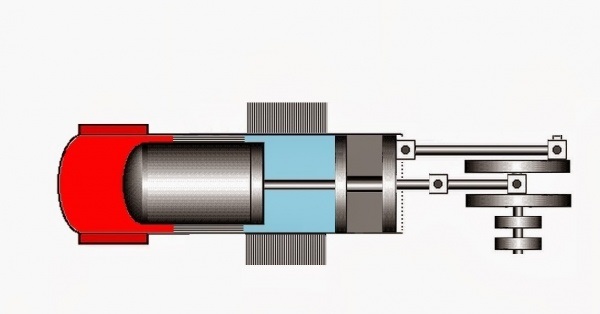
На рисунке изображен классический двигатель Стирлинга с конструкцией бета-типа, для которой характерно расположение рабочего и вытеснительного поршня в одном цилиндре.

Динамику цикла Отто можно представить в следующем виде:

Цикл Стирлинга также характеризуется наличием двух изохорных тактов. Процесс протекает при дооснащении конструкции двигателя Стирлинга регенератором. Во время прохождения газообразного вещества в одном направлении через наполнитель осуществляется передача тепла от рабочего тела к регенератору. Если газ проходит в обратную сторону, то тепловая энергия передается на рабочее тело. Идеальный цикл Стирлинга достигает обратимости и характеризуется теми же параметрами КПД, что и цикл Карно.