Кинематика вращательного движения твердого тела
Что такое кинематика вращательного движения
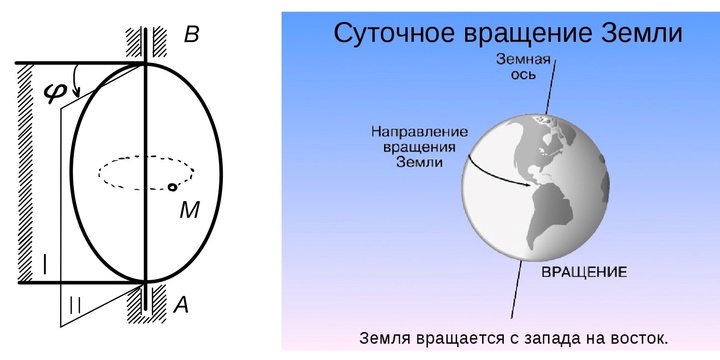
Вращательное движение — это вид движения, при котором все точки жесткого тела находятся на постоянном расстоянии от воображаемой оси и вращаются по кругу вокруг общей оси с общей скоростью.
Источник: surdoportal.guimc.bmstu.ru
Примеры:
- Футбольный мяч, вращающийся по своей траектории.
- Движение Земли вокруг оси.
- Вращение субатомных частиц в циклотроне.
- Гончарный круг, вращающийся вокруг своего центра.
- Конькобежец, демонстрирующий вращение во время своего выступления.
- Колесо, скатывающееся с холма.
- Вращающийся вокруг штифта проигрыватель фонографа.
Далее также описаны примеры вращательного движения, хотя на первый взгляд они таковыми не являются. Причина в том, что угол, на который вращаются объекты, невелик и не завершает полный круг:
- Дети играют на качелях.
- Поворот гаечного ключа.
- Открытие двери.
- Маятник, качающийся вокруг своей точки опоры.
Находит широкое применение в различных областях, в том числе:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
- Биомеханика: В человеческом теле суставы и мышцы опираются на вращательное движение. Понимание механики вращения помогает понимать движения и силы, возникающие при сочленении суставов, это позволяет продвинуться в протезировании и реабилитации.
- Машиностроение: анализа механических систем, таких как турбины, двигатели и редукторы. Оно помогает инженерам оптимизировать эффективность механизмов.
- Спорт: гимнастика, фигурное катание и прыжки в воду имеют сложные элементы. Для выполнения сложных маневров спортсмены используют принципы углового момента и вращательного момента.
- Астрономия: играет важную роль в изучении небесных тел, объясняет вращение планет, образование галактик и поведение звезд. Помогает ученым понять такие явления, как прецессия и нутация.
Отличие от кинематики поступательного движения
Любое тело одновременно может совершать поступательное и вращательное движение.
Поступательное движение — движение, при котором все точки движущегося тела перемещаются равномерно по одной линии или в одном направлении.
Если объект совершает поступательное движение, то при этом не происходит изменения его ориентации относительно неподвижной точки. Например, поезд движется по рельсам, человек идет по дороге, птицы летят в небе и т.д.
Когда тело смещается или перемещается из одной точки в другую, говорят, что тело испытывает поступательное движение. Значит все точки движущегося тела перемещаются равномерно по одной и той же линии или в одном и том же направлении. Если объект совершает поступательное движение, то при этом не происходит изменения его ориентации относительно неподвижной точки.
Таблица отличий:
| Категория | Вращательное движение | Поступательное движение |
| Определение | Объект, движущийся по фиксированной орбите по кругу, называется вращающимся. | Движение всех точек движущегося тела в одном направлении или по одной линии называется поступательным движением. |
| Формула для ускорения |
a = dω/dt, Где, a= ускорение, ω= угловая скорость, t= время. |
a = dv/dt,
Где, a= ускорение, v= скорость, t= время. |
| Описание движения | Поскольку вращательное движение не является линейным, оно может быть описано двумя параметрами — осью вращения и углом поворота. | Поскольку поступательное движение является линейным движением, оно может быть описано двумя параметрами — расстоянием и направлением. |
| Свойство ускорения | Как правило, неравномерно (из-за того, что центростремительное ускорение в каждый момент времени изменяется). | Может быть равномерным или неравномерным. |
Элементы кинематики вращательного движения
- Угловая скорость представляет собой скорость вращения объекта.
- Под угловым ускорением понимается скорость изменения угловой скорости объекта с течением времени.
- Угловое смещение измеряет изменение ориентации объекта при его вращении.
- Сохранение углового момента: Угловой момент сохраняется в замкнутой системе без внешнего вращающего момента. Этот принцип имеет множество применений, например, объясняет поведение вращающихся конькобежцев или сохранение углового момента у небесных тел.
- Свойство объекта, измеряющее его сопротивление изменению вращательного движения, называется моментом инерции. Он зависит от распределения массы и оси вращения объекта. Объекты с большим моментом инерции требуют большего крутящего момента для создания того же углового ускорения.
- Крутящий момент — это вращательный эквивалент силы. Он представляет собой силу, приложенную к объекту на расстоянии от оси вращения.
Основные уравнения и формулы
При изучении систем частиц и вращательного движения используется несколько формул. К числу наиболее важных формул относятся:
Центр масс
Формула для центра масс системы частиц имеет вид:
Rсм = (m1r1 + m2r2 + ... + mnrn) / (m1 + m2 + ... + mn),
где Rсм — вектор положения центра масс, m1, m2, ..., mn — массы частиц, r1, r2, ..., rn — векторы положения частиц.
Линейная кинетическая энергия
Формула для линейной кинетической энергии системы частиц имеет вид:
T = (1/2)m1v12 + (1/2)m2v22 + ... + (1/2)mnvn2
где
T — линейная кинетическая энергия системы,
m1, m2, ..., mn — массы частиц,
v1, v2, ..., vn — векторы скоростей частиц.
Крутящий момент
Представляет собой эффективность вращения силы. Например, для управления каруселью мы его применяем. Задается следующим уравнением:
τ=rFcosθ
Где
τ: крутящий момент
F: приложенная сила
r: Расстояние приложенной силы от оси вращения или длина плеча рычага
θ: Угол поворота
Единицей силы является ньютон N, а единицей расстояния — метр m. Таким образом, единицей крутящего момента является ньютон-метр или N-m.
Второй закон Ньютона для вращательного движения гласит, что любой объект будет двигаться с постоянной угловой скоростью, если на него не действует вращающий момент.
Импульс
Приведена формула для импульса системы частиц:
P = m1v1 + m2v2 + ... + mnvn
где,
P - линейный импульс системы,
m1, m2, ..., mn — массы частиц,
v1, v2, ..., vn — векторы скоростей частиц.
Угол поворота
Угол поворота объекта, вращающегося вокруг оси, определяется углом поворота θ. Он аналогичен расстоянию при линейном движении. Он показывает, насколько сильно вращается объект. Это переменная, зависящая от времени и удобная для измерения. Ее единицей является градус или радиан. Когда объект совершает один оборот, угол, который он описывает, равен 360˚ или 2π радиан.
Угловая скорость
Угловая скорость ω определяется как скорость вращения объекта. Она аналогична линейной скорости. Она определяется как изменение угла поворота, деленное на изменение времени.
ω=Δθ/Δt
Его единица измерения — радиан в секунду или рад/с.
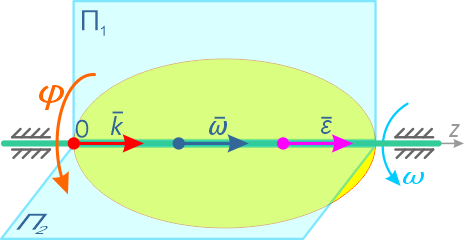
Тело вокруг относительно неподвижной оси и плоскость П (воображаемая)
Источник: isopromat.ru
Тангенциальная скорость и тангенциальное ускорение
Вращающийся объект также имеет тангенциальную скорость и тангенциальное ускорение. Тангенциальная скорость — мгновенная линейная скорость объекта. Связь между тангенциальной скоростью v и угловой скоростью ω имеет следующий вид:
v=ωr
Это уравнение говорит о том, что тангенциальная скорость v пропорциональна расстоянию r от центра вращения. Рассмотрим объект, вращающийся вокруг своей оси, проходящей через центр, например, компакт-диск. Точка, расположенная ближе к центру, будет иметь меньшую тангенциальную скорость, чем удаленная точка. Удаленная точка одновременно с ближайшей точкой совершает дугу большей длины. Обе эти точки будут иметь одинаковую угловую скорость.
Скорость изменения тангенциальной скорости дает тангенциальное ускорение a. Связь между тангенциальным ускорением и угловым ускорением следующая:
α=a/r
Величины тангенциального и углового ускорений прямо пропорциональны друг другу. Чем больше угловое ускорение, тем больше тангенциальное ускорение при условии, что радиус объекта остается постоянным.
Примеры решения задач
Рассчитать крутящий момент, если приложить силу 8 Н на расстоянии 2 м от оси вращения, перпендикулярно плечу рычага?
Решение:
F = 8 Н
r = 2 м
θ = 0˚
Определяем по формуле:
τ = r F cos θ
или, τ = 2 м * 8 Н * cos 0
или, τ = 16 Н-м.
Система из трех частиц с массами m1 = 3 кг, m2 = 4 кг и m3 = 5 кг находится в положениях r1 = (2, 3, 0), r2 = (4, 0, 0) и r3 = (0, 4, 0) соответственно. Найдите положение центра масс.
Решение:
Положение центра масс можно найти по формуле,
Rсм = (m1r1 + m2r2 + m3r3) / (m1 + m2 + m3)
Rсм = (3(2, 3, 0) + 4(4, 0, 0) + 5(0, 4, 0)) / (3 + 4 + 5)
Rсм = (6, 9, 0) / 12
Rсм = (1/2, 3/4, 0)
Таким образом, центр масс системы находится в точке (1/2, 3/4, 0).
Угловая скорость объекта изменяется от 5 рад/с по часовой стрелке до 10 рад/с по часовой стрелке за 4 с. Чему равно его угловое ускорение?
Решение:
ω1 = 5 рад/с
ω2 = 10 рад/с
t = 4 с
Угловое ускорение определяется следующим образом
α = (ω2 - ω1)/t
или, α = (10 рад/с - 5 рад/с)/4с
или, α = 1,25 рад/с.
Система из двух частиц с массами m1 = 2 кг и m2 = 3 кг вращается с угловыми скоростями ω1 = 2 рад/с и ω2 = 3 рад/с соответственно. Моменты инерции частиц равны I1 = 5 кг м2 и I2 = 7 кг м2. Найдите угловой момент системы.
Решение:
Угловой момент системы можно найти по формуле:
L = I1ω1 + I2ω2
L = 5(2) + 7(3)
L = 14
Таким образом, угловой момент системы равен 14 кг м2/с.
К частице, находящейся в положении r = (3, 4, 0) относительно оси вращения, приложена сила 10 Н. Найдите вращающий момент, действующий на частицу.
Решение:
Применим следующую формулу:
τ = r x F
τ = (3, 4, 0) x (0, 0, 10)
τ = (0, 0, -30) Н-м
Таким образом, вращающий момент на частице составляет (0, 0, -30) Н-м.
Балка длиной 140 см. На балку действуют три силы: F1 = 20 Н, F2 = 10 Н и F3 = 40 Н с направлением и положением. Какой крутящий момент вызывает вращение балки вокруг центра масс балки?
Дано:
Центр масс расположен в центре балки.
Длина балки (l) = 140 см = 1,4 метра
Сила 1 (F1) = 20 Н, плечо рычага 1 (l1) = 70 см = 0,7 метра
Сила 2 (F2) = 10 Н, плечо рычага 2 (l2) = 100 см - 70 см = 30 см = 0,3 метра
Сила 3 (F3) = 40 Н, плечо рычага 3 (l3) = 70 см = 0,7 метра
Решение :
Момент 1 вращает луч по часовой стрелке, поэтому моменту 1 присвоен отрицательный знак.
τ1 = F1 l1 = (20 Н)(0,7 м) = -14 Н м
Момент 2 вращает балку против часовой стрелки, поэтому моменту 2 присвоен положительный знак.
τ2 = F2 l2 = (10 Н)(0,3 м) = 3 Н м
Момент 3 вращает балку по часовой стрелке, поэтому моменту 3 присвоен положительный знак.
τ3 = F3 l3 = (40 Н)(0,7 м) = -28 Н м
Чистый момент :
Στ = -14 Нм + 3 Нм - 28 Нм = - 42 Нм + 3 Нм = -39 Нм
Величина момента равна 39 Н м. Направление вращения балки по часовой стрелке, поэтому ей присвоен отрицательный знак.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так