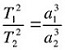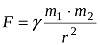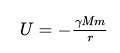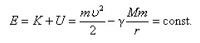Виды космических скоростей и чему они равны

Что такое космическая скорость и какой она бывает

Если подбросить какой-либо предмет вверх, то через некоторое время он вернется на земную поверхность. Одновременно с этим, спутник, запущенный в космос более полувека назад, космическая станция или Луна вращаются по определенным орбитам, как будто они не подвержены воздействию гравитационной силы притяжения нашей планеты.

Данному явлению есть научное объяснение. На Земле любое материальное тело испытывает на себе действие всемирного тяготения.Значит, должна существовать некая сила, обладающая способностью нейтрализовать гравитацию. Такая сила называется центробежной.

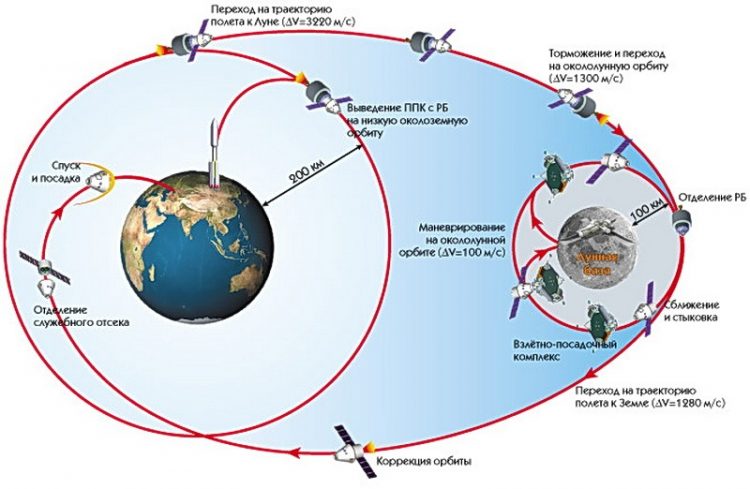
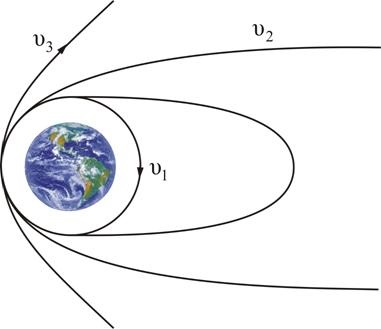
Действие центробежной силы можно почувствовать, если один конец нити соединить с небольшим грузом и раскрутить его по окружности. При увеличении скорости вращения усиливается натяжение нити. Если скорость вращения замедляется, то повышается вероятность того, что груз упадет на землю. На рисунке представлена траектория полета космических кораблей:

Исходя из рассмотренных примеров, можно представить формулировку понятия «космическая скорость». В упрощенной форме термин «космическая скорость» представляет собой такую скорость, которая позволяет некоему объекту преодолеть тяготение небесного тела и их системы.

С помощью космических скоростей характеризуют виды движения космического аппарата в сфере влияния небесных тел:

• Солнце;
• Земля;
• Луна;
• другие планеты и их естественные спутники;
• астероиды и кометы.

Все объекты, которые перемещаются по орбите, обладают космической скоростью. При этом космические объекты характеризуются определенными размерами и формами орбит, зависящими от величины и направления скорости, получаемой данным объектом при выключении двигателей, а также высоты, на которой произошло это отключение.

Сколько скоростей в астрономии, в чем измеряются

Исследователи еще в древние времена заметили, что по сравнению со звездами, неизменно сохраняющими свое взаимное расположение в пространстве на протяжение веков, планеты перемещаются около звезд по сложнейшим траекториям. Представил объяснение петлеобразного движения планет древнегреческий ученый К. Птолемей во II веке нашей эры.

Его предположение заключалось в том, что Земля расположена в центре Вселенной, а каждая из планет перемещается по малому кругу (эпициклу). Центр эпицикла, в свою очередь, равномерно движется по большому кругу, в центре которого находится Земля. Данная концептуальная теория получила название птолемеевой или геоцентрической системы мира.

В начале XVI столетия польский астроном Н. Коперник (1473 – 1543) обосновал гелиоцентрическую систему. Исходя из данной концепции, небесные тела движутся за счет движения Земли и других планет вокруг Солнца и суточного вращения нашей планеты.

В то время теорию наблюдения Коперника общество воспринимало в качестве занимательной фантазии. В XVI веке церковь выявила в этом утверждении ересь. По известным фактам Дж. Бруно, который открыто поддержал гелиоцентрическую систему Коперника, подвергся суду и был приговорен к казни путем сожжения на костре.

Несмотря на отсутствие поддержки в широких кругах, геоцентрическую систему мира в результате признало научное сообщество. Это произошло в начале XVII века, когда большинство ученых получили доказательства в пользу теории. Иоганн Кеплер путем обработки результатов многочисленных наблюдений, проведенных Тихо Браге, вывел закономерности, которым подчинены движения планет вокруг Солнца.

Ньютон открыл закон всемирного тяготения, основываясь на трех законах Кеплера.

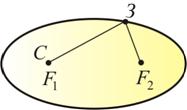
Первый закон Кеплера: все планеты движутся по эллипсам, в одном из фокусов которого находится Солнце.

Второй закон Кеплера: радиус-вектор планеты описывает в равные времена равные площади.

Третий закон Кеплера: квадраты времен обращения планет относятся как кубы больших полуосей их орбит.

Все планеты, за исключением Плутона, имеют орбиты движения, которые блики к круговым. В таком случае первый и второй законы Кеплера реализуются автоматически. Согласно третьему закону:

\(T^{2}\sim R^{3}\)

где Т – является периодом обращения;

R – радиус орбиты.

Ньютону удалось решить обратную задачу механики и с помощью законов движения планет получить формулу, выражающую гравитационную силу:

По известным данным, гравитационные силы представляют собой консервативные силы. В процессе движения тела в гравитационном поле консервативных сил по замкнутой траектории работа приобретает нулевое значение. Благодаря свойству консервативности гравитационных сил, было введено понятие потенциальной энергии. Таким образом, потенциальная энергия тела массы m, которое удалено от большого объекта массы М на расстояние r, равна:

В данном случае знак минуса демонстрирует тот факт, что гравитационные силы представляют собой силы притяжения. Когда тело помещено в гравитационное поле, удалено от центра тяготения на какое-то расстояние r и обладает некоторой скоростью v, его полная механическая энергия будет рассчитана по формуле:

Исходя из вышесказанного, можно сделать вывод о неизменности полной энергии тела в гравитационном поле, согласно закону сохранения энергии. Полная энергия может обладать положительным или отрицательным значением, либо иметь нулевое значение. От знака полной энергии зависит характер движения небесного тела.

В том случае, когда Е<0, тело не может удалиться от центра притяжения на расстояние \(r_{0}<r_{max}\). При этом небесное тело будет перемещаться по эллиптической орбите, как планеты Солнечной системы и кометы. Пример такого движения представлен на рисунке:

Период вращения небесного тела по эллиптической орбите соответствует периоду обращения по круговой орбите радиуса R, где R является большей полуосью орбиты. Если Е = 0, то тело будет перемещаться по параболической траектории. При этом тело обладает скоростью, равной на бесконечности нулю. Когда Е > 0, траектория движения тела представляет собой гиперболу. Объект будет удаляться на бесконечность с запасом кинетической энергии.

Таким образом, космическая скорость является минимальной скоростью, которую достаточно развить телу, чтобы преодолеть гравитацию того или иного объекта. Всего выделяют четыре вида космических скоростей:

• орбитальная;
• планетарная;
• звездная;
• галактическая.

Виды космических скоростей

Одним из первых понятие космических скоростей и метод определения их значений ввел российский ученый, который считается одним из пионеров современной космонавтики, Ари Абрамович Штернфельд. Термин «космическая скорость» был раскрыт им в книге «Введение в космонавтику» в 1934 году.

Космической скоростью является минимальная скорость, которой достаточно для того, чтобы тело, двигаясь свободно, могло:

• v1 — играть роль спутника небесного тела, то есть приобрести способность вращаться по орбите около небесного тела и не достигать его поверхности;
• v2 — преодолеть гравитационное притяжение небесного тела и начать движение по орбите в виде параболы;
• v3 — выйти в процессе запуска за пределы планеты, преодолев притяжение Звезды;
• v4 — при запуске из планетной системы выйти за пределы Галактики.

Космические скорости можно рассчитать при любом удалении от центра Земли. В космонавтике, как правило, используют величины, определенные конкретно для поверхности шаровой однородной земной модели, которая характеризуется радиусом в 6371 км.

Первая скорость

Таким образом, первая космическая скорость представляет собой минимальную скорость тела, при которой оно перемещается горизонтально над поверхностью планеты и не падает на нее, продолжая движение по круговой орбите. Для того, чтобы определить первую космическую скорость, следует рассмотреть равенство центробежной силы и силы тяготения, оказывающих воздействие на тело, перемещающееся по круговой орбите:

\(m\frac{v_{1}^{2}}{R}=G\frac{Mm}{R^{2}}\)

Таким образом:

\(v_{1}=\sqrt{G\frac{M}{R}}\)

где m – является массой объекта;

М – представляет собой массу планеты;

G — гравитационная постоянная;

\(v_{1}\) — первая космическая скорость.

Путем подстановки численных значений (для Земли M = 5,97·1024 кг, R = 6 378 км), найдем первую космическую скорость:

\(v_{1}\) = 7,9 км/с.

Первая космическая скорость может быть рассчитана с помощью ускорения свободного падения:

\(g=\frac{GM}{R^{2}}\)

\(v_{1}=\sqrt{gR}\)

Вторая скорость

Согласно предположениям, после того, как тело развивает вторую космическую скорость, оно не получает негравитационного ускорения. В таком случае двигатель должен быть отключен, а атмосфера – отсутствовать.

Определить вторую космическую скорость можно, зная радиус и массу небесного тела. В связи с этим, вторая космическая скорость рассчитывается конкретно для каждого небесного тела, то есть для каждой планеты, и представляет собой его характеристику:

• в случае Земли значение второй космической скорости составляет 11,2 км/с. Тело, двигающееся с такой скоростью вблизи нашей планеты, выходит за ее пределы и становится спутником Солнца;
• для Солнца вторая космическая скорость составляет 617,7 км/с;
• вторая космическая скорость для Луны равна 2,4 км/с, несмотря на то, что в действительности для удаления тела на бесконечность с поверхности Луны необходимо преодолеть притяжение Земли, Солнца и Галактики.

Получить формулу для ее расчета можно при определении скорости, которую объект приобретет на поверхности планеты, если будет приближаться к ней из бесконечности. Это именно такая скорость, которую требуется придать телу на поверхности планеты, чтобы оно покинуло пределы его гравитационного влияния. Таким образом:

\(\frac{mv_{2}^{2}}{2}=\frac{GMm}{R}\)

\(v_{2}=v_{1}\sqrt{2}\)

\(v_{2}=\sqrt{\frac{2GM}{R}}\)

В случае Земли вторая космическая скорость составит:

\(v_{2}\)=11,2 км/с

Третья скорость

Пилотируемые межзвездные путешествия могут осуществляться лишь с помощью космических кораблей, которым доступны третьи космические скорости. Таким образом, объекты могут достигнуть планетные системы других звезд. Стартуя с поверхности нашей планеты и максимально эффективно используя орбитальное движение Земли, космическому аппарату доступно достижение третьей космической скорости уже при 16,7 км/с по отношению к планете.

Если взлет с земной поверхности осуществляется в наиболее неблагоприятном направлении, то кораблю потребуется набрать скорость в 72,8 км/с. В данном случае расчет основан на предположении того, что искусственный космический аппарат данную скорость развивает, находясь непосредственно на поверхности нашей планеты, и не получает после этого негравитационное ускорение, то есть двигатели отключены, и сопротивление атмосферы отсутствует.

При учете притяжения других планет, что способствует ускорению или торможению аппарата, расширяется диапазон вероятных значений третьей космической скорости. Максимально энергетически выгодный старт предполагает одинаковые направления для скорости космического корабля и орбитального перемещения Земли вокруг Солнца. Орбита такого аппарата в Солнечной системе будет иметь вид параболы.

Четвертая скорость

Четвертая космическая скорость применяется достаточно редко, не отличается постоянством в разных точках Галактики и определяется расстоянием до центральной массы. В случае нашей Галактики центральной массой является объект Стрелец А, представленный сверхмассивной черной дырой.

По предварительным грубым расчетам четвертая скорость в районе нашего Солнца достигает 550 м/с. Данное значение определяется не только расстоянием от центра Галактики, но и распределением масс вещества по Галактике, о которых отсутствуют на данный момент точные сведения. Это связано с тем, что видимая материя составляет только небольшую часть от общего объема гравитирующей массы, а все остальное является скрытой массой.

В редких случаях в некоторых источниках упоминается термин «пятая космическая скорость». Понятие определяет скорость, которая необходима, чтобы объект достиг иной планеты звездной системы, независимо от разности плоскостей эклиптики планет. К примеру, в случае Солнечной системы, а именно, Земли, чтобы орбита межпланетного перелета была перпендикулярной к земной орбите, требуется скорость запуска 43,6 км/с.

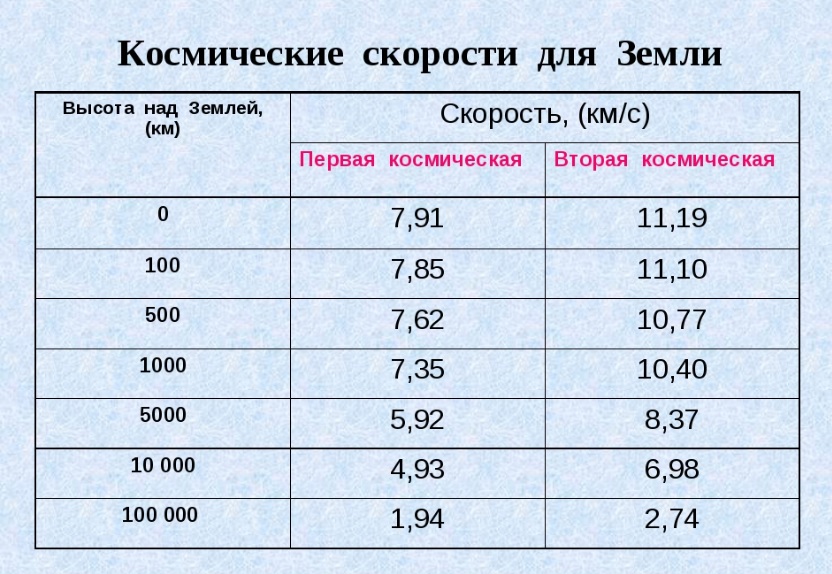
Таблица, космические скорости, рассчитанные для Земли

Космические скорости обладают прямой зависимостью от местных условий. В случае рассмотрения других космических объектов кроме нашей планеты, данные характеристики будет отличаться. Значения космических скоростей для Земли представлены в таблице: