Криволинейное движение: понятие, формулы, задачи
Что такое криволинейное движение
Наука механика охватывает множество разделов, в том числе, кинематику. Данное направление подразумевает изучение и описание разновидностей движения объектов. При этом силы, благодаря которым осуществляется такое перемещение, не учитывают. Одним из распространенных вопросов, интересных для рассмотрения, является передвижение тела, которое принимают за материальную точку, вдоль криволинейной траектории с определенным ускорением.
С помощью такой модели представляется возможным исследовать характер взаимодействия объектов и прогнозировать их поведение. В процессе изучения курса физики можно часто встретить вполне конкретизированное определение данного вида движения. Его смысл заключается в смене положения физической точки относительно пространства и прочих тел.
Известно, что какое-либо материальное тело включает в себя совокупность точек, которые передвигаются в одном направлении и темпе относительно друг друга. По этой причине любой объект допустимо принимать за простейшую точку. Это значительно упрощает процесс моделирования и изучения параметров его движения. Кроме того, с точки зрения кинематики интерес представляет путь перемещения точки, а не причины, формирующие то или иное движение.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Криволинейное движение представляет собой путь, который преодолела материальная точка, перемещаясь вдоль кривой траектории с каким-либо ускорением.
Аналогичным образом несложно сформулировать определение для прямолинейного движения. Под этим понятием имеется в виду процесс, когда материальная точка меняет собственное положение на прямой траектории. Заметим, что криволинейное передвижение осуществляется в любом случае ускоренно. Исходя из этого признака, целесообразно выделить несколько форматов подобного движения:
- Равномерное. Скорость передвижения по модулю не меняется в процессе преодоления расстояния. В качестве примера равномерного криволинейного движения можно привести перемещение по круговой траектории.
- Равноускоренное. В процессе движения такие параметры, как скорость и направление перемещения точки меняются. Ярким примером равноускоренного криволинейного движения является перемещение объекта, который подбросили под определенным углом к горизонту.
Нормальное и тангенциальное криволинейное движение
Ключевым параметром криволинейного движения является вектор перемещения. Для обозначения величины принято использовать букву S и дополнять ее стрелкой, то есть \(\overrightarrow{S}\). Перемещение в каком-либо случае ориентировано по хорде. Помимо этой характеристики, описывая криволинейное передвижение, принято оперировать понятиями тангенциального и нормального ускорения.
При тангенциальном ускорении движение по кривой траектории характеризуется сменой скорости за временной отрезок. Величина направлена так же, как скорость, либо ориентирована противоположно направлению скорости. При расчете тангенциального ускорения используют следующую формулу:
\(a_{t}=\frac{\lim \triangle v}{\triangle t}\)
В записанном выше математическом выражении v обозначает исходную скорость в момент времени \(t_{0} + \triangle t\).
Нормальное ускорение представляет собой параметр, описывающий криволинейное движение, и является перпендикуляром к направлению скорости. Вектор нормального ускорения совпадает с радиусом кривизны пути. Для вычисления нормального ускорения целесообразно использовать следующее математическое соотношение:
\(a_{n}=\frac{ v^{2}}{r}\)
Здесь r обозначает радиус, который имеет окружность. Разновидностью нормального ускорения является центростремительная сила. Этот параметр приобретает смысл и значение, когда рассматриваемое материальное тело перемещается по траектории, совпадающей с окружностью.
Источник: physics.shkolkovo.net
Исходя из вышесказанного, можно сформулировать заключение о том, что при криволинейном передвижении вектора скорости и ускорения не принадлежат одинаковой прямой. Наиболее примитивными примерами криволинейного движения, которые можно наблюдать в реальных жизненных условиях, служат течение воды по речной артерии, полет на самолете, катание на колесе обозрения.
Чему равно перемещение при криволинейном движении, формулы
Рассмотрим основные характеристики, которые помогут выполнить корректное описание и изучить криволинейное движение. Заметим, что при такой ситуации путь, то есть расстояние от точки начала до точки окончания передвижения, выраженное с помощью скалярной величины в виде какого-то числа, превышает по значению перемещение.
Источник: studall.org
Перемещением называют векторную величину, ключевыми характеристиками которой служат численное выражение, то есть модуль, и направление.
По мере удаления тела от начальной точки ее путь в любом случае увеличивается. При этом перемещение по модулю может прирастать или уменьшаться. Когда материальная точка вернулась в начало, можно говорить о нулевом значении величины перемещения. В то же время путь не равен нулю, а обладает каким-то значением.
Путь представляет собой скалярную величину с точки зрения физики, равную длине траектории, по которой перемещалось материальное тело в течение временного промежутка.
В процессе решения задач и представления моделей криволинейного передвижения тела необходимо принимать во внимание тот факт, что путь, обозначенный за S, всегда имеет положительное значение, то есть:
S > 0.
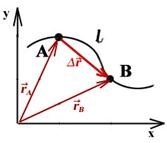
Представим, что материальное тело перемещается в течение какого-то временного отрезка из начальной точки в некую конечную точку, меняя собственное положение. Изобразим описанное движение на схеме:
Источник: studall.org
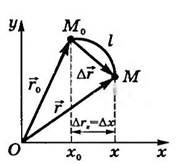
По изображению перемещения тела относительно начальной точки в плоскости координатных осей заметно, что радиус-векторы изменяются. С помощью этих величин можно определить положение тела в какой-либо временной момент t:
\(\overrightarrow{r}= \overrightarrow{r_{0}} + \triangle \overrightarrow{r}\)
\(\begin{cases}x = x_{0} + \triangle r_{x}\\y = y_{0} + \triangle r_{y}\end{cases}\)
Как направлен вектор скорости
Если в процессе движения по кривой траектории, ускорение материального тела стабильно и не меняется по значению, то целесообразно записать следующие формулы для характеристики скорости этого объекта:
\(v_{x} = v_{0x} + a_{x}t\)
\(x = x_{0} + v_{0x}t + \frac{a_{x}t^{2}}{2}\)
\(v_{y} = v_{0y} + a_{y}t\)
\(y = y_{0} + v_{0y}t + \frac{a_{y}t^{2}}{2}\)
В качестве частого случая перемещения тела по кривой траектории принято рассматривать движение объекта по окружности. При этом передвижение является равномерным с обязательным наличием какого-либо ускорения. Здесь скорость всегда направлена по касательной к траектории передвижения, а также регулярно изменяет собственное направление. По этой причине перемещение по окружности в любых случаях реализовано с центростремительным ускорением. Охарактеризовать рассмотренный случай можно с помощью математического выражения:
\(|\overrightarrow{a}| = \frac{v^{2}}{r}\)
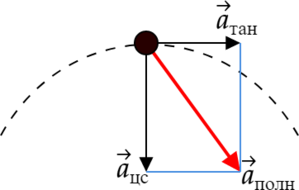
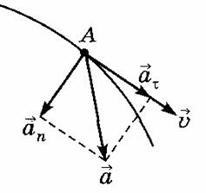
В записанной формуле r обозначает радиус, которым обладает окружность, описанная телом во время его передвижения. Ускорение ориентировано по направлению к центру круговой траектории и вычисляется, как сумма нормального и тангенциального ускорений. Ознакомиться с направлениями рассмотренных величин можно с помощью схематичного изображения криволинейного движения:
Источник: sfiz.ru
Примеры решения задач
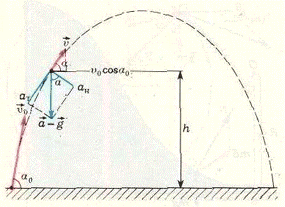
Находясь на горизонтальной поверхности земли, человек подбросил мяч под углом \({\alpha _0}\) относительно линии горизонта. Исходная скорость этого предмета составила \(\overrightarrow {{\upsilon _0}}\). Требуется вычислить, как взаимосвязаны тангенциальная и нормальная проекции ускорения объекта от высоты, на которую он поднялся в процессе своего движения. При выполнении расчетомв допустимо пренебречь величиной сопротивления воздушной среды, в которой происходит описанное движение.
Источник: easyfizika.ru
Решение
Рассмотрим подробнее условия задания. Согласно описанию движения после того, как мяч подбросили вверх, он испытывает на себе воздействие только одной силы. Этим действием обладает сила гравитации, то есть Земля притягивает тело. В таком случае в любой точке траектории ускорение \(\overrightarrow а\) тела равно ускорению свободного падения \(\overrightarrow g\). Тангенциальная и нормальная проекции ускорения равны, соответственно:
\({a_т} = g\sin \alpha \,\,{\text{и}}\,\,{a_н} = g\cos \alpha.\)
Здесь \(\alpha\) — угол, который составляет с горизонтом скорость \(\overrightarrow \upsilon\) тела на высоте h. Вспомним формулировку закона сохранения энергии и представим ее математическое выражение:
\(\frac{{m\upsilon _0^2}}{2} = \frac{{m{\upsilon ^2}}}{2} + mgh\)
И найдем выражение для модуля \(\upsilon\) скорости тела:
\(\upsilon = \sqrt {\upsilon _0^2 – 2gh}.\)
Во время движения проекция скорости на горизонтальное направление остается постоянной и равной \({\upsilon _0}\cos {\alpha _0}\). В таком случае получим следующее справедливое равенство:
\({a_н} = g\cos \alpha = g\frac{{{\upsilon _0}\cos {\alpha _0}}}{\upsilon } = g\frac{{{\upsilon _0}\cos {\alpha _0}}}{{\sqrt {\upsilon _0^2 – 2gh} }}\)
Кроме того, имеет смысл следующее математическое выражение для тангенциального ускорения:
\({a_т} = g\sin \alpha = g\sqrt {1 – {{\cos }^2}\alpha } = g\frac{{\sqrt {\upsilon _0^2{{\sin }^2}{\alpha _0} – 2gh} }}{{\sqrt {\upsilon _0^2 – 2gh} }}.\)
В полученные формулы можно ввести максимальную высоту подъема тела:
\({h_{\max }} = \frac{{\upsilon _0^2{{\sin }^2}{\alpha _0}}}{{2g}}\)
Таким образом:
\({a_н} = g\cos {\alpha _0}\frac{{\sqrt {{h_{\max }}} }}{{\sqrt {{h_{\max }} – h{{\sin }^2}{\alpha _0}} }}\)
\({a_т} = g\sin {\alpha _0}\frac{{\sqrt {{h_{\max }} – h} }}{{\sqrt {{h_{\max }} – h{{\sin }^2}{\alpha _0}} }}.\)
Ответ: \({a_н} = g\cos {\alpha _0}\frac{{\sqrt {{h_{\max }}} }}{{\sqrt {{h_{\max }} – h{{\sin }^2}{\alpha _0}} }}; {a_т} = g\sin {\alpha _0}\frac{{\sqrt {{h_{\max }} – h} }}{{\sqrt {{h_{\max }} – h{{\sin }^2}{\alpha _0}} }}.\)
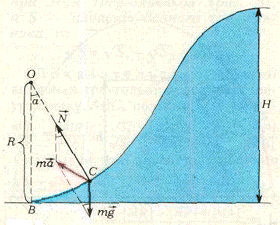
Заключительный фрагмент BC горного склона, где разгоняются лыжники, прыгая с трамплина, имеет дуговую форму некоторой окружности, радиус которой составляет R=15 м. Суммарная высота этой горы равна H=50 м. Нужно вычислить модуль ускорения лыжника в точке C, если угол \(\alpha = 15^\circ\). В процессе решения задачи допустимо принимать скорость спортсмена в начале пути за нулевую, а силу трения можно не учитывать.
Решение
В первую очередь необходимо проанализировать условия задания. В процессе передвижения по горному склону, готовясь к прыжку, спортсмен испытывает на себе воздействие внешних сил, а именно, тяжести и реакции опоры. Сила тяжести \(m\overrightarrow g\) ориентирована по вертикали вниз. Сила реакции опоры \(\overrightarrow N\) направлена при условии нулевого трения по радиусу кривизны траектории, то есть радиусу CO. Равнодействующая перечисленных сил придает спортсмену искомое ускорение \(\overrightarrow a\):
\(m\overrightarrow a = m\overrightarrow g + \overrightarrow N\)
Источник: easyfizika.ru
В процессе решения задач по кинематике нередко приходится иметь дело с громоздкими расчетами. На помощь в таких ситуациях приходят геометрические и тригонометрические закономерности. Применяя разнообразные соотношения величин из перечисленных наук можно значительно упростить решение примеров. Применительно к этой задаче целесообразно воспользоваться формулой, являющейся формулировкой теоремы косинусов. Тогда получим, что:
\({\left( {ma} \right)^2} = {\left( {mg} \right)^2} + {N^2} – 2mgN\cos \alpha .\)
Пусть \(\overrightarrow \upsilon\) является скоростью лыжника в точке C. Нормальная проекция ускорения составит:
\({a_н} = \frac{{{\upsilon ^2}}}{R}\)
Эта величина складывается из соответствующих проекций сил \(m\overrightarrow g и \overrightarrow N\):
\(\frac{{m{\upsilon ^2}}}{R} = N – mg\cos \alpha.\)
Исключая N из последних двух уравнений, получим:
\({a^2} = {g^2}{\sin ^2}\alpha + {\left( {\frac{{{\upsilon ^2}}}{R}} \right)^2}.\)
Заметим, что далее целесообразно прибегнуть к методу подстановки. Таким образом, возьмем модуль v скорости спортсмена из выражения, описывающего закономерность, согласно которой сохраняется энергия в замкнутой системе. В результате получим следующую запись:
\(\frac{{m{\upsilon ^2}}}{2} = mg\left( {H – R\left( {1 – \cos \alpha } \right)} \right)\)
Затем необходимо вычислить, чему равен модуль ускорения спортсмена:
\(a = \sqrt {{g^2}{{\sin }^2}\alpha + {{\left( {\frac{{{\upsilon ^2}}}{R}} \right)}^2}} = g\sqrt {{{\sin }^2}\alpha + 4{{\left( {\frac{H}{R} – 1 + \cos \alpha } \right)}^2}} \approx 65\;м/с^2.\)
Аналогичное значение достаточно просто вычислить другим способом. При перемещении вдоль дуги окружности нормальная проекция ускорения соответствует:
\({a_н} = \frac{{{\upsilon ^2}}}{R}\)
В этом же случае тангенциальная проекция, формируемая только соответствующей проекцией силы тяжести, вычисляется, как:
\({a_т} = g\sin \alpha\)
В таком случае модуль ускорения равен:
\(a = \sqrt {a_н^2 + a_т^2} = \sqrt {{g^2}{{\sin }^2}\alpha + {{\left( {\frac{{{\upsilon ^2}}}{R}} \right)}^2}}\)
Ответ: \(65 м/с^2.\)
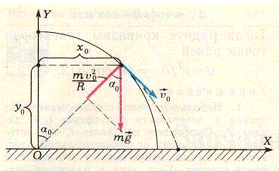
Объект малых габаритных размеров расположен на полусферическом теле. В какой-то момент времени рассматриваемый предмет начинает движение, начиная скольжение по поверхности с нулевым трением. Требуется вычислить координаты точки, в которой тело достигнет горизонтальной плоскости.
Источник: easyfizika.ru
Решение
В течение определенного временного промежутка после того, как началось скольжение предмета, он соскользнет со сферической поверхности. Когда этот момент настанет, можно будет наблюдать движение, аналогичное перемещению подброшенного объекта под углом к горизонтальной линии. Получив пару типичных примеров криволинейного движения, можно значительно упростить расчеты.
Сначала целесообразно изобразить координатную плоскость, как показано на схеме. Далее потребуется вычислить, чему равны начальные координаты точки, в которых находился предмет до того, как соскользнул со сферической поверхности, то есть \(x_0 и y_0\). Другой важной характеристикой служит модуль и направление скорости \(\overrightarrow {{\upsilon _0}}\) в момент отрыва.
Заметим, что в данной ситуации передвижение предмета по сферической траектории реализовано по причине эффекта со стороны пары сил. К таковым можно отнести, применительно к рассматриваемой задаче, силу тяжести \(m\overrightarrow g\) и силу нормальной реакции \(\overrightarrow N\). Когда объект соскользнул с поверхности, сила реакции принимает нулевое значение. По этой причине нормальное ускорение составляет:
\({a_н} = \frac{{{\upsilon ^2}}}{R}\)
В процессе предмету ускорение придает лишь воздействующая на него проекция силы тяжести:
\(\frac{{m\upsilon _0^2}}{R} = mg\cos {\alpha _0}.\)
Решая это уравнение совместно с уравнением, выражающим закон сохранения энергии:
\(\frac{{m\upsilon _0^2}}{2} = mgR\left( {1 – \cos {\alpha _0}} \right),\)
найдем
\(\cos {\alpha _0} = \frac{2}{3},\,\,{\upsilon _0} = \sqrt {\frac{{2gR}}{3}} .\)
Координаты точки отрыва равны, соответственно,
\({y_0} = R\cos {\alpha _0} = \frac{{2R}}{3},\)
\({x_0} = \sqrt {{R^2} – y_0^2} = R\sqrt {1 – {{\cos }^2}{\alpha _0}} = \frac{{\sqrt 5 R}}{3}.\)
Теперь запишем уравнения движения тела после отрыва от полусферы:
\(x = {x_0} + {\upsilon _0}\cos {\alpha _0} \cdot t,\)
\(y = {y_0} – {\upsilon _0}\sin {\alpha _0} \cdot t – \frac{{g{t^2}}}{2}.\)
Заметим, что при соприкосновении с горизонталью ордината принимает нулевое значение. Таким образом, у = 0. Абсциссу x можно вычислить по соотношению, описывающему перемещение предмета. При этом следует воспользоваться методом подстановки исходных условий, которые равны:
\((x_0, \upsilon_0 и \cos {\alpha _0})\)
Кроме того, следует учитывать временной промежуток до соприкосновения, исходя из нулевого значения для у. Тогда получим, что:
\(x \approx 1,12R.\)
Ответ: \(x \approx 1\),12R; y=0.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так