Период колебаний
Что такое колебательный процесс
Колебания — это движения или процессы, которые повторяются с определенным интервалом времени.
Систему, совершающую колебания, называют колебательной системой или осциллятором.
Исходя из физической природы, колебательные процессы бывают механического, электромагнитного и других видов.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Свободные или собственные колебания — колебания, которые наблюдают в системе, предоставленной себе после выведения из равновесного состояния.
Вынужденными колебаниями называют колебания, происходящие под действием внешней силы, изменяющейся периодически.
При механических колебаниях, которые относят к категории вынужденных:
\(F=F_{0}\cos \cot\)
Гармоническими колебаниями называют колебания, определяемые физической величиной, которая изменяется, согласно закону синуса или косинуса.
Разные периодические процессы, повторяющиеся в течение равных временных интервалов, могут быть записаны в виде суммы или суперпозиции гармонических колебаний.
Определение периода колебаний, формула
Колебательный процесс можно представить в виде уравнения. Тогда гармоническое колебание значения х будет представлено следующей формулой:
\(x(t)=A\times \cos \left(\omega _{0}t+\phi _{0} \right)\)
Где \(x(t)\) является отклонением колеблющейся физической величины от равновесного значения;
А представляет собой амплитуду гармонических колебаний;
\(\omega _{0}\) равно циклической или круговой частоте колебаний;
\(\phi _{0}\) является начальной фазой колебаний, характерной для момента времени t=0, что можно определить с помощью выбора начала отсчета времени;
\(cp(t)=(co_{0}t+cp_{0})\) описывает фазу колебаний в момент времени t, определяется в радианах, соответствует значению колеблющейся величины в данное время.
В случае, когда имеется какая-либо материальная точка с массой m, характеристика х будет соответствовать смещению тела из равновесного положения. Следует заметить, что амплитуда и частота гармонических колебаний обладают постоянными значениями. Исходя из того, что cos меняет значение в интервале от +1 до -1, параметр х будет изменяться от +А до –А. Так как:
\(\cos \left(\alpha +2\pi \right)=\cos \alpha,\)
то х остается без изменений при фазе колебаний, получающей приращение в $$2\pi$$
Период колебаний Т представляет собой минимальный временной интервал, в течение которого колебательная система возвращается в то состояние, в котором она находилась в начальный момент времени, определенный произвольно.
В этом случае фаза будет увеличена на \(2\pi:\)
\(\omega _{0}(t+T)+\phi _{0}=\left(\omega _{0}t+\phi _{0} \right)+2\pi\)
Из данного равенства можно вычислить период колебаний:
\(T=\frac{2\pi }{\omega _{0}}\)
Частота колебаний v является величиной, которая обратна периоду колебаний. Это количество полных колебаний, выполняемых за единицу времени:
\(v=\frac{\omega _{0}}{2\pi}\)
На графике изображены гармонические колебания, где а — зависимость смещения х от времени /, б — зависимость скорости vx от времени С, в — зависимость ускорения ах от времени t.
Единицей частоты в СИ является герц (Гц). Это частота периодического периода, в котором в течение 1 секунды выполняется одно полное колебание.
Можно представить, что материальная точка совершает прямолинейные гармонические колебания, относительно оси Х около равновесного положения, которое является началом отсчета координат. Так как движения частицы колебательные, ей присуще скорость и ускорение. Характеристики данного процесса будут записаны таким образом:
Смещение \(x=A\times \cos \left(\omega _{0}t+\phi _{0} \right)\)
Скорость \(v_{x}=\dot{x}=-A\omega _{0}\times \sin \left(\omega _{0} t+\phi_{0} \right)=A\omega _{0}\times \cos \left(\omega _{0} t+\phi_{0} +\frac{\pi }{2}\right)\)
Ускорение
\(a_{x}=\dot{v_{x}}=\ddot{x}=-A\omega _{0}\times \cos \left(\omega _{0} t+\phi_{0} \right)=A\omega _{0}^{2}\times \cos \left(\omega _{0} t+\phi_{0} +\pi \right)\)
Как найти период для физического маятника
В случае, когда углы отклонения \(\varphi\) небольшие, физический маятник будет совершать гармонические колебания. Можно считать его вес, приложенным к центру тяжести в точке С. Сила возврата маятника в равновесное положение является составляющей силы тяжести — сила F:
\(F=mg\times \sin \varphi\)
Отрицательное значение правой части уравнения означает, что сила F ориентирована по направлению уменьшения угла \(\alpha\)
Учитывая малый угол \(\varphi\) уравнение можно записать в следующем виде:
\(F=mg\times\varphi\)
С помощью основного уравнения динамики, описывающее вращательное движение, можно вывести закон движения физического маятника:
\(J=ml^{2}\)
При условии невозможности определения момента силы в явном виде, дифференциальное уравнение колебаний физического маятника будет записано в такой форме:
\(\frac{d^{2}\varphi }{dt^{2}}+\frac{mgl}{J}\varphi =0\)
В результате сравнения полученного выражения и уравнения гармонических колебаний, получим:
\(\alpha _{x}(t)+\omega ^{2}x(t)=0\)
Таким образом, получается, что формула циклической частоты пружинного маятника имеет следующий вид:
\(\omega =\sqrt{\frac{mgl}{J}}\)
В таком случае для расчета периода колебаний математического маятника будет использоваться формула:
\(T =\frac{2\pi }{\omega }=2\pi \sqrt{\frac{J}{mgl}}\)
Исходя из расчетов, можно сделать следующие выводы:
- Период пружинного маятника \(T =2\pi \sqrt{\frac{m}{k}}\)
- Период математического маятника \(T =2\pi \sqrt{\frac{L}{g}}\)
- Период крутильного маятника \(T =2\pi \sqrt{\frac{I}{K}}\)
В приведенных формулах:
- T — период физического маятника;
- J — момент силы маятника относительно оси вращения;
- l — расстояние от оси вращения до центра масс;
- m — масса маятника;
- g=9.8 — ускорение свободного падения.
Примеры решений
Шариком, привязанным к нити, совершено 60 колебаний в течение 2 минут. Необходимо определить, каковы период и частота колебаний шарика.
Решение
\(T =\frac{t}{N}=\frac{120}{60}=2\)
\(V=\frac{1}{T}=\frac{1}{2}=0.5\)
Ответ: период колебаний маятника равен 2 секундам, а частота составляет 0,5 Гц.
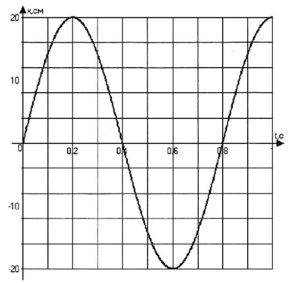
Согласно изображенного графика зависимости координаты от времени, необходимо рассчитать характеристики колебательного движения тела.
Решение
А = 20
Т = 0,8
\(V=\frac{1}{T}=\frac{1}{0,8}=1,25\)
\(x(t)=A\sin 2\pi Vt=0.2\sin 2\pi \times 1.25t=0.2\sin 2.5\pi t\)
Ответ: амплитуда колебаний маятника составляет 0,2 метра, период колебаний соответствует 0,8 с, частота колебаний равна 1,25 Гц, уравнение координаты будет записано в следующем виде: \(x(t)=0.2\sin 2.5\pi t\)
Необходимо определить, какой длиной обладает математический маятник, который совершает гармонические колебания при частоте 0,5 Гц на поверхности Луны. Ускорение свободного падения в данном случае составляет 1,6 м/с2.
Решение
Период колебаний математического маятника рассчитывается по формуле:
\(T =2\pi \sqrt{\frac{L}{g}}\)
Согласно определению:
\(V=\frac{1}{T}\)
Тогда:
\(T=\frac{1}{V}\)
Получим равенство:
\(\frac{1}{V}=2\pi \sqrt{\frac{l}{g}}\)
Для того чтобы выразить длину маятника, необходимо возвести обе части равенства в квадрат:
\(\frac{1}{V^{2}}=4\pi ^{2}\times \frac{l}{g}\Rightarrow l=\frac{g}{4\pi ^{2}V^{2}}\)
\(l=\frac{1.5}{4*3.14 ^{2}*0.5^{2}}\approx 0.16\)
Ответ: длина математического маятника примерно составляет 0,16 метра.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так