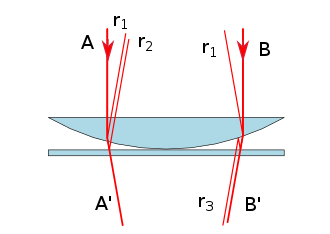
Интерференционные полосы равной толщины и равного наклона

Что такое интерференция

Это явление играет важную роль в различных областях науки и техники. В оптике, интерференция используется для создания интерференционных рисунков, которые помогают исследовать свойства света. Эти рисунки могут быть использованы для определения длины волны, направления распространения света, а также для измерения расстояний до объектов.

Интерференция также применяется в различных приборах, таких как интерферометры, которые используются в научных исследованиях для измерения различных физических величин. Они могут быть использованы для измерения расстояний, скорости, ускорения и других параметров.

История изучения интерференции

Первые исследования интерференции были проведены Томасом Юнгом в 1801 году. Он провел эксперимент, который включал в себя использование двух щелей, через которые проходили световые лучи. Юнг обнаружил, что на экране, расположенном за щелями, возникают светлые и темные полосы, что свидетельствует о наличии интерференции. Это наблюдение подтвердило волновую теорию света и легло в основу дальнейших исследований этого явления.

Так выглядел Томас Юнг: 

Источник: ru.wikipedia.org

Позднее, в 19 веке, физик Френель провел более детальные исследования интерференции и доказал, что она может наблюдаться не только на световых волнах, но и на звуковых и других видах волн. Он показал, что интерференция происходит в тех случаях, когда несколько волн сливаются вместе и взаимодействуют друг с другом.

В последующие годы исследования интерференции продолжались, были разработаны более точные методы ее измерения, что привело к созданию новых научных теорий и открытий. Сегодня интерференция является ключевым явлением в разных областях науки и техники, таких как радиофизика, оптика, акустика, и другие.

Так выглядел Огюстен Жан Френель: 

Источник: ru.wikipedia.org

Современные исследования интерференции позволили раскрыть новые аспекты этого явления, например, интерференцию между волнами различных частот. Это нашло свое применение в технологиях радиосвязи и радиолокации. Кроме того, интерференция широко используется в оптических приборах, например, в интерферометрах, которые позволяют измерять длину волн света с высокой точностью.

Полосы равной толщины

При прохождении света через пластину происходит его разделение на две лучевые волны, которые затем интерферируют друг с другом. В результате интерференции образуются светлые и темные полосы. Если толщина пластины равна длине волны света, то на экране образуется ряд равных по ширине светлых и темных полос.

Полосы равной толщины в интерференции широко используются в оптике для измерения толщины пластин и других прозрачных материалов, а также для исследования их оптических свойств. Оптические методы, основанные на явлении полос равной толщины, позволяют измерять толщину пластин с высокой точностью и чувствительностью. Этот метод применяется в различных областях науки и техники, таких как микроэлектроника, медицина, материаловедение и т.д.

Кроме того, явление полос равной толщины в интерференции используется для исследования оптических материалов, таких как стекло, кристаллы и полимеры. Изучение интерференционных полос позволяет определить коэффициент преломления материала, его показатель дисперсии и другие оптические параметры. Этот метод широко применяется в научных исследованиях и в производстве оптических приборов.

Таким образом, явление полос равной толщины в интерференции имеет широкое применение в оптике и науке в целом, и является важным инструментом для измерения и исследования свойств оптических материалов.

Полосы равного наклона

Полосы равного наклона возникают при интерференции света и представляют собой яркие и темные прямые полосы, которые наблюдаются на плоской поверхности при наличии определенных условий. Для того, чтобы возникли полосы равного наклона, необходимо, чтобы на поверхность пластины падал параллельный пучок света. Кроме того, пластина должна быть оптически однородной и иметь постоянную толщину.

Однако, если пластинка наклонена на некоторый угол, то разность хода между лучами изменяется, что приводит к образованию темных полос. Угол наклона пластинки, при котором возникают полосы равного наклона, зависит от длины волны света и толщины пластинки. Поэтому, изменяя угол наклона пластины, можно получить различную интерференционную картину.

Полосы равного наклона нашли широкое применение в научных и технических областях, благодаря своей способности измерять толщину пластин и определить показатель преломления материалов. Кроме того, они используются в микроскопии, лазерных технологиях и других областях, связанных с оптикой и светом.

Таким образом, полосы равного наклона представляют собой важное явление в интерференции света, которое имеет широкое практическое применение в различных областях науки и техники.

Кольца Ньютона

Кольца Ньютона были названы в честь знаменитого ученого Исаака Ньютона, который первым изучал интерференцию света в 17 веке.

Чтобы наблюдать кольца Ньютона, необходимо использовать микроскоп и специальную пластину, состоящую из двух стеклянных пластин. Одна из этих пластин выпуклая, а другая — плоская.

Когда световые лучи проходят через такую пластину, они отражаются от плоской поверхности и проходят через выпуклую поверхность, создавая интерференционные кольца. Эти кольца обладают различной яркостью и цветом, что позволяет использовать их для измерения толщины воздушного зазора между стеклом и пластиной.

Так образуются кольца Ньютона: 

Источник: ru.wikipedia.org

Кольца Ньютона нашли широкое применение в различных областях науки и техники. Они используются для измерения толщины тонких пленок, прозрачных пластин, определения показателя преломления материалов, а также для измерения длины волн света. Это свойство находит применение в микроэлектронике, лазерных технологиях, оптике и других областях.

Кольца Ньютона являются важным инструментом для измерения малых расстояний и толщин, и их использование продолжает находить новые области применения в науке и технике. Они также могут быть использованы для изучения различных свойств материалов, таких как прочность, твердость и эластичность.

Примеры решения задач 

Решение: 

Получается, что в этой задаче волна, которая исходит от радиомаяка, будет интерферирована с волной, которая отражается от водной поверхности. Условие m-го максимума рассчитывается так: 

\(y_{m}=\frac{(2m-1)d\lambda}{4H}\)

Чтобы найти оптимальную высоту корабельной мачты, предположим, что m=1. Получается: \(y=\frac{d\lambda}{4H}=\frac{5500\times1,5}{4\times200}=10,3\)

Ответ: 10,3 м.

Решение: 

В монохроматическом свете, который отражается, радиусы светлых колец равняются

В отраженном монохроматическом свете радиусы светлых колец равны: \(r=\sqrt{\frac{(2m+1)R\lambda}{2}}\). Радиус кривизны линзы можно найти таким образом: \(R=\frac{4r^{2}}{(2m+1)\lambda}=\frac{4(1,4\times10^{-3})^{2}}{(2\times3+1)\times589\times10^{-9}}=1,9 м. \) 

Ответ: 1,9 м.