Определение силы натяжения нити

Сила натяжения нити — формулировка

Длина тела, к которому приложена сила, обычно многократно больше, чем его толщина. Примерами таких объектов являются веревка, канат, трос, леска, проволока. Сила натяжения визуально проявляется в следующих примерах:

• создание строительного отвеса;
• установка растяжек для фиксации радиоантенн;
• поведение арматуры внутри напряженного бетона;
• устройство корабельного такелажа.

Как определить силу, формулы

Натяжение проявляется по-разному. Поэтому сила натяжения может рассчитываться определенным образом, в зависимости от окружающих условий.

С неподвижно закрепленным верхним концом

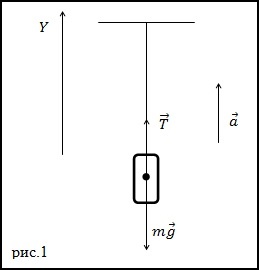
Простейшим примером проявления силы натяжения является нить с закрепленным на ней грузом. Верхний конец такого подвеса фиксируется неподвижно. В этом случае сила натяжения будет соответствовать силе тяжести, которая действует на тело. Формула для расчета:

\(F=F_{тяж}=m*g\)

где m – это масса тела, а g представляет собой ускорение свободного падения.

Если нить под углом

В случае, когда груз расположен под определенным углом, характер силы натяжения несколько изменяется. Примером такой системы выступает маятник. 

\(F_n=m*g*cos(a)\)

где а равен углу отклонения.

Формула с учетом ускорения и массы

В ситуации, при которой на груз оказывается сила натяжения, приводящая его в движение вверх, следует использовать такую формулу для ее расчета:

\(F=F_{тяж}+m*a\)

Сила натяжения во вращающейся системе

Описание

Такое явление можно наблюдать, когда система из нити и тела вращается во время раскручивания подвеса вокруг своей оси с закрепленным на одном его конце объектом: центрифуга, маятник, качели. Сила натяжения, возникающая внутри подвеса, характеризуется центробежной силой и в условиях вращения в вертикальной плоскости циклически претерпевает изменения. То есть можно наблюдать зависимость силы от угла отклонения от вертикали:

• приближение к земле приводит к увеличению силы;
• во время удаления от земли сила слабеет.

Формула расчета

Рассчитать силу натяжения в условиях вращающейся системы можно так:

\(F=\frac{m\times \nu ^{2}}{r}\)

Обозначение, единица измерения

Существуют определенные стандарты для написания формулы силы натяжения. Как и другие физические силы, натяжение обозначается F. В качестве единицы измерения используют Ньютон (H)

\(H=\frac{kg\times m}{c^{2}}\)

Примеры решения задач

Задание 1

На невесомую нерастяжимую нить действует сила натяжения Т=4400Н. Необходимо определить максимальное ускорение подъема груза, масса которого равна m=400 кг, подвешенного на этой нити. При этом нить должна сохранить целостность.

Решение

Представив все силы, оказывающие действие на тело, необходимо составить формулу второго закона Ньютона. Тело является материальной точкой, а силы приложены к центру его массы.

\(\bar{T}+m\bar{g}=m\bar{a}\)

\(\bar{T}\) является силой натяжения нити.

Проекция уравнения будет иметь следующий вид:

\(T – mg = ma\)

Данное выражение позволяет рассчитать ускорение:

\(a=\frac{T-mg}{m}\)

Так как все величины, изложенные в задании, соответствуют единицам СИ, можно провести корректные вычисления

\(a=\frac{4400-4*9,8}{400}\)

Ответ: a = 1.2 \(м/с^2\)

Задание 2

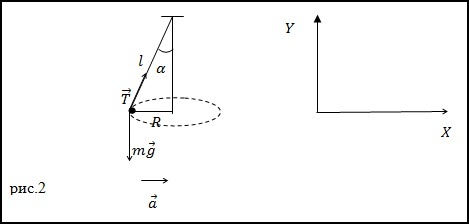
На иллюстрации изображен шар, который обладает массой m=0.1 кг. Будучи зафиксирован на нити, шарик совершает движение по окружности в горизонтальной плоскости. Длина подвеса составляет l=5 м, а радиус окружности – R=3 м. Требуется вычислить модуль силы натяжения нити.

Решение

Необходимо воспользоваться вторым законом Ньютона и записать его для сил, которые действуют на шар. Центростремительное ускорение при его вращении по окружности будет записано следующим образом:

\(\bar{T}+m\bar{g}=m\bar{a}\)

Проекции данной формулы по осям определяются следующим образом:

X:  \(T sin α = ma = mω2R\)

Y:  \(-mg + T cos α = 0\)

Таким образом, из уравнения Y получаем расчет модуля силы натяжения нити:

\(T=\frac{mg}{\cos \alpha }\)

Анализ рисунка позволяет вывести следующее уравнение:

\(\sin \alpha = \frac{R}{l}\rightarrow \cos \alpha = \sqrt{1-\left(\frac{R}{l} \right)^{2}}\)

Если cos α заменить уравнением для расчета модуля силы натяжения нити, то получим следующую формулу:

\(T=\frac{mg}{\sqrt{1-\left(\frac{R}{l} \right)^{2}}}= \frac{mgl}{\sqrt{l^{2}-R^{2}}}\)

Значения основных величин, выраженные в СИ, можно подставить в конечную формулу для расчета силы натяжения нити:

\(T=\frac{0,1*9,8*5}{\sqrt{5^{2}-3^{2}}}=1,225\left(H \right)\)

Ответ: Т=1,225 H