Что называется степенью статической неопределимости

Степень статической неопределимости — что это такое

Стержневая система, исходя из положений строительной механики и сопромата, представляет собой конструкцию, которая воспринимает нагрузки и состоит из стержней. Они могут быть шарнирно или жестко сопряжены между собой. Данные конструкционные элементы функционируют либо на растяжение, либо на сжатие. В этом случае конструкция является фермой.

Ферма включает некоторое количество прямых стержней, шарнирно соединенных друг с другом. Фермы характеризуются приложением внешних усилий в узлах, то есть местах примыкания двух и более стержней. В том случае, когда некий стержень в большей степени работает на изгиб, то систему называют рамой.

При расположении всех компонентов шарнирно-стержневой системы и приложенных к ней нагрузок в рамках одной плоскости, систему называют плоской. При расположении всех элементов системы в одной плоскости и перпендикулярно приложенных внешних усилиях, включая реакции опор, систему считают плоско-пространственной.

Стержневые системы, которые нельзя отнести ни к одной из перечисленных категорий, являются пространственными.

Любые шарнирно-стержневые системы подразделяется на следующие статистические группы:

• статически определимые;
• статически неопределимые.

Если усилия во всех элементах системы можно определить с помощью метода сечений с применением лишь уравнений равновесия, то система является статически определимой. При отсутствии возможности выполнить подобный расчет систему называют статически неопределимой.

Общие понятия, особенности

Статически неопределимые системы представляют собой стержневые системы, в которых реакции опор невозможно определить, используя лишь уравнения равновесия. Количество связей, наложенных на статически неопределимую систему, увеличивается по сравнению с числом связей, обеспечивающих геометрическую стабильность конструкции. Такими связями могут являться:

• опорные связи;
• стержни конструкции.

Раскрыть смысл понятия статически неопределимой системы целесообразно путем изучения балок и простых рам. Связи в этих конструкциях обеспечивают геометрическую неизменяемость и представляют собой опорные закрепления или опорные связи. Для того чтобы обеспечить геометрическую стабильность балки или рамы в плоскости, необходимо наличие трех связей, каждая из которых препятствует какому-то перемещению.

Шарнирно-подвижная опора ограничивает перемещение по направлению, перпендикулярному плоскости опирания, и представляет собой одну связь. Благодаря шарнирно-неподвижной опоре становятся невозможными линейные перемещения по двум направлениям, которые взаимно перпендикулярны друг другу, то есть вертикальному и горизонтальному.

Данная опора характеризуется двумя связями, наложенными на конструкцию. При жестком защемлении конец стержня становится недоступным для любых перемещений:

• вертикального;
• горизонтального;
• угла поворота.

В связи с этим жесткое защемление является тремя связями, которые обеспечивают геометрическую стабильность балки или замкнутой рамы. Любая дополнительная связь, кроме трех имеющихся, в случае плоских систем делает конструкцию статически неопределимой.

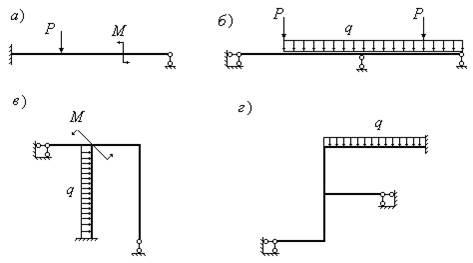
На рисунке изображены примеры статически неопределимых балок и рам:

С целью раскрытия статической неопределимости рассматриваемых систем составляют дополнительные уравнения совместимости деформаций. Рассчитать отдельные статически неопределимые стержни, которые работают на растяжение-сжатие, кручение, изгиб, можно с помощью группы соотношений, в которые включены уравнения равновесия, геометрические и физические уравнения. Количество таких уравнений зависит от числа статической неопределимости стержневой системы.

Определение общих параметров заданной системы

Способы расчета статически неопределимых систем:

1. Метод сил, в котором ключевыми искомыми параметрами являются усилия в лишних связях. С помощью данных характеристик, используя метод сечений, можно определить усилия, возникающие в поперечных сечениях элементов рассматриваемой системы.
2. Метод перемещений – подразумевает расчет с применением перемещений узловых точек, спровоцированных деформационным изменением системы, как основных искомых величин. Зная эти перемещения, можно определить все внутренние усилия, которые возникают в поперечных сечениях элементов рассматриваемой системы.
3. Метод конечных элементов – заключается в разбивке системы на простые конечные элементы и определении с помощью матрицы жесткости элемента и системы в общем, каким образом связаны перемещения узлов элемента и системы и усилия в них.
4. Смешанный метод, предполагающий определение части неизвестных в виде усилий, а другой части – в виде перемещений.
5. Комбинированный метод – позволяет рассчитать симметричные системы на несимметричные нагрузки.

Кроме того, методы расчета статически неопределимых систем классифицируют:

• исходя из степени точности;
• в зависимости от области работы материала сооружений;
• согласно особенностям расчетных операций.

Точные методы расчета основаны на типичных ключевых допущениях, которые приняты при рассмотрении достаточно жестких сооружений:

• закон Гука;
• деформационная схема расчета;
• правило сложения действия сил.

В приближенных методах расчета, помимо классических, применяют дополнительные допущения, что объясняет существенное отклонение от результатов, полученных точными методами расчета.

Исходя из области работы материала, сооружения рассчитывают:

• в упругой стадии;
• за пределом упругости.

Ориентируясь на особенности расчетных операций, методы расчета классифицируют на следующие категории:

• вычислительные;
• экспериментальные.

Степень статической неопределимости является разностью между числом неизвестных усилий, к примеру, реакций опор или внутренних силовых факторов, и количеством независимых уравнений равновесия, которые допустимо записать при рассматриваемой системе. Связи, наложенные на шарнирно-стержневую систему, классифицируют на следующие типы:

• внешние связи, в виде ограничений, накладываемых на абсолютные перемещения узлов или сечений системы;
• внутренние связи, которые ограничены лишь относительными перемещениями компонентов системы.

Таким образом, причинами статической неопределимости могут являться внутренние или внешние связи. В том случае, когда имеют место внешние связи, для описания положения объекта в какой-то плоскости XY используют три независимых параметра:

• две координаты;
• угол поворота заданной плоскости.

Исходя из этого, нужное для обеспечения равновесного состояния системы количество связей равно трем, согласно числу уравнений равновесия:

Σx = 0, Σy = 0 и Σm = 0

В том случае, когда какая-то плоская система обладает D частями, рассматриваемыми в виде жестких тел, число параметров, нужных для определения положения данной системы, составляет 3D. Каждый из шарниров, соединяющих пару частей системы, допускает лишь взаимный поворот этих двух частей. В результате с помощью шарнира исключается вероятность взаимного смещения частей системы.

Таким образом, ввод шарнира снижает число вероятных перемещений системы на пару единиц. Кроме того, каждый опорный стержень устраняет риски смещения системы в соответствующем направлении. Степень статической неопределимости, определяемая внешними связями, рассчитывается по формуле:

W = 3D – 2Ш – С

где D – является числом дисков (частей) рассматриваемой системы, каждый из которых может анализироваться в виде абсолютно жесткого тела;

Ш – представляет собой количество шарниров в системе, которые соединяют диски;

С – число опорных стержней.

Статически определимой системой можно назвать такую, при которой:

W = 0.

Предположим, что имеются две рамы с тремя и пятью внешними связями. В первом случае шарнирно-стержневая конструкция обладает необходимым для статической определимости числом шарниров и стержней. Во втором примере система отличается наличием двух дополнительных внешних связей.

При этом в обеих ситуациях рамы являются статически неопределимыми, так как обладают конфигурацией, не позволяющей определить усилия во всех стержнях с помощью уравнения статики. В связи с этим, окончательно ответить на вопрос о статической определимости можно путем анализа совместно наложенных и внутренних связей системы.

Способы рассмотрения статически неопределимых систем имеют в своей основе определение перемещений их узлов. Выше был описан метод начальных параметров. При всех преимуществах данного способа, он характеризуется одним значительным недостатком, который заключается в очень громоздких вычислительных формулах при большом числе расчетных участков.

Данное обстоятельство негативно отражается на расчетах криволинейных стержневых систем. Наиболее универсальной методикой расчета считают метод Мора. С его помощью определить линейное или угловое перемещение можно путем анализа двух состояний системы:

• действительное;
• вспомогательное.

Вспомогательное состояние достигается при устранении заданных нагрузок и приложении единичного усилия (F = 1) в том месте, где требуется рассчитать перемещение. В местах, где необходимо рассмотреть линейное перемещение, к примеру, прогиб балки или элемента рамы, прикладывают сосредоточенную силу (F = 1). Если необходимо найти угол поворота узла, то целесообразно приложить сосредоточенную пару сил (M = 0).

Свойства статически неопределимых систем

Статически неопределимые системы характеризуются рядом особенностей. Основными их свойствами являются:

1. Обладание большей жесткостью, чем аналогичная статически определимая система, при наличии добавочных лишних связей.
2. Возникновение меньших внутренних усилий, благодаря чему они являются более экономичными в сравнении со статически определимыми системами в условиях равных внешних нагрузок.
3. В результате разрушения лишних связей в нагруженном состоянии вся система сохраняет целостность. Это объясняется возникновением новой геометрически стабильной системы при устранении лишних связей. С другой стороны, отсутствие связи в статически определимой системе сопровождается изменениями в этой системе.
4. Рассчитать статически неопределимые системы можно путем предварительного определения геометрических характеристик поперечных сечений элементов, их формы и размеров, так как изменение данных параметров влечет за собой изменение усилий в связях и новое распределение усилий во всех компонентах системы.
5. В процессе расчета статически неопределимых систем следует заранее определить материал конструкции, так как потребуются данные о его модулях упругости.
6. Появление дополнительных усилий в статически неопределимых системах может быть вызвано температурным воздействием, осадкой опор, неточностями при их изготовлении и монтаже.