Определение вектора напряженности электрического поля: что характеризует

Вектор напряженности электрического поля — что из себя представляет

В 1831 году Майкл Фарадей установил закон электромагнитной индукции, обнаружив, что меняющееся во времени магнитное поле порождает электрическое. Выяснилось, что первично электромагнитное поле, а электрические и магнитные поля — различные его проявления. Позже Максвеллу удалось найти систему уравнений, которым подчиняется электромагнитное поле.

Основная характеристика

Пространство около электрического заряда отличается от пустоты, даже если заряд находится в вакууме. В этом случае говорят о присутствии поля, способного действовать на любой другой заряд. Взаимозависимость силы воздействия точечных зарядов и их величины описывает закон Кулона.

Поэтому для описания поля обычно прибегают к понятию силы, с которой оно действует на положительный заряд, равный единице: такую характеристику называют напряженностью и обозначают \(\overrightarrow{Е}\). Она равна отношению силы к величине заряда, на который та воздействует.

Таким образом, вектор напряженности электрического поля является его силовой характеристикой. Единица ее измерения — вольт на метр или в ньютон на кулон. 

Определение параметров электрического поля

Зная величину внесенного в поле заряда q, можно рассчитать силу в каждом конкретном случае:

\(\overrightarrow{F} = q \times\overrightarrow{Е}\)

Согласно закону Кулона, напряженность поля вокруг неподвижного точечного заряда q описывается выражением:

\(\overrightarrow{Е} = k \times \frac{q}{r^{2}} \times \frac{\overrightarrow{r}}{r}\)

\(k\) равен \(\frac{1}{4\pi \epsilon_{0}}\)

\(\epsilon_{0}\) — электрическая постоянная, равная \(8,85\times 10^{-12}\) Ф/м.

Для вычисления напряженности всего поля нужно сложить напряженности полей отдельных зарядов, т. е. воспользоваться принципом суперпозиции:

\(\overrightarrow{Е} = \overrightarrow{Е_{1}} + \overrightarrow{Е_{2}}\)

Если во всех точках поля напряженность одинакова, оно считается однородным. Если она различается — неоднородным.

Какое направление имеет вектор, как определить

Напряженность по направлению совпадает с силой, с которой поле воздействует на единичный заряд. Если оно создано положительным зарядом, происходит отталкивание: вектор направлен от заряда во внешнее пространство. Если отрицательным зарядом, вектор будет направлен к нему.

Также напряженность тесно связана с напряжением — вектор напряженности всегда направлен в сторону уменьшения потенциала, а сама она равна его градиенту, т. е. скорости его изменения. К эквипотенциальной поверхности вектор напряженности перпендикулярен в каждой точке.

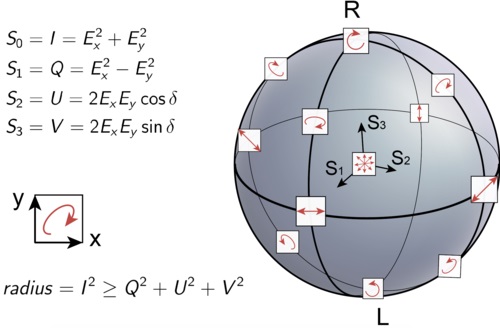
Направленное колебание векторов напряженности в электромагнитной волне называется поляризацией. Она бывает круговой, эллиптической и линейной — в зависимости от формы кривой, вычерчиваемой концом вектора амплитуды. Круговая или эллиптическая поляризация может быть правой или левой, что определяется направлением вращения вектора.

Чтобы описать поляризацию волны, компоненты вектора напряженности выражают с помощью параметров Стокса, интерпретируя их, как координаты точек, расположенных на сфере, называемой сферой Пуанкаре.

Поток вектора напряженности, применение теоремы Гаусса

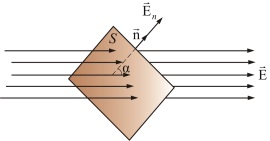
Суть теоремы, сформулированной Карлом Фридрихом Гауссом, сводится к следующему: если представить, что заряды окружены замкнутой поверхностью S, тогда поток вектора напряженности электрического поля через элементарную площадку \(\triangle S\) можно записать как:

\(\triangle Ф = Е\cos\alpha\triangle S\)

\(\alpha\) здесь — угол между нормалью к площадке и \(\overrightarrow{Е}\).

Тогда поток через площадку \(S\) описывается формулой:

\(Ф = Е_{n}S\)

\(Е_{n}\) здесь — модуль нормальной составляющей поля \(\overrightarrow{Е}\), произведение вектора \(\overrightarrow{Е}\) на нормаль \(\overrightarrow{n}\) к данной площадке.

Поскольку взаимодействия между зарядами не имеют значения, расчеты значительно упрощаются. С помощью теоремы Гаусса можно рассчитать поле любого числа зарядов, но это реализуемо только в случае их симметричного расположения, когда можно выбрать поверхность, через которую получится рассчитать поток напряженности.