Закона Био-Савара-Лапласа: формула и определение
Формулировка закона Био-Савара-Лапласа
Закон Био Савара Лапласа — эксперимент, проведенный французскими физиками Био и Саваром. В нем они определили индукцию магнитного поля в точке из-за малого элемента тока. Закон сформулировал Лаплас.
С помощью данного закона определяется напряжение магнитного поля H возле проводника с токос. Он дает соотношение между напряжением магнитного поля, генерируемого элементом тока его источника.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Величина магнитного поля в точке, создаваемого вокруг проводника небольшой длины из-за протекания через него тока прямо пропорциональна:
- длине проводника;
- величине тока;
- синусу угла между линиями, соединяющими точку от середины проводника до самого проводника;
- обратно пропорциональна расстоянию между точкой и серединой проводника.
С помощью уравнения Био Савара можно описать магнитное поле, которое создается токопроводящим проводником. Оно позволяет рассчитать напряжение на разных участках.
История открытия закона
Эрстед
К концу 18-го века ученые заметили много электрических явлений и магнитных явлений, но большинство полагало, что они были взаимосвязанными. Были некоторые причины полагать, что связь может быть. Давно было известно, что компас при ударе молнии может менять полярность. Эрстед ранее отмечал сходство между тепловым излучением и светом, хотя и не определил, что и то, и другое являются электромагнитными волнами. Похоже, он верил, что электричество и магнетизм — это силы, излучаемые всеми веществами, эти силы могут каким-то образом быть взаимосвязанными.
Во время лекции в 1820 году, настраивая свой аппарат, физик заметил, когда он включил электрический ток, подсоединив провод к обоим концам батареи, магнитная стрелка компаса, находящаяся поблизости, отклонилась от севера, куда она обычно указывала. Она сдвинулась лишь слегка, никто кроме ученого этого не заметил.
Эрстед был хорошо подготовлен к наблюдению такого эффекта, имея под рукой стрелку компаса и батарейку (или гальванический аппарат, как он это называл). Он не сразу нашел математическое объяснение, но обдумывал его в течение следующих трех месяцев, а затем продолжал экспериментировать, пока не убедился окончательно, что ток может создавать магнитное поле (которое он назвал «электрическим конфликтом»).
Био и Савар
На заседании 30 октября того же года Био и Савар прочитали в Академии наук доклад, целью которого является определение путем точных измерений физических законов, согласно которым металлические провода, соединенные с двумя полюсами вольтового аппарата, воздействуют на магнитные тела.
Они измерили скорость колебаний подвешенного магнита, расположенного на различных расстояниях от проводника, по которому проходит ток. Они смогли продемонстрировать движение магнитной силы под прямым углом к перпендикуляру, соединяющему рассматриваемый участок с проводником, а также ее интенсивность обратно пропорциональна расстоянию.
Формула
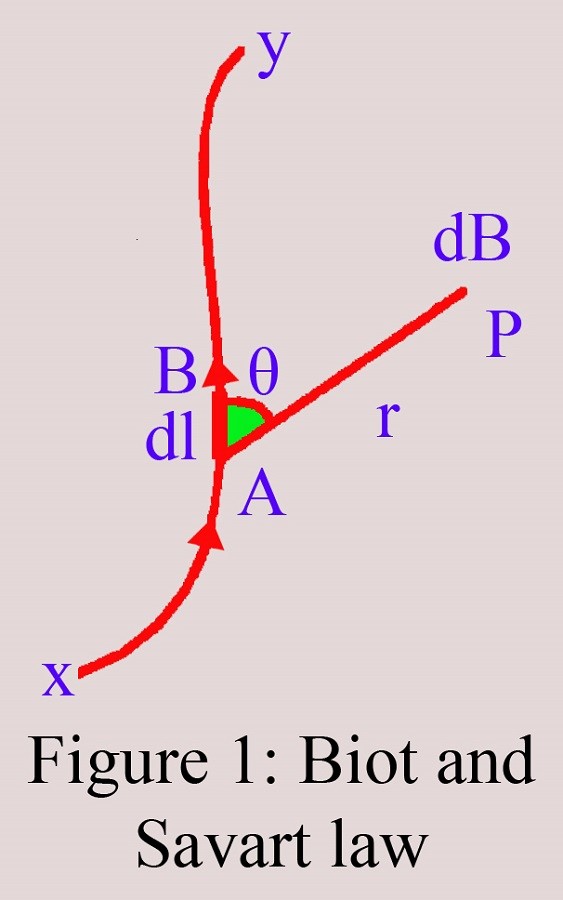
Проводник XY, по которому протекает ток I. Из-за этого оно окружено магнитным полем. Для того чтобы определить его наличие на участке P, рассмотрим как элемент AB длины dl, составляющий угол θ с линией, соединяющей r. Пусть отрезок P—dl равен r.
По закону Био Савара Лапласа, напряжение магнитного поля, создаваемого элементом на участке P:
- dB ∞ I,
- dB ∞ dl,
- dB ∞ sinθ,
- dB ∞ 1/r2.
Комбинируя эти факторы, мы получаем формулу:
\(dB\alpha\dfrac{I dl sin \theta}{r^2} dB = \dfrac{k I dl sin \theta}{r^2}\)
k — постоянная пропорциональности, а ее значение зависит от системы единиц, выбранной для измерения различных величин.
\(K = \dfrac{\mu_0}{4\pi}, или K = 1\)
Где μ0 — абсолютная магнитная проницаемость свободного пространства:
\(И \mu_0 = 4\pi 10^{-7}Wb A^{-1}m^{-1} = 4\pi 10^{-7}T A^{-1}m ( 1T = 1WB м-2)\)
\(dB = \dfrac{\mu_0}{4\pi}\dfrac{Idl sin\theta}{r^2}---(i)\)
Закон Био Савара Лапласа в векторной форме записывают так:
\(|d\vec{B}| = \dfrac{\mu_0}{4\pi}\dfrac{I|d\vec{l}\times\vec{r}|}{r^3}\)
или
\(d\vec{B} = \dfrac{\mu_0}{4\pi}\dfrac{I(d\vec{l}\times\vec{r})}{r^3}---(ii) \)
dB→
Индукция магнитного поля на участке P из-за тока равняется:
\(\vec(B) = \int\dfrac{\mu_0}{4\pi}\dfrac{I d\vec{l}\times\vec{r}}{r^3} B = \int\dfrac{\mu_0}{4\pi}\dfrac{Я dl sin\theta}{r^2}\)
Закон Био Савара в условиях плотности тока J гласит, что:
\(d\vec{B} = \dfrac{\mu_0}{4\pi}\dfrac{\vec{J}\times\vec{r}}{r^3}dV (J = \dfrac{1}{A} = \dfrac{I dl}{A dl} = \dfrac{I dl}{dV})\),
где J = плотность тока в любой точке текущего элемента, dV = объем элемента.
Закон Био Савара в условиях заряда (q) и его скорости (v) равен:
\(d\vec{B} = \dfrac{\mu_0}{4\pi}\dfrac{\vec{v}\times\vec{r}}{r^3}dV (I d\vec{l} = \dfrac{q}{dt}.d\vec{l} = q\dfrac{d\vec{l}}{dt} = q\vec{v} )\)
Закон Био Савара в условиях намагничивающей силы или намагничивания (H) магнитного поля s:
\(d\vec{H} = \dfrac{d\vec{B}}{\mu_0} = \dfrac{1}{4\pi}\dfrac{I d\vec{l}\times\vec{r}}{r^3} = \dfrac{1}{4\pi}\dfrac{I d\vec{l}\times\vec{r}}{r^2}\)
Особенности закона Био Савара Лапласа
- Закон Био Савара справедлив для симметричного распределения тока.
- Применим только к проводнику очень малой длины, пропускающему ток.
- Этот закон нелегко проверить экспериментально, поскольку невозможно получить токопроводящий проводник очень малой длины.
- Этот закон аналогичен закону Кулона в электростатике.
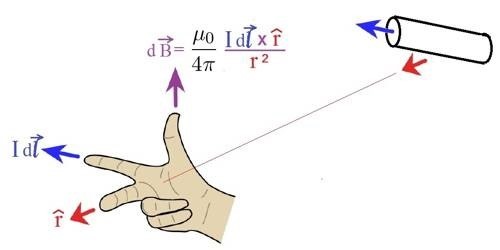
- Направление \(d\vec{B}\) перпендикулярно как I \(d\vec{l}\), так и \(\vec{r}\).
- Если \(\theta = 0^ 0\), т.е. точка P лежит на оси линейного проводника, несущего ток (или на проводе, несущем ток), то \(dB = \dfrac{\mu_0}{4\pi}\dfrac{I dl sin 0^0}{r^ 2} = 0\). Это означает, что ни в одной точке тонкого линейного токопроводящего проводника нет индукции магнитного поля.
- Если \(\theta = 90^ 0\), т.е. точка P лежит в перпендикулярном положении относительно текущего элемента, то \(dB = \dfrac{\mu_0}{4\pi}\dfrac{I dl}{r^ 2}\), что является максимумом.
- Если \(\theta = 90^0\) или \(180^0\), то dB = 0, т.е. минимум.
Применение
Для чего нужен закон Био Савара Лапласа. Закон важен по следующим причинам:
- Это фундаментальный закон магнитостатики.
- Этот закон может быть в равной степени применен к различным небольшим проводникам, по которым проходит электрический ток.
- Этот закон может быть применен для симметричного распределения тока.
Закон Био Савара Лапласа предоставляет ценный инструмент, который позволяет вычислять магнитные силовые поля, генерируемые электрическим током. Его открытие помогло добиться многих важных успехов в физике и технике: от определения поведения лампочек и двигателей до расчета магнитных сил, действующих на электроны в веществе.
Некоторые общие области применения закона Био Савара:
- для расчета магнитного поля, обусловленного постоянным током в прямом проводнике неопределенной длины;
- для определения магнитного поля вдоль оси круговой токопроводящей катушки;
- для расчета магнитных эффектов даже на атомном или молекулярном уровнях;
- в аэродинамике для расчета скорости, индуцируемой вихревыми линиями, т.к. магнитное поле является вращающейся силой (подобно земле, вращающейся вокруг солнца).
Примеры решения задач
Ток 5А проходит с юга на север по проводу, проложенному в направлении север-юг. Найдите магнитное поле, создаваемое отрезком проволоки длиной 1 см в точке на расстоянии 2 м к северо-востоку от отрезка проволоки.
Решение:
Приведенные данные: I = 5A,
r = 2 м,
Θ = 45°,
dl = 1 см = 1 × 10-2 м,
Найти: Магнитное поле (dB).
Формула: dB = μ0 / 4π [idlsinΘ / r2]
Расчет: По формуле dB = 10-7 × 6 × 10-2 × sin45° / 22 = 8,84 × 10-10 Т
Магнитное поле, создаваемое проводом в точке, составляет 8,84 × 10-10 Т.
Длинный прямой провод пропускает ток 35А. Каково магнитное поле B в точке в 20 см от провода?
Решение:
Приведенные данные: I = 35A,
a = 30 см = 0,3 м,
Найти: Поле магнитуды (B).
Формула: B = μ0 / 2π (I / a)
Расчет: По формуле B = 4π × 10-7 / 2π (35 / 0,3) = 2 × 10-7 (116.66)
B = 233,32 × 10-7 Т
Магнитное поле в точке 30 см составляет 233,32×10-7 Т.
Длинный прямой провод в горизонтальной плоскости пропускает ток 50А в направлении север-юг. Укажите величину и направление B в точке на расстоянии 3 м к востоку от провода.
Решение:
Приведенные данные: I = 50A,
a = 3 м,
Найти: Величину и направление B.
Формула: B = μ0I / 2na
Расчет: По формуле B = 4π × 10-7 × 50 / 2π × 3 = 2 × 10-7 × 50 / 3
B = 3,333 × 10-6 Т
Оно действует в направлении вертикально вверх, поэтому направление — вниз.
Примечание: Направление магнитного поля всегда находится в плоскости, перпендикулярной линии элемента и вектору положения.
Величина B составляет 4 × 10-6 T, а направление — вертикально вниз.
Два длинных прямых параллельных провода в вакууме находятся на расстоянии 4 м друг от друга и пропускают токи 6А и 8А в одном направлении. Найдите нейтральную точку, т.е. точку, в которой результирующая магнитная индукция равна нулю.
Решение:
Приведенные данные: I1 = 4A,
I2 = 8A,
r = 4 м.
Найти: нейтральную точку (точку, в которой результирующая магнитная индукция равна нулю).
Формула: (i) B1 = μ0 / 4π (2I1 / r1); (ii) B2 = μ0 / 4π (2I2 / r2).
Ток, протекающий по проводу, идет в одном и том же направлении. В результате в любом месте между двумя проводами две магнитные индукции B1 и B2 будут иметь противоположные направления. В результате точка должна располагаться между двумя проводами.
Чтобы результирующая магнитная индукция была равна нулю, должно быть B = B2. Пусть соответствующая точка (нейтральная точка) находится на расстоянии r1 от первого провода и r2 от второго провода.
Расчет:
B = μ0 / 4π ( 2I1 / r1) и B2 = μ0 / 4π ( 2I2 / r2)
B1 = B2
∴ I1 / r1 = I2 / r2
∴ r2 / r1 = I2 / I1
∴ r2 / r1 = 8A / 4A = 2
∴ r2 = 2r1
Но, r1 + r2 = r
∴ r1 + 2r1 = 4m
∴ r1 = 4/3 м и r2 = 8/3м
Нейтральная точка находится на расстоянии 4/3 м от провода, по которому проходит ток 4А.
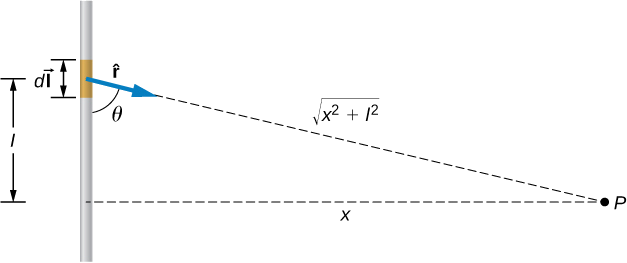
Короткий провод длиной 1 см пропускает ток 2 А в вертикальном направлении. Остальная часть провода экранирована, поэтому она не усиливает магнитное поле, создаваемое проводом. Рассчитайте магнитное поле в точке P, которая находится в 1 метре от провода в направлении x.
На этом рисунке показан провод I с коротким неэкранированным участком dI, по которому проходит ток. Точка P расположена на расстоянии x от провода. Вектор в точку P из dI образует угол Θ с проводом. Длина вектора равна квадратному корню из сумм квадратов x и I.
Решение: Мы можем определить магнитное поле в точке P, используя закон Био Савара. Поскольку текущий отрезок намного меньше расстояния x, исключаем интеграл из выражения. Интегрирование преобразуется обратно в суммирование, но только для малого dl, который мы теперь записываем как Δl. Угол θ
вычисляется с использованием тригонометрической функции. Используя приведенные числа, рассчитываем магнитное поле при P.
Расчет:
Угол между Δl→ и r^
вычисляется из тригонометрии, зная расстояния l и x от задачи: θ=tan−1(1m0.01m)=89,4o.
Магнитное поле в точке Р вычисляется по закону Био Савара: B=μ04πiδlsinθr2=(1×10−7T⋅m/A)(2A(0,01м)sin(89,4o)(1 м)2)=2,0×10−9T.
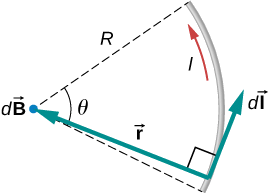
По проводу проходит ток I по дуге окружности радиусом R, проходящей под произвольным углом θ. Вычислите магнитное поле в центре этой дуги в точке P.
На данном рисунке показан кусок проволоки в форме дуги окружности радиусом R, изогнутой под произвольным углом тета. По проводу проходит ток dI. Точка P расположена в центре. Вектор r в точку P перпендикулярен вектору dI.
Решение:
Можно определить магнитное поле в точке P, используя закон Био-Савара. Радиальное направление и длина пути всегда находятся под прямым углом, поэтому перекрестное произведение превращается в умножение. Также расстояние по траектории dl связано с радиусом, умноженным на угол θ (в радианах).
Расчет:
Закон Био-Савара начинается со следующего уравнения: \(b⃗ =μ04π∫wireidl⃗ ×r^r2\)b.
Перекрестное произведение превращается в умножение, потому что путь dl и радиальное направление перпендикулярны. Можно подставить формулу длины дуги, dl=rdθ:
B=μ04π∫wireirdθr2.
Ток и радиус можно извлечь из интеграла, потому что они одинаковы независимо от того, где мы находимся на пути. При этом остается только интеграл по углу,
B=μ0I4nr∫wiredθ.
Угол на проводе изменяется от 0 до θ; следовательно, результатом является B=Μ0iθ4πr.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так