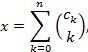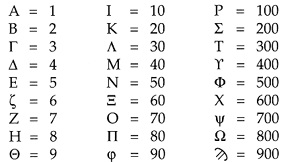Какие системы счисления называются непозиционными

Что таоке непозиционная система счисления в информатике

В информатике используют позиционный и непозиционный метод записи чисел. Позиционный способ предполагает представление числовых обозначений в определенной последовательности для сохранения величины числа.

Разновидности непозиционных систем счисления с примерами

Существует несколько видов непозиционной системы исчисления.

Биномиальная

В данном методе для записи чисел применяются биномиальные коэффициенты.

Число x в рассматриваемой системе представляет собой сумму биномиальных коэффициентов:

где, 0 <= c₁ < c₂ < ... < c_n.

Биномиальные числа бывают:

• линейные – в виде последовательности 0 и 1. Эта форма предполагает наличие двух чисел: количество столбцов в матрице и сумму числа столбцов и строк в матрице;
• матричные – в виде матрицы, элементами которой являются единицы и нули. При этом в одном столбце матрицы возможно наличие только одной 1. 

Пример преобразования матричной формы в линейную:

Каждой составляющей матрицы соответствует один биномиальный коэффициент. При сложении коэффициентов, соответствующих единицам в матрице, получится количественный эквивалент.  

Применение биномиальных чисел:

• действия с комбинаторных кодом – их получение, перебор и нумерация;
• шифрование информации и сжатие данных благодаря двоичному алфавиту данной системы счисления;
• представление решений генетических алгоритмов.

Греческая

В Греции рассматриваемый алфавитный способ записи чисел стал применяться в III веке до н.э. Буквы греческого алфавита соответствуют следующим числам:

С помощью ионийской системы можно записать лишь числа от 1 до 999.

Римская

Соответствие букв латиницы числовому значению:

• I — один;
• V — пять;
• X — десять;
• L — пятьдесят;
• C — сто;
• D — пятьсот;
• M — тысяча.

Для представления чисел десятичной системы счисления в виде римских букв работают следующие правила:

1. Стоящий слева от большего меньший символ вычитается из большего.
2. Стоящий справа от большего меньший символ прибавляется к большему.

Применение данной системы исчисления:

• обозначение знаменательных дат;
• разделов и глав книг;
• обозначение порядкового номера.

Древнеегипетская

Способ записи чисел, используемый в Древнем Египте, основывался на иероглифах. С помощью этих символов записывались основные числа 1, 10, 100 и т.д. Другие числовые значения получались с помощью сложения ключевых чисел.

Действие производилось в следующей последовательности:

1. Первым записывали число высшего порядка, после него – низшего.
2. Умножение и деление осуществлялось путем последовательного удвоения числовых значений.
3. Повторение каждой цифры допускалось до девяти раз.

Вавилонская

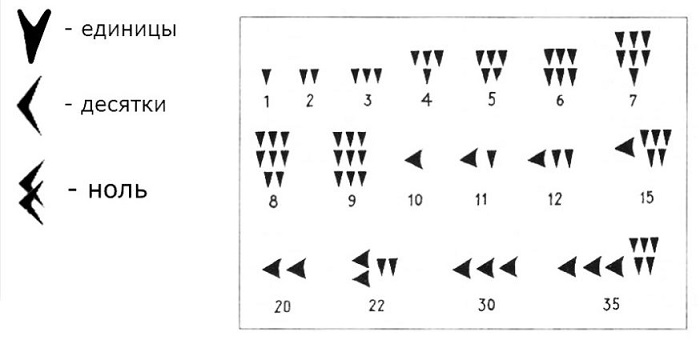
В данной системе счисления числа записываются справа налево в порядке убывания: сотни, десятки, единицы. Досчитав до 60, отмечают новый числовой ряд, запись чисел вновь начинается с 1.  

Цифрами вавилонского числового метода считались клинья, разные для записи единиц, десятков и нуля.

Система счисления майя

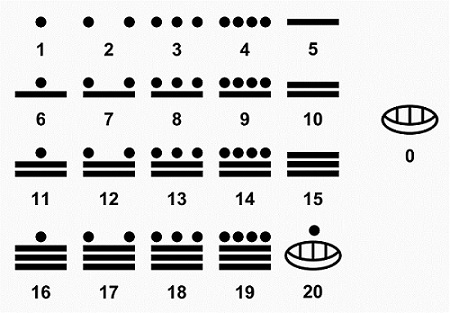
Рассматриваемый способ исчисления состоял из нуля и 19 сложных цифр. Ноль имел обозначение пустой ракушки. Цифры составлялись из точки и горизонтальной черточки. Точка означала единицу, черта – пятерку. 

Цифры майя применялась в календарных расчетах. В бытовых целях использовали непозиционный метод записи. Об этом свидетельствует то, что в позиционной системе счисления цивилизации майя имеется больше чисел, чем  необходимые 12.