Совершенная нормальная форма — дизъюнктивная и конъюнктивная, правило построения

Что такое СДНФ 

Нормальная форма логической формулы характеризуется тем, что для нее не свойственны эквивалентность, отрицание формул неэлементарного типа и знаки импликации.

Существует две формы нормального типа: КНФ (конъюнктивная нормальная форма) и ДНФ (дизъюнктивная нормальная форма).

ДНФ выглядит следующим образом:

\((A\;\wedge\;\overline B\;\wedge\;C)\;\vee\;(B\;\wedge\;C)\)

СДНФ обладает некоторыми определенными свойствами:

• включает различные элементарные конъюнкции;
• все логические слагаемые формулы содержат все переменные, которые входят в функцию F;
• ни в одном логическом слагаемом не содержится переменная и её отрицание.

К СДНФ возможно привести любую формулу алгебры логики. Исключение составляет только тождественно ложная формула. СДНФ можно получить как используя таблицы истинности, так и через равносильные преобразования.

Что такое СКНФ

КНФ имеет вид:

\((A\;\vee\;\overline B\;\vee\;C)\;\wedge\;(A\;\vee\;C)\)

Формула должна соответствовать нескольким условиям, чтобы называться СКНФ:

• в ней отсутствуют одинаковые элементарные дизъюнкции;
• дизъюнкции не содержат одинаковые переменные;
• все дизъюнкции содержат каждую переменную из входящих в конъюнктивную нормальную функцию такого типа.

Правила построения по таблице истинности

Дизъюнктивная форма

Если функция равна 1, то для всех наборов переменных, при которых это происходит, записывается произведение. Однако переменные, которые имеют значение 0, берутся с отрицанием.

Конъюнктивная форма

Когда функция равна 0, то для всех наборов переменных, при которых это происходит, записывается сумма. Однако переменные, которые имеют значение 1, берутся с отрицанием.

Алгоритм приведения к СДНФ и СКНФ

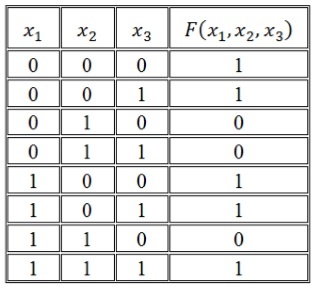
Рассмотрим логическую функцию в виде таблицы истинности.

Алгоритм построения СДНФ по таблице истинности выглядит следующим образом:

1. Отметить наборы переменных, значение функции F на которых равно 1.
2. Записать для всех отмеченных наборов конъюнкцию всех переменных так: если значение некоторой переменной в этом наборе равняется 1, в конъюнкцию включается сама переменная. В случае противного результата, в конъюнкцию включается ее отрицание.
3. Связать полученные конъюнкции операциями дизъюнкции.

Построим совершенную ДНФ:

И как результат получим следующую СДНФ:

\(F(x_1,\;x_2,\;x_3)\;=\;(\overline{x_1}\wedge\overline{x_2}\wedge\overline{x_3})\;\vee(\overline{x_1}\;\wedge\;\overline{x_2}\;\wedge\;x_3)\;\vee(x_1\;\wedge\;\overline{x_2}\;\wedge\;\overline{x_3})\;\vee\;(x_1\;\wedge\;\overline{x_2}\;\wedge\;x_3)\;\vee\;(x_1\;\wedge\;x_2\;\wedge\;x_3)\)

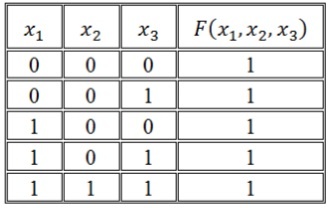
Алгоритм построения СКНФ по таблице истинности выглядит следующим образом:

1. Отметить в таблице истинности наборы переменных, значение функции F на которых равно 0.
2. Записать для всех отмеченных наборов дизъюнкцию всех переменных — в том случае, когда значение некоторой переменной в этом наборе равняется 0, в дизъюнкцию включается сама переменная, если происходит наоборот, то в дизъюнкцию включается ее отрицание.
3. Связать полученные дизъюнкции операциями конъюнкции.

Построим совершенную КНФ:

И как результат получим следующую СКНФ:

\(F(x_1,\;x_2,\;x_3)\;=\;(x_1\;\vee\;\overline{x_2}\;\vee\;x_3)\;\wedge\;(x_1\;\vee\;\overline{x_2}\;\vee\;\overline{x_3})\;\wedge\;(\overline{x_1}\;\vee\;\overline{x_2}\;\vee\;x_3)\)

Рассмотрев алгоритмы построения СДНФ и СКНФ ясно, что в случае подавляющей части наборов значений переменных функция равна 0, то значительно легче построить и СДНФ для получения ее формулы, а в обратном случае — СКНФ.

Доказательство эквивалентности

Доказать эквивалентность формул можно двумя способами.

1. Первый заключается в построении и сравнении таблиц истинности обеих функций. В этом случае результат будет истинным только в том случае, когда оба высказывания либо ложны, либо истинны.
2. Второй вариант — метод эквивалентных преобразований. Суть этого метода —  построение цепи эквивалентных формул на основе ранее доказанных эквивалентностей. 

Далее следуют примеры с некоторыми эквивалентными преобразованием в булевой алгебре и новыми эквивалентностями, которые возможно получить с их помощью. 

Поглощение

\(x\;\vee\;xy\;=\;x\)

\(x(x\;\vee\;y)\;=\;x\;\)

Доказательство эквивалентности:

\(x\;\vee\;xy\;=\;x\;\cdot\;l\;\vee\;xy\;=\;x(l\;\vee\;y)\;=\;x\)

\(x(x\;\vee\;y)\;=\;xx\;\vee\;xy\;=\;x\;\vee\;xy\;=\;x\)

Склеивание

\(xy\;\vee\;x\overline y\;=\;x\)

Доказательство эквивалентности:

\(xy\;\vee\;x\overline y\;=\;x(y\;\vee\;\overline y)\;=\;x\;\cdot\;l\;=\;x\)

Обобщенное склеивание

\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\)

Доказательство эквивалентности

\(xz\;\vee\;y\overline z\;\vee\;xy\;=\;xz\;\vee y\overline z\;\vee\;xyz\;\vee\;xy\overline z\;=\;xz\;\vee\;y\overline z\)

Расщепление

\(x\;\vee\;\overline xy\;=\;x\;\vee\;y\)

Доказательство эквивалентности

\(x\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;\overline xy\;=\;xy\;\vee\;x\overline y\;\vee\;xy\;\vee\;\overline xy\;=\;x\;\cdot\;l\;\;\vee\;y\;\cdot\;l\;=\;x\;\vee\;y\)

Примеры с решением

Задача №1

Приведите к СКНФ \(((((A\rightarrow B)\rightarrow\overline A)\rightarrow\overline B)\rightarrow\overline C)\).

Через применение закона де Моргана и правила\( x\;\rightarrow\;y\;=\;\overline x\;\vee\;y\) упростим выражения:

\(F\;=\;((((A\;\rightarrow\;B)\;\rightarrow\;\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;(((\overline A\;\vee\;B)\;\rightarrow\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\overline C\;)\;=\)

\(=\;((((\overline A\;\vee\;B)\;\rightarrow\overline A)\;\rightarrow\overline B)\;\rightarrow\;\overline C)\;=\;((\overline{((\overline A\;\vee\;B)}\;\vee\;\overline A)\;\rightarrow\overline B)\;\rightarrow\overline C)\;=\)

\(=(((\overline A\;\vee\;B)\;\vee\;\overline A)\;\rightarrow\;\overline B)\;\rightarrow\;\overline C)\;=((\overline{(\overline{(\overline A\vee B)}\;\vee\;\overline A\;)}\;\vee\;\overline B)\;\rightarrow\;\overline C)\;=\)

\(=\;(\overline{(\overline{(\overline{(\overline A\;\vee\;B)}\;\vee\;\overline A)}\;\vee\;\overline B)}\;\vee\;\overline C)\;=\;(((A\;\vee\;B)\;\vee\;\overline A)\;\vee\;\overline B)\;\vee\;\overline C\;=\)

\(=\;((\overline{(\overline A\;\vee\;B)}\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge B)\;\vee\;\overline C\;=\)

\(=((A\overline B\;\vee\;\overline A)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=(((A\;\wedge\;\overline B)\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\)

\(=\;((A\overline B\;\vee\;\overline A)\;\wedge\;B)\;\vee\;\overline C\;=\;(A\overline BB\;\vee\;\overline AB)\;\vee\;\overline C\;=\;(0\;\vee\;\overline AB)\;\vee\;\overline C\;=\;\overline AB\;\vee\;\overline C\)

Далее приведем выражение к КНФ:

\(F\;=\;\overline AB\;\vee\;\overline C\;\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\)

Далее приведем выражение к СКНФ:

\(F\;=\;(\overline A\;\vee\;\overline C)\;\wedge\;(B\;\vee\;\overline C)\;=\;(\overline A\;\vee\:\overline C\;\vee\;B\overline B)\;\wedge\;(A\overline A\;\vee\;B\;v\;\overline C)\;=\)

\(=\;(\overline A\;\vee\;\overline C\;\vee\;B)\;\wedge\;(A\;\vee\;B\;\vee\;\overline C)\;\wedge\;(\overline A\;\vee\;\overline C\;\vee\;\overline B)\;\wedge\;(\overline A\;\vee\;B\;\;\overline C)\)

Задача №2

Используя эквивалентные преобразования, постройте ДНФ функции \(f(\widetilde x^n)\)

\(f(\widetilde x^3) = (\overline{x_1}x_2\;\oplus\;x_3)\;\cdot\;(x_1x_3\;\rightarrow\;x_2)\)

Преобразуем функцию:

\(f(\widetilde x^3) = (\overline{x_1}x_2\;\oplus\;x_3)\;\cdot\;(x_1x_3\;\rightarrow\;x_2) = ((\overline{x_1}x_2\;\cdot\;\overline{x_3}\;)\;\vee\;(\overline{\overline{x_1}x_2}\;\cdot\;x_3))\;\cdot\;(\overline{x_1x_3}\;\vee\;x_2)\;=\)

\(=\;((\overline{x_1}x_2\overline{x_3})\;\vee\;((\overline{\overline{x_1}}\;\vee\;\overline{x_2})\;x_3)\;\cdot\;(\overline{x_1}\;\vee\;\overline{x_3}\;\vee\;x_2)\;=\;((\overline{x_1}x_{2\;}\overline{x_3})\;\vee\;((x_1\;\vee\;\overline{x_2})\;x_3)\;\cdot\;(\overline{x_1}\;\vee\;\overline{x_3}\;\vee\;x_2)\;=\)

\(=\;(\overline{x_1}x_2\overline{x_3}\;\vee\;x_1x_3\;\vee\;\overline{x_2}x_3)\;\cdot\;(\overline{x_1}\;\vee\;\overline{x_3}\;\vee\;x_2)\;=\)

\(=(\overline{x_1}x_2\overline{x_3}\;\cdot(x_1\vee x_3\vee x_2)\;\vee\;x_1x_3\;\cdot\;(\overline{x_1}\;\vee\;\overline{x_3}\;\vee\;x_2)\;\vee\;\overline{x_2}x_3\;\cdot\;(\overline{x_1}\;\vee\;\overline{x_3}\;\vee\;x_2))\;=\)

\(=\;(\overline{x_1}x_2\overline{x_3}\;\vee\;(x_1\;x_3\overline{x_1}\;\vee\;x_1x_3\overline{x_3}\;\vee\;x_1x_3x_2)\;\vee\;(\overline{x_2}x_3\overline{x_1}\;\vee\;\overline{x_2}x_3\overline{x_3}\;\vee\;\overline{x_2}x_3x_2)\;=\)

\(=\;(\overline{x_1}x_2\overline{x_3}\;\vee\;0\;\vee\;0\;\vee\;x_1x_2x_3\;\vee\;\overline{x_1}\overline{x_2}x_3\;\vee\;0\;\vee\;0)\;=\)

\(=\;\overline{x_1}x_2\overline{x_3}\;\vee\;x_1x_2x_3\;\vee\;\overline{x_1}\overline{x_2}x_3\)