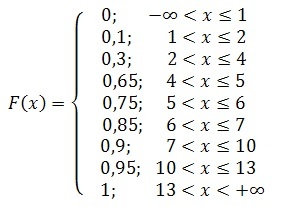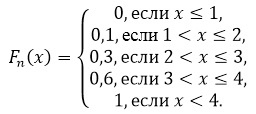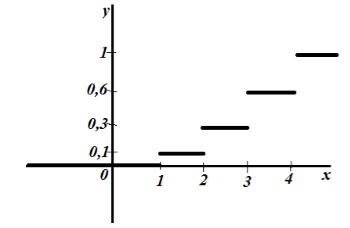Эмпирическая функция распределения

Что называют эмпирической функции распределения

Допустим, известно статистическое распределение частот количественного признака Х. Обозначим n_х – количество наблюдений со значением меньше x₁, n – всего наблюдений. Очевидно, что относительная частота события Х<x будет равна n_х/n.

Данное понятие можно записать в виде формулы:

\(F\ast(x)=\frac{n_x}n\)

В этой записи n_x – количество вариантов, меньших x; n – объем выборочной совокупности.

Существует также теоретическая функция распределения (функция распределения генеральной совокупности). Ее отличие от выборочной функции распределения состоит в определении объективной возможности или вероятности события X<x.

Свойства функции

Функция распределения выборки обладает рядом свойств, которые следуют из определения понятия.

1. Значения рассматриваемой функции F^*(x) располагаются на отрезке [0; 1].
2. Функция имеет неубывающий характер.
3. При минимальной варианте x₁ верно равенство F^*(x)=0 при условии, что х<х₁. При максимальной варианте х_k верно равенство F^*(x)=1 при условии х>x_k.

Таким образом, функция распределения выборки помогает оценить теоретическую функцию распределения.

Как найти

Выборочная функция распределения для случайной величины рассчитывается по формуле:

\(F(x)=P(\xi<x)\)

Данное равенство читается так: функция распределения равна вероятности события, при котором случайная величина будем меньше x.

Поскольку при условии, что x меньше или равно 1, событие ξ₂₀<1 невозможно (ξ₂₀ не принимает значение менее 1, вероятность невозможного события равна 0), верно следующее выражение:

\(F(x)=P(\xi20<1)=0\)

При принадлежности x отрезку (1; 2] событие ξ₂₀<2 представляет собой равенство ξ₂₀=1, значит, вероятность этого события равно 0,1. В записи это выглядит так:

\(F(x)=P(\xi20<2)=0,1\)

Когда x принадлежит отрезку (2; 4], событие ξ₂₀<4 состоит в равенстве ξ₂₀ значению 1 или 2, то есть вероятность рассматриваемого события равна 0,1+0,2=0,3 или:

\(F(x)=P(\xi20<4)=0,3\)

Если 4 < x ≤ 5, то событие ξ₂₀<5 означает, что ξ₂₀ принимает значение либо 1, либо 2, либо 4. Следовательно, вероятность данного события вычисляется так: 0,1+0,2+0,35=0,65, то есть:

\(F(x)=P(\xi20<5)=0,65\)

При 5 < x ≤ 6 событие ξ₂₀<6 заключается в том, что ξ₂₀ принимает значение 1, 2, 4 или 5. Значит его вероятность равно 0,1+0,2+0,35+0,1=0,75 или:

\(F(x)=P(\xi20<6)=0,75\)

И так далее.

Итак, эмпирическая функция распределения имеет следующий вид:

Как построить график

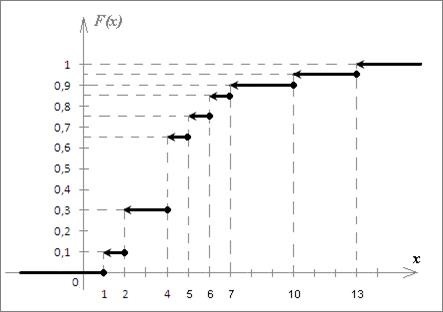
Построение графика эмпирической функции распределения возможно после вычисления ее значений на всей числовой оси. Для рассмотренного примера схематическое изображение будет выглядеть так:

График ступенчатого вида, построенный на отрезках. Совпадение графика с горизонтальной осью означает, что левее минимального значения x=1 функция приобретает значение нуля. Увеличение в каждой следующей точке x_i происходит на величину вероятности ν_i. Правее максимального значения х₈=13 функция равна 1. Стрелки и точки на концах отрезков указывают на определение функции на полуинтервалах.

Примеры задач

Задача

В таблице даны значения эмпирического распределения:

Необходимо найти объем выборочной совокупности, составить выборочную функцию распределения, построить ее график.

Решение

1. Вычислим объем выборки: n=5+10+15+20=50.
2. Из свойства эмпирической функции распределения: F_n(x)=0 при x≤1, F_n(x)=1 при x>4.

Выходит, что:

По полученным значениям построим график: