Элементарные функции

Что такое элементарные функции в высшей математике

Основу для их вычисления в теории математического анализа их принято называть простейшими или основными элементарными функциями.

Основные элементарные функции, классификация

Основные элементарные функции — базисные функции для вычисления последующих. Ниже приведен список их видов:

• степенные;
• показательные;
• логарифмические;
• тригонометрические;
• обратные тригономестрические.

Каждая из них делится на отдельные типы. Рассмотрим характеристику каждого и построение соответствующего графика.

Степенные 

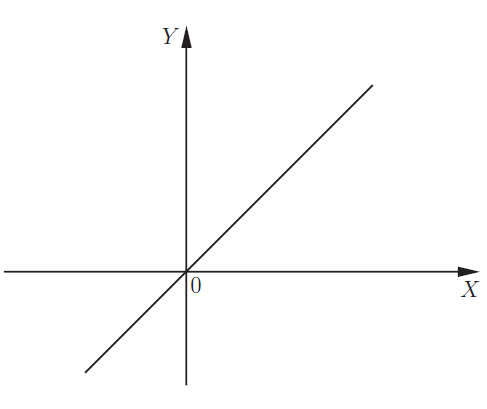
Линейная: \(y=kx + b\). Функция представляет собой линейную зависимость и является прямой.

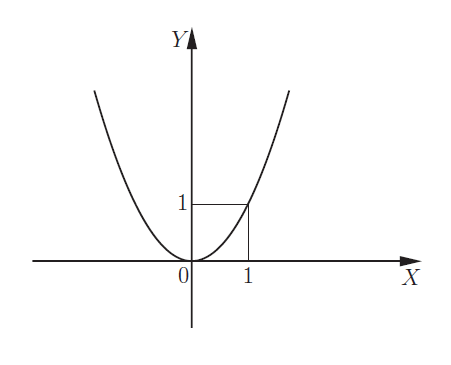
Квадратичная: \(y = ax2 + bx + c\). Симметрична, показывает квадратичную зависимость. Графически изображается как парабола:

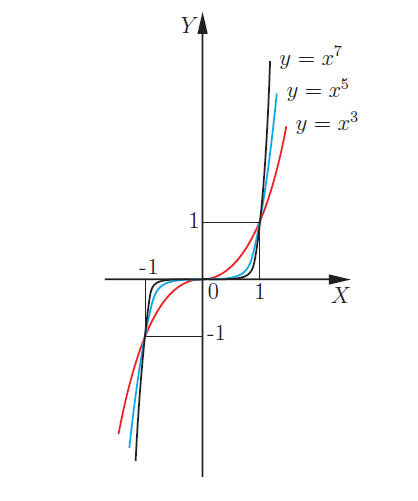
Степенная кубическая: \(y = kx3\). Пример нечетной степени функции — кубическая парабола:

  

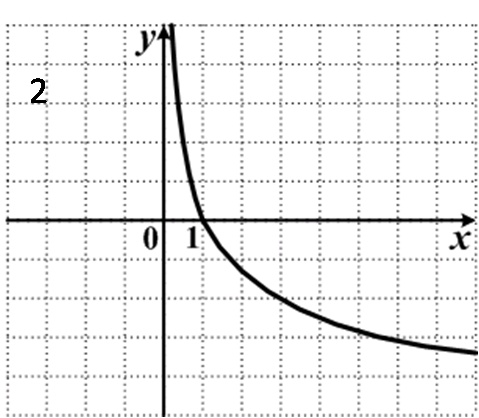
Дробная: \(y = k/x\). Отображает обратно-пропорциональную зависимость и носит название гипербола:

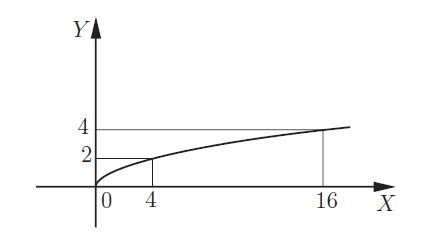
Дробная степень: \(y = √x = x1/2\). Формулой такой зависимости является вычисления арифметического корня:

Показательные 

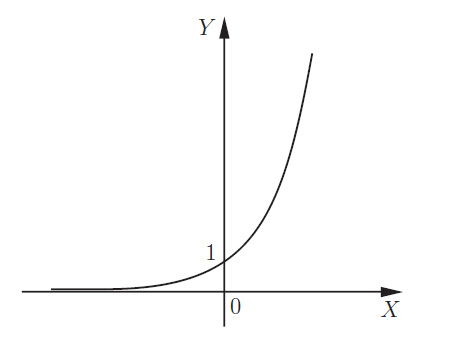
Для иррационального числа \( (е≈2,7182818284590...): y = ex.\) Если основанием является иррациональное число, то график обозначается понятием экспонента: 

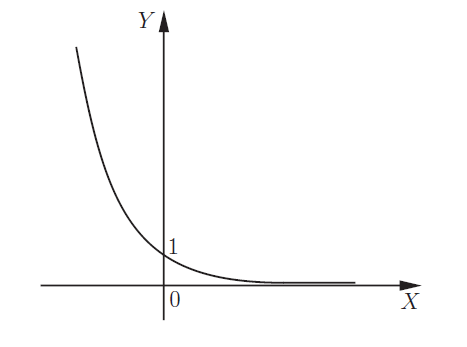
В остальных случаях принимает вид \(y = ax\) и ее свойства зависят от числового промежутка, к которому принадлежит показатель а. Например, если \(0 < a < 1\), то:

Логарифмическая 

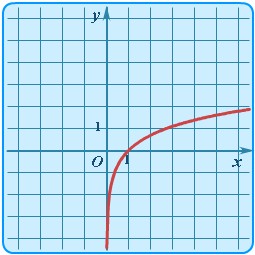
Логарифмика: \(y = lnx\). Натуральный логарифм (за основание принимается иррациональное число e):

В остальных случаях формула будет записываться, как: \(y = logax\). И построение графика будет зависеть от параметра a:

  

Тригонометрические 

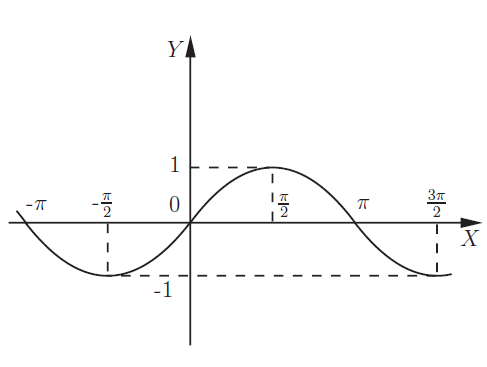
Синус: функция для значений \(y=sinx\), и ее график синусоида:

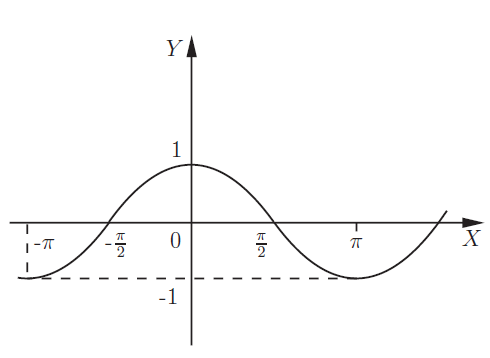
Косинус: значения \(y=cosx\), и изображение этой зависимости называется косинусоида:

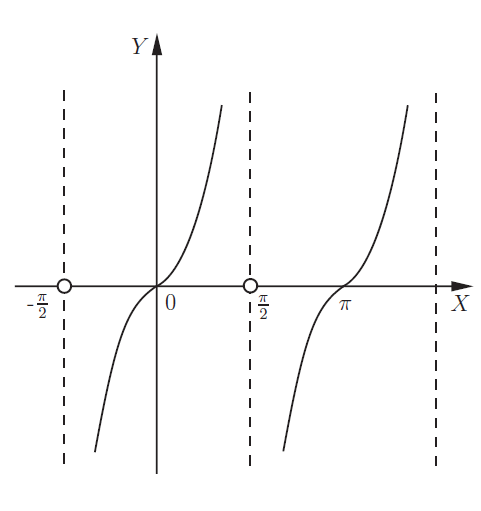
Тангенс: уравнение тригонометрической функции: \(y=tgx\) графически представляет собой тангенсоиду:

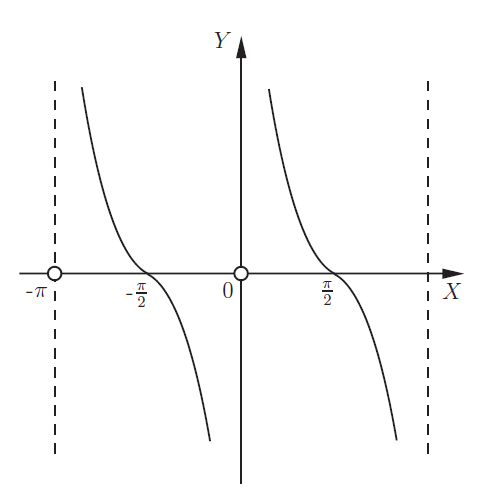
Котангенс, для формулы:\( y=ctgx \)— котангенсоидой:

Обратные тригонометрические 

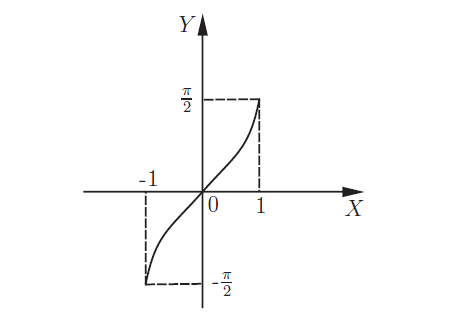
Арксинус: выражение обратное y=sinx записывается как \(y=arcsinx\) и изображается арксинусоидой соответственно: 

Арккосинус: так называется функция обратная y=cosx. Ее формула — \(y=arccosx\), а изображающая ее кривая — арккосинусоида:

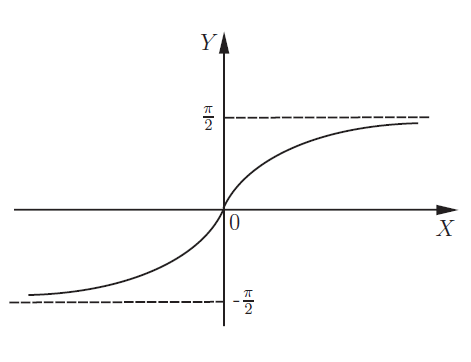
Арктангенсс: данный пример характерен и для \( y=tgx.\) Получаем  \(y=arctgx\) и арктангенсоиду:

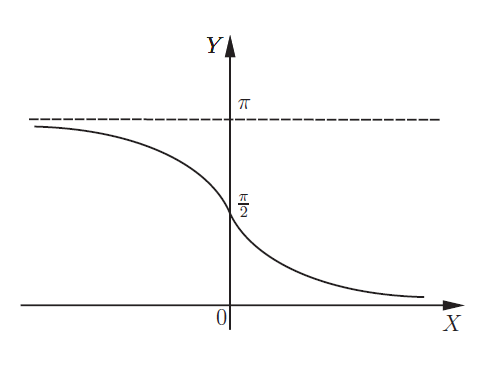
Арккатангенс: для \(y=arcctgx\) график будет называться арккотангенсоида и выглядеть так:

Вычисление элементарных функций

Для вычисления элементарных функций используются следующие методы:

1. Ряд Тейлора (разложение элементарной функции в бесконечную сумму степенной). Комплексный подход, один из наиболее используемых.
2. Аппроксимацию с помощью полиномов, т.е. замену одних элементов другими.
3. Табличный метод.
4. Рациональные приближения.
5. Цепные дроби (бесконечные математические выражения. Решение находится посредством их исследования).
6. Итерация (нахождение приближения по предыдущему приближённому значению).