Функция Кобба-Дугласа

Что такое функция Кобба-Дугласа

Впервые данное понятие теоретически предложил шведский экономист Кнут Викселль.

В 1928 году американские ученые Чарльз Кобб и Пол Дуглас в своем труде «Теория производства» проверили функцию на практике, а именно на статистической информации. В данной работе экономисты попытались опытным путем установить зависимость объема продукции, выпускаемой обрабатываемой промышленностью США, от вложенного капитала и труда.

Общий вид функции

Рассматриваемая функция выглядит следующим образом:

\(Q=A\times L^\alpha\times K^\beta\)

В данной формуле:

• Q — это объем производства.
• A — это технологический коэффициент, то есть совокупность влияющих на выпуск продукции факторов, кроме труда и капитала.
• L — трудовые затраты.
• α≥0 — коэффициент эластичности (меры чувствительности одного параметра к изменению другого) по труду.
• K — вложенный капитал.
• β≥0 — коэффициент эластичности по капиталу.

Функция Кобба–Дугласа считается линейно однородной, когда при сложении степеней α+β получается единица. В этом случае масштабы производства меняются, а отдача присутствует постоянно.

Если при сложении коэффициентов эластичности по труду и капиталу получается величина больше единицы, то отдача производства увеличивается. При α+β<1 отдача уменьшается.

Разновидности функции

Однофакторная производственная функция

Данный термин применяется в описании производственного процесса в краткосрочном периоде. В этом случае совокупный продукт Q испытывает влияние только одной переменной при постоянстве других факторов. Чаще всего труд L является переменным фактором.

\(Q=f(L)\)

Переменным фактором также могут быть капитал K или земля M.

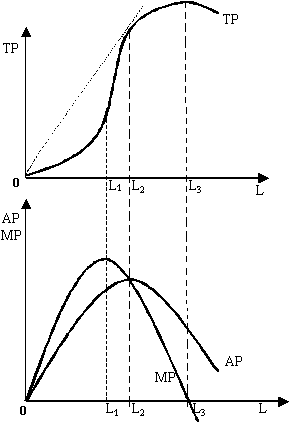
Однофакторная производственная функция имеет следующий вид:

На верхнем изображении видна динамика выпуска продукции TP при переменном факторе труда L. На нижнем графике представлена характеристика изменения средней производительности AP и предельной производительности MP переменного производственного фактора.

\(AP\) — это количество продукции, приходящееся на единицу переменного фактора.

Средний продукт труда AP_L вычисляется по формуле:

\(AP_L=\frac{TP_L}L\)

MP демонстрирует рост выпуска продукции при условии, что переменный фактор производства возрастет на бесконечно малую величину. Предельный продукт представлен в виде формулы, которая является производной однофакторной производственной функции:

\(MPL\;=\;Q'(L)\)

В производственной функции, заданной в виде таблицы, MP_L — это величина прироста объема производства при возрастании переменного фактора производства на 1:

\(MPL\;=\;⌂Q/\;⌂L.\)

Двухфакторная производственная функция

При одновременном изменении двух факторов производства и константе третьего фактора образуется двухфакторная производственная функция. В качестве переменных и постоянных могут выступать разные факторы. Наиболее часто встречается ситуация, когда на объем производства влияют переменные фактора труда и капитала.

Математически эта зависимость выглядит так:

\(Q\;=\;f\;(К,\;L)\)

Особенности функции

Функция Кобба–Дугласа состоит из двух ключевых факторов, которые включены в производство: труд и капитал. Пропорциональное соотношение данных составляющих является условием создания продукта. Рассматриваемая функция служит отражением технологического соотношения труда и капитала, как обязательных факторов производства любого товара в определенном объеме.

В узком понимании термин «функция Кобба–Дугласа» обозначает зависимость постоянной отдачи от масштаба. 

Производственная функция, названная в честь экономистов Кобба и Дугласа — это первая функция обобщенного производства. Использование данного понятия позволяет создавать модели не только процессов небольших масштабов, но и целых отраслей экономики. Эмпирическое подтверждение рассматриваемой функции стало толчком в макроэкономическом развитии, благодаря чему появилась возможность оценивать производственную эффективность национального хозяйства.

Примеры использования функции

Вычислить:

• максимальное количество выпускаемой продукции;
• средний продукт труда;
• объем выпускаемой продукции при увеличении труда и капитала вдвое.

Решение:

Выпустить максимум продукции возможно только при условии максимального использования труда и капитала, то есть:

\(Qmax=40,5\times40,5=4.\)

Средний продукт труда \(ATL\) равен соотношению объема производства к количеству затрачиваемого труда, то есть:

\(ATL=Q/L=4/4=\;1.\)

При увеличении производственных факторов труда и капитала в два раза максимальный объем выпускаемой продукции будет равен:

\(Qmax=80,5\times80,5=8.\)

Необходимо найти:

1. Предельные продукты труда и капитала при\( K=16\), \(L=125\).
2. Коэффициенты эластичности по труду и капиталу, экономически расшифровать полученные значения.

Решение:

\(MQL\) — прирост объема производства при увеличении труда на 1:

\(MQ_L=\frac{dQ}{dL}=150\times0,5K^{0,9}\times L^{-0,5}=\frac{75K^{0,9}}{\sqrt L}\)

При заданных условиях \(K=16\), \(L=125\) искомая величина \(MQL\) равна:

\(MQ_L=\frac{75K^{0,9}}{\sqrt L}=\frac{75\times16^{0,9}}{\sqrt{125}}=\frac{75\times\sqrt[10]{16^9}}{\sqrt{5\times25}}=\frac{75\times\sqrt[10]{{(2^4)}^9}}{5\sqrt5}=\frac{15\times\sqrt[10]{2^{36}}}{\sqrt5}=\frac{15\times\sqrt[10]{2^{30}}\times\sqrt[10]{2^6}}{\sqrt5}=\frac{15\times2^3\times\sqrt[5]{2^3}}{\sqrt5}=\frac{15\times8\times\sqrt[5]8}{\sqrt5}=\frac{120\sqrt[5]8}{\sqrt5}\approx81,342\)

Вычислим предельный продукт капитала \(MQK:\)

\(MQ_K=\frac{dQ}{dK}=150\times0,9K^{-0,1}\times L^{0,5}=135\frac{\sqrt L}{\sqrt[10]K}=135\frac{\sqrt{125}}{\sqrt[10]{16}}=135\frac{\sqrt{5\times25}}{\sqrt[10]{2^4}}=135\frac{5\sqrt5}{\sqrt[5]{2^2}}=\frac{675\sqrt5}{\sqrt[5]4}\approx1143,9\)

Поскольку частные производные больше нуля, увеличение любых затрат не влечет уменьшение выпуска продукции.

Для производственной функции вида \(Q=150K0,9\times L0,5\) коэффициент эластичности по труду α определяется по формуле:

\(E_L(Q)=\frac{\displaystyle\frac{dQ}{dL}}{\displaystyle\frac QL}=\frac{150\times0,5K^{0,9}\times L^{-0,5}}{\displaystyle\frac{150K^{0,9}\times L^{0,5}}L}=\frac{0,5K^{0,9}\times L^{-0,5}}{K^{0,9}\times L^{0,5-1}}=0,5\frac{K^{0,9}\times L^{-0,5}}{K^{0,9}\times L^{-0,5}}=0,5\;=\alpha\)

Коэффициент по капиталу β вычислим следующим образом:

\(E_K(Q)=\frac{\displaystyle\frac{dQ}{dK}}{\displaystyle\frac QK}=\frac{150\times0,9K^{-0,1}\times L^{0,5}}{\displaystyle\frac{150K^{0,9}\times L^{0,5}}K}=\frac{0,9K^{-0,1}\times L^{0,5}}{K^{0,9-1}\times L^{0,5}}=0,9\frac{K^{-0,1}\times L^{0,5}}{K^{-0,1}\times L^{-0,5}}=0,9\;=\beta\)

При \(α=0,5\) увеличение трудовых затрат на 1 % приведет к росту производственного объема на 0,5 %.

При \(β=0,9\) увеличение вложенного в процесс производства капитала на 1 % повлечет за собой рост объема производства на 0,9 %.

При сложении коэффициентов α и β получится 1,4, то есть сумма \(α + β\) больше единицы. Это означает, что производственная функция непропорционально возрастающая. В данном случае эффективность факторов производства растет, то есть при увеличении затрат \(K\) и\( L\) в некоторой пропорции наблюдается рост объема производства \(Q\) в большей пропорции.

Если речь идет о конкурентном рынке, то величины α и β характеризуют прогнозируемые доли дохода, полученного за счет труда и капитала соответственно. На конкурентном рынке труда ставка зарплаты w соответствует предельному продукту труда:

\(w=MQ_L=\frac{dQ}{dL}=\frac{\alpha Q}L=81,342\)

Значит, итоговая сумма зарплаты wL будет равна \(αQ\). Трудовая доля в общем выпуске \(wL/Q\) будет постоянной величиной \(α=0,5.\)

Норма прибыли определяется аналогично через \(dQ/dK:\)

\(\rho=MQ_K=\frac{dQ}{dK}=\frac{\beta Q}K=1143,9\)

Отсюда следует, что итоговая прибыль \(ρQ\) равна \(βQ\). Константа \(β=0,9\) является долей прибыли \( ρK/Q.\)