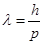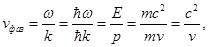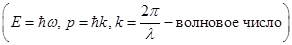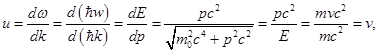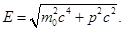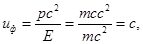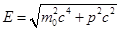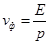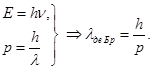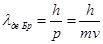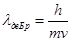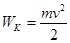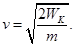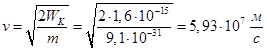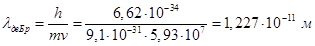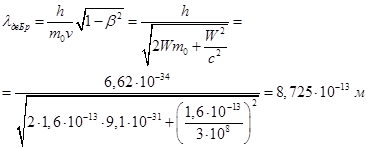Как определить длину волны де Бройля для электрона

Волна де Бройля или волна амплитуды вероятности

Согласно определения волн де Бройля, можно сделать вывод об их взаимодействии с какими-либо частицами и их волновой природе. Формулировка волн материи была введена в науку в 1924 году французским физиком-теоретиком Луи де Бройлем. Благодаря теории, свойство корпускулярно-волнового дуализма (или двойственности) было распространено на любые проявления материи, включая излучение и какие-либо частицы вещества.

В современной квантовой теории «волна материи» понимается несколько иначе. Однако название данного физического феномена, связанного с частицами вещества, включая водород, сформулировано в честь автора гипотезы.

В 1913 году Н. Бор предложил полуклассическую модель атома, в основе которой было два постулата:

1. Момент импульса электрона в атоме строго определен. Величина в любом случае пропорциональна nh/2π, где n – какое-либо целое число, начиная с 1, а h – постоянная Планка, присутствие которой в формуле ясно свидетельствует о том, что момент импульса частицы квантован. Таким образом, атом включает комплекс разрешенных орбит, по которым только и может перемещаться электрон. Когда электрон расположен на этих орбитах, излучение (то есть потеря энергии) отсутствует.
2. Атомный электрон излучает или поглощает энергию в процессе перехода с одной орбиты на другую в количестве, определяемом, как разность энергий на этих орбитах. В связи с тем, что промежуточные состояния между разрешенными орбитами отсутствуют, излучение строго квантуется. Показатель его частоты составляет (E1 – E2)/h, что является выводом из формулы Планка для энергии E = hν.

Таким образом, боровская модель атома не предусматривает излучение электрона на орбите, его нахождение между орбитами. Однако согласно простой рассматриваемой модели, движение электрона рассматривают с классической точки зрения, как вращение планеты вокруг Солнца.

В процессе поиска ответа на вопрос о поведении электрона Де Бройль предположил, что электрону в любом случае должна соответствовать определенная волна. Благодаря ей, частица «выбирает» исключительно такие орбиты, на которых данная волна укладывается целое число раз. В этом и заключался смысл целочисленного коэффициента в постулированной Бором формуле.

Гипотеза приводит к выводу, что электронная волна де Бройля не является электромагнитной, а волновые параметры должны быть характерны для любых материальных частиц, а не только для электронов в атоме. Ученому удалось получить важное соотношение, с помощью которого можно определить тип этих рассматриваемых волновых свойств. Формула расчета волны де Бройля:

\(λ = h/p\)

где λ – является длиной волны, p – определяет импульс частицы в уравнении.

Де Бройль объединил в одном соотношении корпускулярную и волновую характеристики материи: такие, как импульс и длина волны. Данные параметры связывает постоянная Планка, величина которой примерно составляет \(6,626*10^{-27} эрг∙с\) или \(6,626*10^{-34} Дж∙с\), задающая масштаб проявления волновых свойств вещества.

Природа волн де Бройля, фазовая и групповая скорость

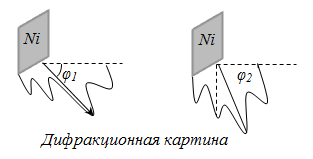
Следует отметить, что волны де Бройля, называемые электронными волнами, не являются электромагнитными. В 1927 году американским физикам Дэвиссону и Джермеру удалось подтвердить гипотезу де Бройля. Ученые обнаружили дифракцию электронов на кристалле никеля. В процессе получилось определить дифракционные максимумы, которые соответствуют формуле Вульфа-Брэггов:

\(2dsinj = nl\)

Расчет брэгговской длины волны подтвердил ее соответствие формуле:

В дальнейшем гипотеза де Бройля была подтверждена опытным путем Л.С. Тартаковским и Г. Томсоном. Ученым удалось зафиксировать дифракционную картину, когда пучок быстрых электронов при Е≈ 50 кэВ проходит сквозь фольгу из разных металлов.

Чуть позже получилось обнаружить дифракцию нейтронов, протонов, атомных пучков и молекулярных пучков. В дальнейшем были изобретены инновационные методики исследования вещества, включая нейтронографию и электронографию, сформировалось направление электронной оптики.

Макротела должны характеризоваться аналогичными свойствами. В случае, если m = 1кг,  \(l = 6,62*10^{-31} м\) – невозможно обнаружить современными методами – поэтому макротела рассматриваются только в качестве корпускул.

В том случае, когда частица с массой m перемещается со скоростью v, фазовая скорость волн де Бройля будет определяться по формуле:

Исходя из того, что c > v, фазовая скорость волн де Бройля превышает скорость света в вакууме. Можно отметить, что фазовая скорость Vф может быть больше и может быть меньше с, в отличие от групповой скорости. Формула групповой скорости:

Таким образом, групповая скорость волн де Бройля соответствует скорости движения частицы. В случае фотона она будет равна:

В результате, значение групповой скорости равно скорости света.

Волны де Бройля подвержены дисперсии. Если подставить выражение:

в формулу:

получим следующее равенство:

\(Vф= f(λ)\)

Какой формулой определяется длина волны

Количественные соотношения, которые связывают корпускулярные и волновые способности частиц, аналогичны свойствам фотонов:

Гипотеза де Бройля основана на универсальном характере данного равенства, что справедливо в условиях любых волновых процессов. Какой-либо частице, которая обладает импульсом р, соответствует волна. Ее длину можно определить с помощью формулы де Бройля:

p =mv- является импульсом частицы, h – определяется, как постоянная Планка.

Как определить длину волны де Бройля для электрона

Рассчитать длину волны де Бройля для электрона можно на конкретном примере. Предположим, то требуется определить длину волны де Бройля λ для электрона, кинетическая энергия которого составляет:

• W1 = 10 кэВ;
• W2 = 1 МэВ.

В первую очередь стоит записать исходные данные:

\(m_{e}=9,1*10^{-31} кг\)

\(W1 = 10 кэВ = 10*10^{3}*1,6*10^{-19} = 1,6*10^{-15}Дж\)

\(W2 = 1 МэВ = 10*10^{6}*1,6*10^{-19}= 1,6*10^{-13} Дж\)

Требуется найти λ.

Решение:

Формула волны де Бройля:

Так как известна кинетическая энергия электронов, можно рассчитать их скорость:

 Далее можно определить длину волны де Бройля:

В том случае, когда скорость v частиц соизмерима со скоростью света с, длину волны де Бройля можно рассчитать по формуле: