Движение тела, брошенного под углом к горизонту

Что такое движение тела брошенного под углом к горизонту

В процессе подбрасывания объекта вверх под углом к горизонту вначале наблюдают его равнозамедленный подъем, а затем равноускоренное падение. Скорость перемещения тела, относительно поверхности земли, остается постоянной.

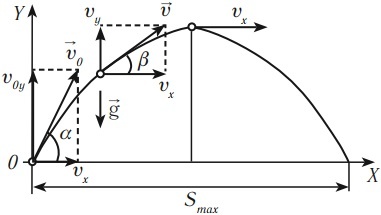
На графике изображено схематичное движение тела, которое подбросили под углом к горизонту. В этом случае α является углом, под которым объект начал свое перемещение. Характеристики такого процесса будут следующими:

1. Направление вектора скорости тела, которое подбросили под определенным углом к горизонту, будет совпадать с касательной к траектории его перемещения.
2. Начальная скорость отличается от направления горизонтальной линии, а обе ее проекции не равны нулю.
3. Проекция скорости в начале движения на ось ОХ составляет \(V_{ox}=V_{0}\cos \alpha\).
4. Проекция начальной скорости на ось ОУ равна \(V_{oy}=V_{0}\sin \alpha\).
5. Проекция мгновенной скорости на ось ОХ следующая: \(V_{x}=V_{0}\cos \alpha\).
6. Проекция мгновенной скорости на ось ОУ обладает нулевым значением и рассчитывается следующим образом: \(V_{x}=V_{0}\sin \alpha-gt\).
7. Ускорение свободного падения на ось ОХ обладает нулевой проекцией, или \(g_{x}=0\).
8. Проекция ускорения свободного падения на ось ОУ равна \(–g\), или \(g_{y}=-g\).

К числу кинематических характеристик движения тела, которое подбросили под углом к горизонту, относят модуль мгновенной скорости в определенное время t. Данный показатель можно рассчитать с помощью теоремы Пифагора:

\(V=\sqrt{V^{2}_{x}+V^{2}_{y}}\)

Минимальная скорость тела будет замечена в самой верхней точке траектории, а максимальная величина данной характеристики будет достигнута, когда объект только начинает перемещаться, а также в точке падения на поверхность земли. Время подъема представляет собой время, необходимое для достижения телом верхней точки траектории. За полное время объект совершает полет, то есть перемещается от начальной точки к точке приземления.

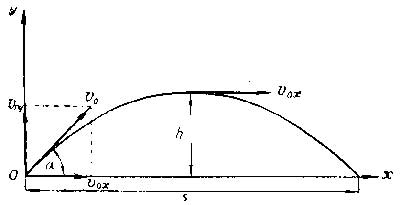
Дальность полета является перемещением объекта по отношению к оси ОХ. Такую кинематическую характеристику обозначают буквой l. По отношению к оси ОХ тело перемещается, сохраняя постоянство скорости.

Расчет горизонтального смещения тела в какой-либо момент времени t выполняют с помощью уравнения координаты х:

\(x=x_{0}+V_{0x}t+\frac{gxt^{2}}{2}\)

Зная следующие условия:

• \(x_{0}=0\);
• проекция ускорения свободного падения, относительно оси ОХ, также имеет нулевое значение;
• проекция начальной скорости на ось ОХ составляет \(V_{0}\cos \alpha\).

Записанная формула приобретает следующий вид:

\(x=V_{0}\cos \alpha t\)

Мгновенной высотой принято считать высоту, на которой находится объект в определенный момент времени t. Наибольшей высотой подъема является расстояние от поверхности земли до верхней точки траектории движения тела под углом к горизонту.

Вывод формулы, как найти угол и дальность полета

Перемещение объекта, который был брошен под углом к горизонту, необходимо изобразить с помощью суперпозиций, характерных для двух типов движений:

• равномерное горизонтальное движение;
• равноускоренное перемещение в вертикальном направлении с ускорением свободного падения.

Скорость тела будет рассчитываться таким образом:

\(v_{0x}=v_{x}=v_{0} \cos \alpha =const\)

\(v_{0y}=v_{0}\sin \alpha\)

\(v_{y}=v_{0}\sin \alpha-gt\)

Уравнение координаты записывают в следующем виде:

\(x=v_{0}\cos \alpha \times t\)

\(y=v_{0}\sin \alpha \times t-\frac{gt^{2}}{2}\)

В любое время значения скорости тела будут равны:

\(v=\sqrt{v_{x}^{2}+v_{y}^{2}}\)

Определить угол между вектором скорости и осью ОХ можно таким образом:

\(\tan \beta =\frac{v_{y}}{v_{x}}=\frac{v_{0}\sin \alpha -gt}{v_{0}\cos \alpha }\)

Время подъема на максимальную высоту составляет:

\(t=\frac{v_{0}\sin \alpha }{g}\)

Максимальная высота подъема будет рассчитана следующим образом:

\(h_{max}=\frac{v_{0}^{2}\sin ^{2}\alpha}{2g}\)

Полет тела будет длиться определенное время, которое можно рассчитать с помощью формулы:

\(t=\frac{2v_{0}\sin \alpha }{g}\)

Максимальная дальность полета составит:

\(L_{max}=\frac{v_{0}^{2}\sin 2\alpha }{g}\)

Примеры решения задач

В примерах, описывающих движение тела, на которое действует сила тяжести, следует учитывать, что а=g=9,8 м/с².

Задача 1

Небольшой камень был брошен с ровной горизонтальной поверхности под углом к горизонту. Необходимо определить, какова максимальная высота подъема камня при условии, что, спустя 1 секунду после его начала движения, скорость тела обладала горизонтальным направлением.

Решение

Направление скорости будет горизонтальным в верхней точке перемещения камня. Таким образом, время, за которое он поднимется, составляет 1 секунду. С помощью уравнения времени подъема можно представить формулу произведения скорости в начале полета на синус угла, под которым бросили камень:

\(V_{0}\sin \alpha =gt\)

Данное равенство следует подставить в уравнение для расчета максимальной высоты, на которую поднимется камень, и выполнить вычисления:

\(h=\frac{V_{0}\sin ^{2}\alpha }{2g}=\frac{(gt)^{2}}{2g}=\frac{gt^{2}}{2}=\frac{10\times 1}{2}=5\)

Ответ: максимальная высота подъема камня, который бросили под углом к горизонту, составляет 5 метров.

Задача 2

Из орудия выпустили снаряд, начальная скорость которого составляет 490 м/с, под углом 30 градусов к горизонту. Нужно рассчитать, какова высота, дальность и время полета снаряда без учета его вращения и сопротивления воздуха.

Решение

Систему координат и движение тела можно представить схематично:

Составляющие скорости, относительно осей ОХ и ОУ, будут совпадать во время начала движения снаряда:

\(V_{0x}=V_{0} \cos \alpha\) сохраняет стабильность значения в любой промежуток времени во время всего перемещения тела.

\(V_{0y}=V_{0}\sin \alpha\) будет меняться, согласно формуле равнопеременного движения \(V_{y}=V_{0}\sin \alpha-gt\).

В максимальной точке, на которую поднимется снаряд:

\(V_{y}=V_{0}\sin \alpha-gt_{1}=0\)

Из этого равенства следует:

\(t=\frac{V_{0\sin \alpha }}{g}\)

Полное время полета тела будет рассчитано по формуле:

\(t=2t_{1}=\frac{2V_{0}\sin \alpha }{g}=50\)

Высота, на которую поднимется снаряд, определяется с помощью уравнения равнозамедленного перемещения тела:

\(h=V_{0y}t_{1}-\frac{gt_{1}^{2}}{2}=\frac{V_{0}^{2}\sin ^{2}\alpha }{2g}=3060\)

Дальность полета снаряда будет рассчитана таким образом:

\(S=V_{0x}t=\frac{V_{0}^{2}\sin 2\alpha }{g}=21000\)

Ответ: высота составляет 3060 метров, дальность полета равна 21000 метров, время движения составит 50 секунд.