Как рассчитать энергию заряженного конденсатора

Что такое энергия заряженного конденсатора

Конденсатор состоит из двух проводников, разделенных слоем диэлектрика.

Простейший конденсатор — две металлические пластины-обкладки, расположенные параллельно, с тонкой прослойкой воздуха между ними. Когда заряды пластин противоположны по знаку, электрическое поле оказывается сосредоточено внутри конденсатора и почти не взаимодействует с внешним миром, что позволяет накапливать на пластинах заряд. Для описания работы, которую нужно затратить, чтобы разделить положительные и отрицательные заряды и полностью зарядить конденсатор, вводится понятие энергии.

Где сосредоточена, в каких единицах измеряется

Вся энергия конденсатора сосредоточена в электрическом поле его пластин. Единица измерения СИ — джоуль.

Чему равна энергия заряженного конденсатора

По какой формуле можно найти

Основная характеристика поля, напряженность, создаваемая одной из пластин, равна половине напряженности поля во всем конденсаторе. Заряд q, распределенный по поверхности одной пластины, находится в однородном электрическом поле другой. Потенциальную энергию заряда можно найти по формуле:

\(W_п\;=\;q\frac E2d\)

где Е — напряженность поля во всем конденсаторе, а d — расстояние между пластинами.

В этой формуле могут использоваться другие известные величины, например, разность потенциалов между пластинами, обозначаемая буквой U. Чтобы вычислить ее, нужно умножить напряженность поля Е на расстояние между пластинами d. Тогда формула для вычисления энергии будет иметь вид:

\(W_п\;=\;\frac{qU}2\)

Электроемкость изолированного проводника С равна отношению изменения заряда q к изменению потенциала проводника \(\varphi\). Ее можно найти по формуле:

\(С\;=\;\frac qU\)

Таким образом, для решения задач можно использовать три выражения:

\(W_п\;=\;\frac{qU}2\;=\;\frac{q^2}{2C}\;=\;\frac{CU^2}2\)

Эти формулы справедливы для любого конденсатора, не только для плоского. Если малыми порциями \(-\triangle q\) переносить отрицательный заряд с одной пластины на другую, поле внутри конденсатора будет совершать работу. Если порции заряда малы, для простоты расчетов можно предположить, что напряжение между пластинами не меняется. Тогда работа:

\(\triangle А = -\triangle qU\;=\;-\frac1Cq\triangle q\)

\(\triangle W_п\;=\;\frac1Cq\triangle q\)

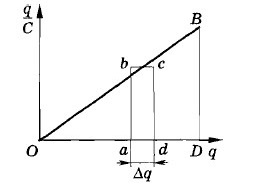
Построив график зависимости \(\;\frac qC\) от \(q\), мы видим, что приращение энергии численно равно площади прямоугольника \(abcd\) со сторонами \(\;\frac qC\triangle q\). Полное изменение энергии \(W_п \)будет равняться площади треугольника OBD.

Следовательно, \(W_{п\;}=\;\frac{OD\;\times\;DB}2\;=\;\frac{q^2}{2C}\).

Применение конденсаторов

Емкость конденсатора не слишком велика, но энергия при разрядке отдается почти мгновенно. Свойство конденсаторов быстро выдавать импульс большой мощности находит применение в лампах-вспышках для фотографирования, электромагнитных ускорителях, импульсных лазерах.Примером может служить генератор Ван де Граафа, позволяющий создавать в лабораторных условиях напряжение в миллионы вольт, чтобы моделировать разряды молний. Также конденсаторы используют в радиотехнике.

Существует тип компьютерных клавиатур, целиком состоящий из конденсаторов под каждой клавишей, при нажатии которой его пластины сближаются. Электронная схема, к которой они подсоединены, распознает, какую клавишу нажали, и передает эту информацию дальше.