Формула Ньютона-Лейбница для вычисления определенного интеграла

Что такое формула Ньютона-Лейбница

Сущность формулы Ньютона-Лейбница: применение

У традиционной трактовки формулы существует такая форма: 

В случае непрерывности функции \(f(x)\) на сегменте \([a,b]\) , а  \(Ф(x)\) является абсолютно любой первообразной на данной сегменте, получается такое выражение: \(\int_{a}^{b}f(x)dx=Ф(b)-Ф(a)=Ф(x)\mid_a^b\)

Доказательством данного выражения может являться следующая последовательность действий: 

Представим, что на отрезке [a, b] задается интегрируемая функция f (в зависимости от вида интеграла тип функции может меняться по своей сути). Далее нужно задать случайную величину вроде \(x\in[a,b]\). Потом необходимо дать определение введенной функции \(F(x)=\int_{a}^{x}f(t)dt\). Данная функция имеет определение для всех величин в рамках \(x\in[a,b]\). Такой порядок существует из-за того, что есть понимание того, что при существовании интеграла от f в сегменте [a, b], будет найден и интеграл, у которого f в сегменте [a, x]. Там уже наблюдается такая картина: \(a\leq{x}\leq{b}\). Необходимо сделать ремарку, что считается, исходя из дефиниции формулы Ньютона-Лейбница, что \(F(a)=\int_{a}^{a}f(t)dt=0\). Сделаем еще одну ремарку: \(F(b)=\int_{a}^{b}f(t)dt\). 

Теперь необходимо указать на то, что F будет беспрерывно располагаться в сегменте [a, b]. Для этого нужно произвести следующие вычисления. Представим, что \(x, x+h\in[a,b]\). В таком случае получается, что \(F(x+h)-F(x)=\int_{a}^{(x+h)}f(t)dt-\int_{a}^{x}f(t)dt=\int_{a}^{(x+h)} f(t)dt \). Если принять, что \(K=\sup\mid{f}(t), a\leq{t}\leq{b}\), тогда получается следующее выражение: \(\mid{F}(x+h)-F(x)\mid{\leq}\mid\int_{x}^{(x+h)}f(t)dt\mid\leq{K}\mid{h}\mid\rightarrow{0},h\rightarrow0. \)

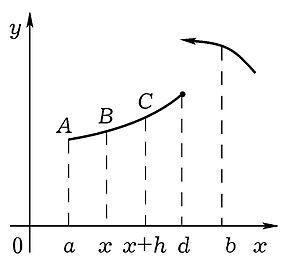
Посмотрите на рисунок: 

Источник: ru.wikipedia.org

На данном рисунке вы можете видеть графическое изображение f. Площадь изменяемой фигуры aABx будет эквивалентна F(x). Если увеличить функцию на \(F(x+h)-F(x)\), то конечная величина будет эквивалентна площади формы \(xBC(x+h)\). Абсолютно понятно, что она будет из-за лимитированности f будет бесконечно желать уйти в абсолютный ноль в случае \(h\rightarrow0\). Причем такой исход не зависит от того, примет ли x вид непрерывной точки или разорвется ли f посредством точки \(x-d\). 

Представим,что функция f становится и интегрируемой в сегменте [a, x], и не прерывается в месте, где \(x\in{[a,x]}\). Нужно доказать, что в таком случае F будет обладать в этом месте производной, что эквивалентна \(F^{\prime}(x)=f(x)\). 

В реальности в месте x, которое указано на отрезке, будет такое выражение: \(\frac{F(x+h)-F(x)}{h}=\frac{1}{h}\int_{x}^{(x+h)}f(t)dt=\frac{1}{h}\int_{x}^{(x+h)}(f(x)+\eta(t))dt=\frac{1}{h}\int_{x}^{(x+h)}f(x)dt+\frac{1}{h}\int_{x}^{(x+h)}\eta(t)dt=f(x)+0,h\rightarrow0.\)

Располагаем \(f(t)=f(x)+\eta({t})\). Из-за того что f(x) не изменяется в отношении t, тогда \(\int_{z}^{(z+h)}f(x)dt=f(x)h \). Потом, из-за того что f не прерывается в точке x для всех \(\epsilon>0\), возможно представить такого вида \(\delta\), при котором \(\mid\eta(t)\mid<\epsilon\) в случае \(\mid{x-t}<\delta\). 

Из-за этого \(\mid\frac{1}{h}\int_{x}^{(x+h)}\eta(t)dt\mid\leq\frac{1}{\mid{h}\mid}\mid{h}\mid\epsilon=\epsilon, \mid{h}\mid<\delta\). Это выражение является доказательством того, что в левой стороне данного выражения существует \(F(a)=\int_{a}^{a}f(t)dt=0 \) при условии, что \(h\rightarrow{0}\). 

Движение к пределу в \(\frac{F(x+h)-F(x)}{h}=\frac{1}{h}\int_{x}^{(x+h)}f(t)dt=\frac{1}{h}\int_{x}^{(x+h)}(f(x)+\eta(t))dt=\frac{1}{h}\int_{x}^{(x+h)}f(x)dt+\frac{1}{h}\int_{x}^{(x+h)}\eta(t)dt=f(x)+0,h\rightarrow0\) указывает на то, что есть производная от F в месте x. Тогда выражение \(F^{\prime}(x)=f(x)\) является абсолютно справедливым. В случае x=a,b будет развиваться единство производной с левой и с правой стороны. 

У данной функции есть производная, которая будет эквивалентна \(f(x)\div{F^{\prime}}(x)=f(x), a\leq{x}\leq{b}\). Получается, что функция F(x) считается первообразной в случае f в сегменте [a, b]. Данное умозаключение нередко именуется в качестве теории интеграла, у которого наблюдается изменяемый верхний предел. Также данная теорема именуется теоремой Барроу. 

Нами было доказано, что не прерываемая произвольная в сегменте [a, b] f-функция обладает в данном сегменте первообразной, которая эквивалентна \(F(x)=\int_{a}^{x}f(t)dt \). Так нами было доказано, что первообразная может иметься у всех функций, которые не прерываются на определенном отрезке. 

Представим, что Ф будет случайной первообразной у функции f(x) в сегменте [a, b]. Существует понимание того, что Ф(x)=F(x)+C. В данной формуле C будет неопределенной произвольной постоянной. При этом будет предполагаться, что x=a. С учетом того, что F(a)=0, то Ф(a) будет равняться C. 

Получается, что \(F(x)=Ф(x)-Ф(a)\). Однако нужно взять во внимание, что \(\int_{a}^{b} f(x)dt=F(b)\). Именно из-за этого \(\int_{a}^{b} f(x)dx=Ф(b)-Ф(a)=Ф(x)\mid_{x=a}^{x=b}\).

Но стоит сказать о том, что в реальности условие того, чтобы подынтегральная функция не прерывалась, лишняя и даже чрезмерная. Для того чтобы данная формула была верна и работала на практике, необходимо, чтобы существовала сторона левая и сторона правая данной формулы. В случае, когда функция f(x) обладает характеристикой интегрируемости, у нее есть первообразная в сегменте [a, b], тогда Ф(x) является абсолютно любой первообразной в данном сегменте. И в таком случае будет справедливо это выражение: \(\int_{a}^{b}f(x)dx=Ф(b)-Ф(a)=Ф(x)\mid_{a}^b\). 

Конечно в практике встречаются функции, которые являются по своей сути интегрируемыми, но не обладают никакой первообразным. Это такие функции, как функция Римана и все функции, у которых есть конечное значение разрывных точек. Также существуют функции, которые не обладают интегрируемостью, но при этом у них есть первообразная (производная \(x^{2}\sin\frac{1}{x^{2}}\), которая имеет дополнение в виде нуля в нуле на всех сегментах, в которых есть ноль. Также их можно наблюдать в случае функций Вольтерры. 

Можно формулу обобщить, если наблюдается ситуация, когда функция обладает итоговым количеством разрывов. Для того чтобы сделать обобщение формулы, необходимо сделать обобщение первообразной, точнее самого термина. Представим, что функция f имеет определение в сегменте [a, b]. Вероятное исключение — конечное значение точек. Так, функция F будет именоваться в качестве обобщенной первообразной f в случаях, при которых: 

• не прерывается в сегменте [a, b]; 
• может быть дифференцируемой во всех местах сегмента [a, b], кроме, вероятно, итогового значения точек;
• в абсолютно всех местах, где функция обладает дифференциацией, кроме, вероятно, итогового значения точек, производная равняется f. 

При этом данная расшифровка понятие не нуждается в том, чтобы производная F в абсолютно всех местах дифференциации была эквивалентна f. С подобной дефицией появляется возможность сделать еще больше обобщение формулы Ньютона-Лейбница. 

Представим, что f определяется в сегменте [a; b] во всех местах, кроме, вероятно, итогового значения точек. В случае, когда функция f(x) обладает свойством интегрируемости, у нее есть первообразная в виде обобщения на участке [a, b]. F(x) будет абсолютно каждой первообразной функции в виде обобщения в этом диапазоне. В таком случае получится выражение \(\int_{a}^{b} f(x)dx=F(b)-F(a)=F(x)\mid_{a}^{b}\). 

Представим доказательство данного выражения. Из-за того что функция f обладает свойством интегрируемости, возможно исследовать абсолютно каждую очередность разбивки с помеченными точками. При этом диаметр данных точек будет стараться уйти в ноль. Предел суммарных интегральных значений в данном случае будет эквивалентен интегралу. 

Нужно рассмотреть то, в какой очередности разбивается сегмент [a; b]. Очередность разбивки \({T_{n}}\) будет таковой, что диаметр деления в случае \(\eta\rightarrow{+\infty}\) будет стремиться к нулевым значением. Нужно включить во все разбивки места сегмента [a; b]. В них F не будет иметь дифференциации или же таким свойством не будет обладать производная данной функции, которая не равняется f. Так, нужно дополнительно обозначить с введением всех этих точек разбивки очередность как \(T_n^\prime\). 

Суммарное значение интегралов любого из отмеченных разбиений \(\left(T_n^{\prime},Xi_n\right)\) эквивалентно равной величине. Получается, что у данных суммарных значений будет одинаковый предел. Получается, что: \(\int_{a}^{b} f\left(x\right)dt=\lim_{n \rightarrow +\infty}\sigma\left(f,T_n^\prime,Xi_{n}\right)=F\left(b\right)-F\left(a\right)\).

Данное доказательство очень занимательно с точки зрения того, что в него рамках не применяются характеристики интегралов. Единственное, что используется — дефиниция интеграла. Но доказать теорию Ньютона-Лейбница невозможно в стандартной (изначальной) дефиниции. Для того чтобы вывести доказательство классического варианта, необходимо помимо всего этого доказать, что все функции обладают непрерывностью, интегрируемостью, а также обладают первообразной. 

Позволим сделать небольшую ремарку. Бесконтрольное использование данной формулы в отношении функций, которые не обладают свойством непрерывности, могут стать причиной ошибочных решений. Одним из примеров неверного расчета является такое выражение: \(\int_{-1}^{1} \frac{dx}{x^{2}}=-\frac{1}{x}\mid_-1^1=-1-1=-2\).

Ошибку спровоцировала функция \(-\frac{1}{x}\), которая не считается первообразной (и не имеет обобщения) для функции \(\frac{1}{x^{2}}\) в диапазоне [-1;1] из-за того, что не имеет определение в 0. У функции в данном диапазоне нет никакой первообразной. К тому же, данная функция не обладает к тому же никакими лимитированности в близости к нулю. А это ведет к тому, что она не имеет интеграции по интегралу Римана.  

Открытие и развитие формулы Ньютона-Лейбница

До того как появился анализ в математике как отдельная дисциплина, эта теорема (на основе геометрии или механики) использовалась шотландским математиком Джеймсом Грегори и английским математиком Исааком Барроу. К примеру, Исаак Барроу дал описание данной формуле еще в 70-х годах 17 века в качестве отношения задач на математические квадратуры, а также на прочерчивание касательной. 

Так выглядел Джеймс Грегори: 

Источник: ru.wikipedia.org

Английский физик Исаак Ньютон создал первую формулировку данной теории при помощи устной формы выражения. Он таким образом представил дефиницию теоремы: чтобы получить нужную величину площади, которая примыкает к какой-то из области абсциссы, данная площадь должна быть всегда взята в качестве результата минусования величин первообразной (которая обозначается условно z), что соответствуют элементам абсцисс, которые лимитируются началом и краем данной площади. 

Так выглядел Исаак Ньютон: 

Источник: ru.wikipedia.org

Немецкий ученый Готфрид Вильгельм Лейбниц сделал на основе словесных указаний собственную формулу. Она обладала иной формой, чем есть сейчас. Но, к сожалению, нигде не сохранилась изначальная форма данной формулы. 

Так выглядел Г.В. Лейбниц: 

Источник: ru.wikipedia.org

Все из-за того, что дефиниция определенного интеграла введена была намного позднее, чем жили Ньютон и Лейбниц. Определение термину дал французский математик Жан-Батист Жозеф Фурье только в 19 веке. Ту форму, которую все используют сейчас, формуле придал французский математик Сильвестр Франсуа де Лакруа в 19 веке. 

Так выглядел Ж. Фурье: 

Источник: ru.wikipedia.org

Важность данной формулы

Базовая теорема оценки создает отношения между вычислениями интеграла и дифференциации. Термин первообразная (и, собственно, термин неопределенный интеграл) можно трактовать при помощи термина производной. Так можно создать отношения соотношения с расчетами дифференциации. Если смотреть с иной стороны, то термин определенный интеграл у Римана превращается в предел. И именно к этому пределу сводят суммарные значения интегралов. 

Интеграл Анри Лебега

Данный интеграл был введен французским математиком Анри Леоном Лебегом. Ученый дал обобщение интегралу Римана на большое число функций. 

Функция \(F\left(x\right):=C+\int_{a}^{x}f\left(t\right)dt \) является по своей сути неопределенным интегралом суммарного значения функции \(f\left(x\right)\). У функции \(F\left(x\right)\) наблюдается абсолютная непрерывность. 

Так выглядит теорема Лебега по своей сути: \(f\left(x\right)\) не имеет никаких разрывов в диапазоне [a,b] в таких случаях, когда есть суммированного функция в сегменте [a,b] под условным названием g. И эта функция: \(f\left(x\right)=f\left(a\right)+\int_{a}^{x}g\left(t\right)dt \) в любой величине x от промежутка a до промежутка b. Следствием данной теоремы является тот факт, что в случае непрерывности функции f в сегменте [a,b], производная данной функции будет находиться в любом месте, она будет суммироваться и будет эквивалентна выражению: \(f\left(x\right)=f\left(a\right)+\int_{a}^{x}f^{\prime}\left(t\right)dt \), в которой \(x\in\left[a,b\right]\). 

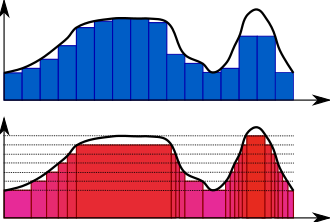
Сравнение интегралов Римана и Лебега (Лебега снизу): 

Источник: ru.wikipedia.org

Иные следствия формулы Ньютона-Лейбница

Одним из вероятных следствий теоремы Ньютона-Лейбница возможно считать формулу подмены переменных и теорию о разложении функций монотонности согласно Анри Лебегу. 

Интеграция частями 

Представим, что f и g являются функциями, которые абсолютно никак не прерываются в сегменте \(\left[a,b\right]\). Получается \(\int_{a}^{b} f^{\prime}\left(x\right)g\left(x\right)dx=f\left(b\right)g\left(b\right)-f\left(a\right)g\left(a\right)-\int_{a}^{b} f\left(x\right)g^{\prime}\left(x\right)dx\)

Данная формула является неизменным следствием из базовой теоремы математического анализа и базового правила Лейбница.