Постройка полигона и гистограммы частот

Что такое полигон и гистограмма частот

Для наглядного представления ряда распределения используют полигон и гистограмму частот.

Существует также полигон относительных частот, представляющий собой ломаную, которая образуется при соединении точек (x₁, W₁), (x₂, W₂),..., (x_k, W_k). Величина W является отношением частоты данного варианта к объему выборочной совокупности и имеет вид:

\(W_i=\frac{n_i}n\)

где n – это объем выборки.

Гистограмму используют в случае непрерывного признака.

Для гистограммы относительных частот основанием прямоугольников ступенчатой фигуры служат частичные интервалы длины h, а высотами – отношение W_i/h.

Как построить полигон частот

Полигон частот строится следующим образом. На оси абсцисс отмечают наблюдения значения x, на оси ординат откладывают соответствующие x_i частоты n_i. Точки с координатами (x_i, n_i), соединенные прямыми отрезками, составляют ломаную – полигон частот.

Пример

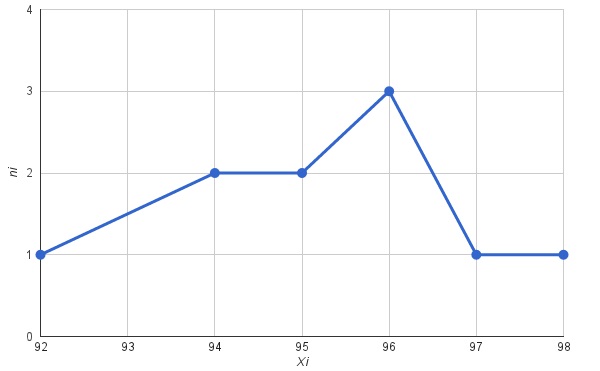
Полигон частот для выборки со следующими значениями:

x_i 92, 94, 95, 96, 97, 98.

n_i 1, 2, 2, 3, 1, 1.

Как построить гистограмму частот

Алгоритм построения гистограммы частот такой: на оси OX отмечаются частичные интервалы h, затем над отложенными значениями проводятся отрезки, параллельные оси OY, на расстоянии отношения плотности частоты n_i/h.

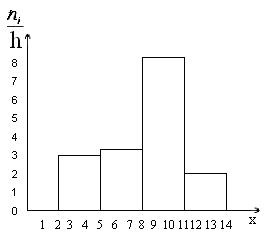
Пример гистограммы частот при частичном интервале h, равном 3.

Сумма частот вариант h: 2–5, 5–8, 8–11, 11–14.

Плотность частоты n_i/h: 3,3; 8,3.

Чему равна площадь гистограммы частот

Площадь отдельного прямоугольника гистограммы равна сумме частот интервала i и имеет вид:

\(\frac{n_ih}h=n_i\)

Площадь всей гистограммы складывается из всех частот, значит, она равна объему выборки.

Примеры создания полигона и гистограммы в задачах

Задача 1

Успеваемость студентов по дисциплине «Высшая математика» представлена в виде баллов:

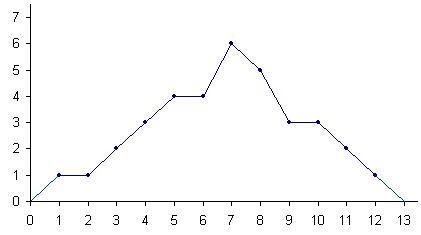
Баллы, x: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.

Количество студентов, n: 1, 1, 2, 3, 4, 4, 6, 5, 3, 3, 2, 1.

Нужно построить полигон частот по этим данным.

Решение

На основе представленной информации строим точки и соединяем их отрезками прямой. Следует заметить, что точки с координатами (0; 0) и (13; 0), которые располагаются на оси OX, имеют своими абсциссами числа на 1 меньшее и большее, чем абсциссы наиболее левой и наиболее правой точек соответственно. Полигон частот выглядит так:

Задача 2

По итогам контрольной работы по биологии среди учеников 9-го класса получена информация о доступности вопросов тестирования (отношение количества учеников, верно ответивших на вопросы, к общему числу учащихся, написавших данную работу). Результаты:

Доступность вопросов, x (%): 25–35, 35–45, 45–55, 55–65, 75–85, 85–95.

Количество вопросов, n: 1, 1, 5, 7, 7, 3, 1.

Всего в контрольной работе было 25 вопросов.

Необходимо построить гистограмму по этому ряду распределения.

Решение

Отмечаем на оси абсцисс 7 отрезков длиной 10. Эти отрезки будут основанием прямоугольников с высотами 1, 1, 5, 7, 7, 3, 1. Ступенчатая фигура, полученная в результате перечисленных действий, является искомой гистограммой.