Гистограмма относительных частот
Что такое полигон относительных частот
Схематическое изображение статистического ряда распределения может быть представлено полигоном и гистограммой частот. Также выделяют понятия полигон относительных частот и гистограмма относительных частот
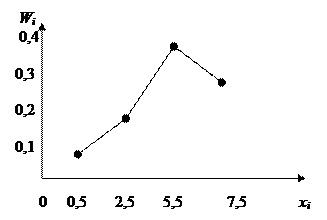
Полигон относительных частот – это ломаная, состоящая из отрезков, соединяющих точки с координатами (xi, ωi).
Построение полигона частот
Алгоритм составления полигона относительных частот: на оси OX отмечают варианты xi, на оси OY откладывают значения ωi. Затем точки с координатами (xi, ωi) соединяют прямыми отрезками. Ломаная, образованная в результате, является полигоном относительных частот.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Пример
Полигон частот для ряда распределения:
xi: 1,5; 3,5; 5,5; 7,5.
ωi: 0,1; 0,2; 0,4; 0,3.
Гистограмма относительных частот, описание
Гистограмма относительных частот – это фигура ступенчатого вида, в составе которой имеются прямоугольники. Основанием этих прямоугольников являются частичные интервалы длиною h, а высотами служит плотность относительной частоты – величина, определяемая с помощью отношения ωi/h.
Строить гистограмму следует, соблюдая следующий порядок. На оси абсцисс указывают частичные интервалы. Над ними на расстоянии, равном плотности относительной частоты (ωi/h), отмечают отрезки, параллельные оси OX.
Пример
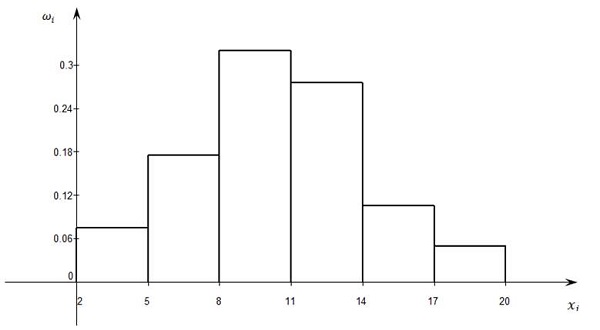
Интервалы, xi: 2–5, 5–8, 8–11, 11–14, 14–17, 17–20.
Частота вариант, ni: 15, 35, 64, 55, 21, 10 (всего 200).
Относительные частоты, ωi: 0,075; 0,175; 0,320; 0,275; 0,105; 0,050 (всего 1,000).
Гистограмма данного ряда распределения имеет вид:
Площадь прямоугольников гистограммы
Площадь одного прямоугольника, входящего в состав гистограммы относительных частот, равна относительной частоте вариант и вычисляется по формуле:
\(h\frac{\omega_i}h=\omega_i\)
Для вычисления площади всей гистограммы необходимо сложить площади всех прямоугольников, составляющих ступенчатую фигуру. Следовательно, искомая величина будет равна единице.
Примеры решения задач
Задача 1
Постройте полигон относительных частот для следующего вариационного ряда:
xi: 2, 7, 8, 15, 16, 17.
ni: 15, 35, 64, 55, 21, 10.
Решение
Для начала необходимо вычислить относительные частоты:
xi: 2, 7, 8, 15, 16, 17.
ni: 15, 35, 64, 55, 21, 10 (итого 200).
ωi: 0,075; 0,175; 0,320; 0,275; 0,105; 0,050 (итого 1,000).
Построим искомую ломаную:
Задача 2
Построить гистограмму относительных частот распределения, имея следующие данные:
Частичный интервал при длине h, равной 3: 2–5, 5–8, 8–11, 11–14.
ni: 9, 10, 25, 6.
Решение
Сначала определим относительные частоты. Для этого установим объем выборочной совокупности n:
n=Σni=50.
Затем найдем ωi:
ω1= 9/50=0,18
ω2= 10/50=0,2
ω3= 25/50=0,5
ω4= 6/50=0,12
Далее вычислим ωi/h, то есть плотность частоты:
0,18/3=0,06
0,2/3=0.07
0,5/3=0,16
0,12/3=0,04
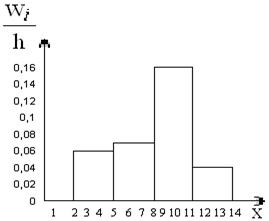
Образуются следующие данные:
Частичный интервал: 2–5, 5–8, 8–11, 11–14.
Сумма относительных частот: 0,18; 0,2; 0,5; 0,12.
Плотность частоты: 0,06; 0,07; 0,16; 0,04.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так