Поток вектора напряженности электростатического поля

Понятие потока вектора напряженности электростатического поля

Полноценно описать электростатическое поле заданной системы зарядов в вакуумной среде можно с помощью эксперимента, подтверждением которого служит закон Кулона, и принципа суперпозиции. При этом есть возможность представить свойства электростатического поля в обобщенном виде без применения утверждения о кулоновском поле точечного заряда. В этом случае целесообразно обратиться к теореме, которая была выведена немецким ученым К. Гауссом, определяющей поток вектора напряженности сквозь произвольную замкнутую поверхность.

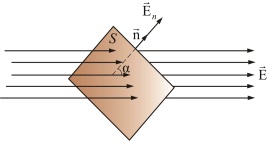
Представим, что через некую площадь S проходят силовые линии однородного электрического поля, напряженность которого равна:

\(\vec{E}\)

Тогда поток напряженности или количество силовых линий, проходящих через площадку, будет рассчитываться по формуле:

\(\Phi _{E}=ES_{\perp }=ES\cos \alpha =E_{n}S\)

Где En является произведением вектора \(\vec{E}\) и нормали \(\vec{n}\)к данной площадке.

Поток вектора напряженности \(\Phi _{E}\) через заданную поверхность представляет собой полное число силовых линий, которые проходят через эту поверхность площадью S.

Формула расчета

Утверждение можно записать в векторной форме. Тогда уравнение будет являться скалярным произведением двух векторов:

\(\Phi _{E}=\left(\vec{E},\vec{S} \right)\)

Где вектор \(\vec{S}\) равен:

\(\vec{S}=\vec{n}S\)

Таким образом, поток вектора \(\vec{E}\) является скалярной величиной, которая в зависимости от угла α может обладать положительным или отрицательным значением. Утверждения можно представить схематично.

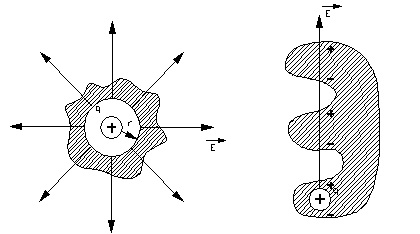
На первом изображении поверхность А1 расположена вокруг положительного заряда, поток направлен наружу, то есть:

\(\Phi _{E}>0\)

Поверхность А2 окружает отрицательный заряд, поток направлен внутрь, то есть:

\(\Phi _{E}<0\)

Общий поток А обладает нулевым значением.

На втором рисунке при условии отличия суммарного заряда внутри поверхности от нуля, поток также не равен нулю. В данной системе поток через поверхность А характеризуется отрицательной величиной. Таким образом, поток вектора напряженности связан с зарядом. В этом заключается смысл теоремы Островского-Гаусса.

Доказательство теоремы Гаусса

Согласно данной закономерности, поток вектора напряженности электростатического поля сквозь произвольную поверхность определяют поток вектора. В единицах измерения СИ \(\Phi _{E}\) = 1 В´м. Вначале необходимо выполнить расчет потока вектора напряженности сквозь сферическую поверхность радиуса r, которая охватывает точечный заряд q, размещенный в ее центральной точке. Формула будет иметь следующий вид:

\(\Phi _{E}=\int_{S}^{}{E_{n}dS}=\frac{kq}{r^{2}}4\pi r^{2}=\frac{q}{\varepsilon _{0}}\)

Уравнение применимо в случае замкнутой поверхности разной формы. Если выделить сферу с помощью произвольной замкнутой поверхности, то каждая линия напряженности, которая пронизывает сферу, будет проходить через эту поверхность. 

Можно представить, что заряд q охватывает какая-то замкнутая поверхность. В случае, когда линии напряженности будут выходить из поверхности, поток станет положительным. Если линии напряженности входят в поверхность, то поток напряженности будет обладать отрицательным значением. Нечетное количество пересечений в процессе расчета потока приводят к одному пересечению.

В виде формулы утверждение можно записать в следующем виде:

\(\Phi _{E}=\int_{S}^{}{\vec{E}d\vec{S}}=\int_{S}^{}{E_{n}dS}=\frac{\sum{q_{i}}}{\varepsilon _{0}}\)

Данную теорему вывел математически для векторного поля любой природы русский математик М.В. Остроградский, а затем независимо от него для электростатического поля — К. Гаусс. В случае, когда заряд не проходит через замкнутую поверхность, то поток будет иметь нулевое значение. Можно представить произвольную поверхность, окруженную N зарядами, тогда

E = SEi

Поток вектора напряженности:

\(\Phi _{E}=\int_{S}^{}{\sum{(\vec{E_{i}}d\vec{S})}}=\sum{\int_{S}^{}{\vec{E_{i}}d\vec{S}}}=\frac{1}{\varepsilon _{0}}\sum{q_{i}}\)

Представленное уравнение демонстрирует поток вектора напряженности через произвольную замкнутую поверхность, которая включает совокупность N зарядов, для электростатического поля в вакуумной среде. Для общего случая характерно распределение электрических зарядов с объемной плотностью r, которая неодинакова в разных точках пространства. В таком случае теорема Гаусса будет иметь следующий вид:

\(\sum{q_{i}}=\int pdV\)

\(\Phi _{E}=\int_{S}^{}{E_{n}dS}=\int_{S}^{}{\vec{E}d\vec{S}}=\frac{1}{\varepsilon _{0}}\int \rho dV\)

Когда поле Е определяется конфигурацией всех зарядов, поток вектора Е через произвольную замкнутую поверхность S зависит от алгебраической суммы зарядов, которые расположены внутри поверхности S. При передвижении зарядов без пересечения поверхности S поток вектора Е сквозь эту поверхность останется прежним.

Применение теоремы Гаусса

Решения формул можно получить с помощью интегрирования уравнения:

\(E=\frac{1}{4\pi \varepsilon _{0}r^{3}}\int_{V}^{}{\rho rdV}\)

Где V является объемом, для которого r не равен нулю.

Но, благодаря использованию теоремы Гаусса, решение задач упрощается. Однако данный метод не всегда можно применить. Он эффективен лишь для ситуаций, когда поле характеризуется специальной симметрией:

• плоской;
• цилиндрической;
• сферической.

Условия применения теоремы Гаусса:

1. Поле обладает специальной симметрией.
2. Наличие достаточно простой замкнутой поверхности, площадь которой можно рассчитать.
3. Возможность преобразования расчета потока в простое произведение напряженности и площади поверхности.

В случае, когда данные условия не выполнимы, расчет Е поля производят другими методами, к примеру, ДИ-дифференцирование и интегрирование. При дискретном распределении зарядов формула будет иметь следующий вид:

\(E=SE_{i}=kS\frac{q_{i}e}{r_{i}^{2}}\)

Применение теоремы Гаусса для расчета напряженности поля равномерно заряженной бесконечной плоскости

Можно представить бесконечную плоскость. Она заряжена с поверхностной плотностью зарядов:

\(\sigma =\frac{dq}{dS}\)

Линии напряженности расположены перпендикулярно относительно плоскости и направлены в обе стороны от плоскости. Поверхность цилиндра можно представить в роли замкнутой поверхности. Основания этой фигуры находятся параллельно по отношению к бесконечной плоскости, а ее ось — перпендикулярна плоскости.

Образующие цилиндрической фигуры расположены параллельно, относительно линий напряженности:

а = 0;

\(\cos a=1\)

Поток вектора напряженности через боковую поверхность равен нулю, а полный поток через цилиндр определяется совокупностью потоков, которые проходят через его основания. Для основания:

\(E_{n}=E\)

Заряд, который заключен внутри постоянной замкнутой поверхности, определяется, как:

\(\sigma S_{osn}\)

Численная характеристика потока равна:

\(\Phi _{E}=E2S_{osn}\)

Согласно теореме Гаусса:

\(\Phi _{E}=\frac{q}{e_{0}}=\frac{\sigma S_{osn}}{e_{0}}\)

Исходя из данного уравнения, следует:

\(E=\frac{q}{2\varepsilon _{0}}S_{osn}=\frac{\sigma }{2\varepsilon _{0}}\)

Напряжение электростатического поля, которое образовано с помощью равномерно заряженной бесконечной плоскости, составляет:

\(E=\frac{S}{2\varepsilon _{0}}\)

В этом случае напряжение электростатического поля не определяется длиной цилиндра. При любом расстоянии от плоскости напряжение будет одинаково по модулю. Поле равномерно заряженной плоскости отличается однородностью.

Применение теоремы Гаусса для расчета напряженности поля двух разноименно заряженных плоскостей, которые бесконечно параллельны друг относительно друга

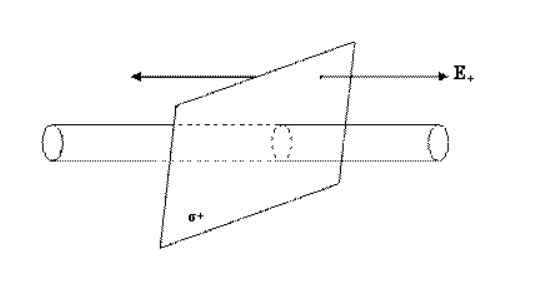
Схематичное представление таких плоскостей представлено на рисунке. Можно представить, что левая плоскость заряжена e + s, а правая с – s. 

Суммарное поле можно рассчитать с помощью определения суперпозиции полей, каждую из которых создают плоскости:

\(E_{I}=E_{III}=0\)

\(E_{II}=E_{+}+E_{-}=\frac{\sigma }{\varepsilon _{0}}\)

\(E=\frac{S }{\varepsilon _{0}}\)

Таким образом, определяется результирующая напряженность поля в области, отделяющей две плоскости. За пределами рассматриваемого объема, который ограничен этими плоскостями, результирующая напряженность поля будет равна нулю.

Применение теоремы Гаусса для расчета напряженности поля равномерно заряженной сферической поверхности

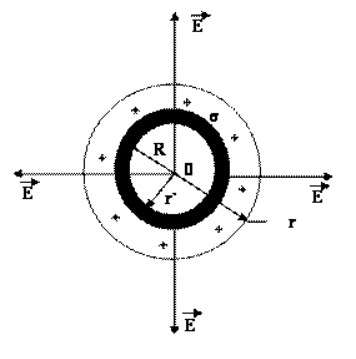
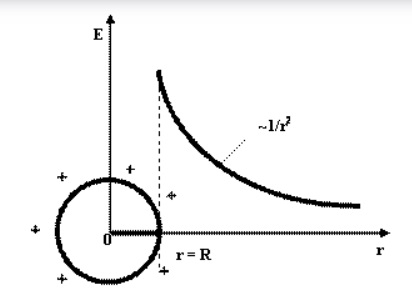
Можно представить сферу, которая равномерно заряжена и обладает радиусом R. Поверхностная плотность заряда равна +s. Для данного поля характерна сферическая симметрия и радиальное направление линий напряженности. Мысленно можно выделить сферу, радиус которой равен r, а центр совпадает с центральной точкой заряженной сферы. Предположим, что r>R. В этом случае справедлива формула:

\(E=\frac{\sigma R^{2}}{\varepsilon _{0}r^{2}}\)

Если r<R, то внутри замкнутой поверхности заряды и электростатическое поле отсутствуют, то есть E =  0. 

Рисунок демонстрирует график зависимости E = f (r)

Пример расчета напряженности поля объемно заряженного шара

Допустим, что шарообразный объект обладает радиусом R. Шар равномерно заряжен, а объемная плотность заряда составляет:

\(r=\frac{dq}{dV}\)

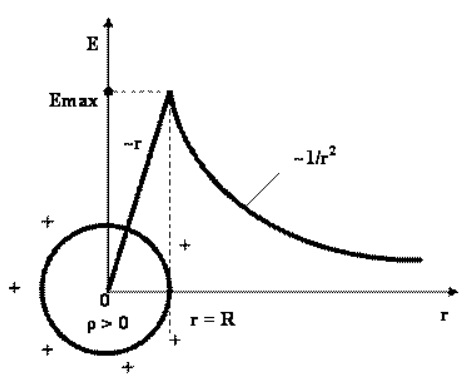
Для данного поля характерна сферическая симметрия. Можно представить сферу замкнутой поверхностью. Когда r>R,

\(E=\frac{q}{4\rho \varepsilon _{0}r^{2}}=\frac{q}{4\rho \varepsilon _{0}R^{2}}\)

В случае, когда r<R, сфера охватывает заряд, который рассчитывается по формуле:

\(q_{c}=q\left( \frac{r_{c}}{R}\right)^{3}\)

Данное уравнение справедливо, так как заряды относятся, как объемы, а объемы, как кубы радиусов. В таком случае, исходя из теоремы Гаусса, следует уравнение:

\(Er=k\frac{qr^{3}}{R^{3}r^{2}}=k\frac{qr}{R^{3}}=\frac{qr}{4\pi \varepsilon _{0}R^{3}}\)

r < R

График демонстрирует зависимость E = f (r)

Внутри шара, который заряжен равномерно, напряженность увеличивается линейно с расстоянием r от его центра. Вне шара напряженность будет уменьшаться обратно пропорционально r2.

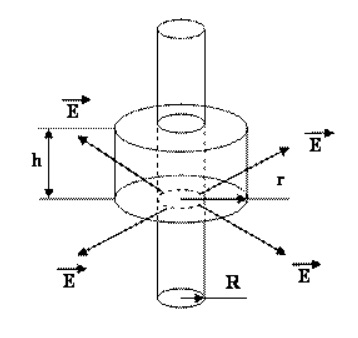
Пример расчета напряженности поля бесконечного круглого цилиндра, который заряжен и обладает линейной плотностью заряда I

Имеется объект цилиндрической формы с радиусом R. Линии напряженности обладают одинаковой густотой и направлены вдоль радиусов круговых сечений цилиндра. Замкнутая поверхность будет представлена в виде цилиндра, радиус которого равен r, а высота — h. Поток вектора через торцы фигуры обладает нулевым значением, а через боковые поверхности составляет:

\(S_{bok}=2\rho rh\)

Следует учитывать, что:

\(E=\frac{Ih}{\varepsilon _{0}}\)

В таком случае:

\(E=\frac{\lambda h}{2\pi \varepsilon _{0}rh}=\frac{\lambda}{2\pi \varepsilon _{0}r}\)

r > R 

В случае, когда l > 0, получаем E > 0, то есть вектор Е будет ориентирован от цилиндра. Если l < 0, то E < 0. В таком случае вектор Е характеризуется направлением к заряженному цилиндру. При r < R, заряды внутри замкнутой поверхности не наблюдаются, следовательно, для этой области E = 0. Поле будет отсутствовать внутри поверхности круглого бесконечного цилиндра, которая равномерна заряжена.