Формулировка принципа Гюйгенса-Френеля

Описание принципа Гюйгенса

Что объясняет

В 1678 году Христиан Гюйгенс предположил, что каждая точка поверхности, куда добирается волна света, становится вторичным источником, отражающим волну. Это объясняло поведение световых волн в прозрачных средах и при контакте с зеркальными поверхностями, но не соответствовало принятой научным сообществом на тот момент корпускулярной теории света.

Основная проблема принципа

Принципа Гюйгенса недостаточно для полного объяснения такого явления, как дифракция. Интерференция в принципе Гюйгенса не учитывалась вовсе.

Работа Френеля над принципом Гюйгенса

Что он изменил и добавил

Большинство маститых учёных — и среди них Жан Био, Пьер Лаплас, Симеон Пуассон — вслед за Исааком Ньютоном считали свет потоком частиц, или корпускул. В рамках корпускулярной теории были сделаны самые значительные открытия в оптике, например, обнаруженная в 1808 году Этьеном Малюсом поляризация света при отражении.

Волновая теория света не могла объяснить поляризацию и двойное лучепреломление, в то время как у её противников имелись на этот счет хоть и громоздкие, но все же вполне приемлемые гипотезы. В 1815 году Огюстен Френель сопоставил волновую и корпускулярную теории света и, признав преимущества корпускулярной в объяснении прямолинейного распространения света, доказал, что те же явления можно объяснить и в рамках гипотезы колебаний. Через некоторое время, исследуя явления поляризации, Френель понял, что их можно объяснить, только приняв предположение о поперечном характере световых волн. Теоретические рассуждения Гюйгенса о том, как волны огибают препятствия, Френель заменил доказательством интерференции вторичных волн.

Формулировка

Дополнение Френеля к принципу Гюйгенса доказывает, что каждый элемент волнового фронта можно считать центром возбуждения вторичных сферических волн. Световое поле в каждой точке пространства будет определяться их интерференцией.

Что объясняет принцип Гюйгенса-Френеля

Независимость волны от источника

Каждая точка поверхности, куда попадает волна, становится вторичным источником волн. Эти волны, попадая в свободное пространство, при движении вперед интерферируют только друг с другом и усиливают друг друга в одинаковых фазах. При движении назад они гасятся при интерференции с первичной, прямой волной. Фазы вторичных волн отличаются от фаз первичных.

Явление дифракции

Если внимательно взглянуть на пятно света, прошедшего через узкое отверстие, можно заметить, что его граница окружена чередующимися тёмными и светлыми полосками. Возникают они за счёт дифракции на краях отверстия.

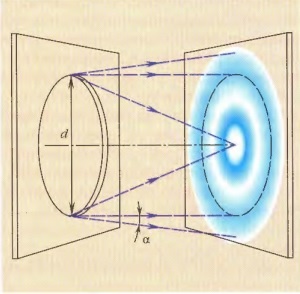
Рассмотрим сечение круглого волнового пучка, выходящего из отверстия диаметром d. Разбив пучок на множество маленьких вторичных источников, проследим, как ведут себя волны, приходящие от любого из них в разные точки пространства. Если выбрать точку наблюдения близко к оси пучка, то вторичные волны в этой точке окажутся в фазе и при сложении будут усиливать друг друга. По мере увеличения расстояния от оси разность фаз между самым близким и самым дальним источниками начнет увеличиваться, и можно обнаружить точку, где волны находятся в противофазе, гасят друг друга.

Чем дальше точка наблюдения от оси пучка, тем больше в нее приходит таких рассогласованных вторичных волн, тем слабее суммарная волна. Точный расчет показывает, что вторичные волны полностью гасят друг друга при распространении под углом к оси пучка. Следовательно, пучок из цилиндрического превращается в конический. Этот угол называют углом дифракции.

При любых условиях дифракции новая, вторичная волна отстает по фазе от первичной на \(\frac{\mathrm\pi}2\).

Несмотря на то, что абсолютно точно описать взаимодействие волн в процессе дифракции можно только в рамках векторной электромагнитной теории, скалярный принцип Гюйгенса-Френеля достаточно адекватно описывает формирование оптического изображения и применяется для решения большинства практических задач. Большая точность необходима лишь для описания работы субдлинноволновых оптических инструментов, а также оптических систем с большой числовой апертурой.

Решение уравнения по принципу

Интегральная формулировка принципа

Формулировка через интеграл по траекториям — это способ найти множество траекторий вторичных волн. Этот способ на основе принципа Гюйгенса-Френеля был адаптирован для расчета бесконечного множества траекторий квантовой амплитуды.

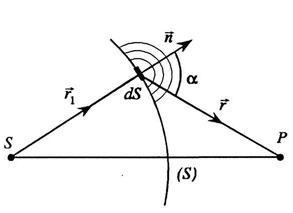
Сущность метода заключается в делении поверхности на столь малые части, чтобы их можно было принять за материальные точки, и последующем суммировании величин по всем участкам изменения конкретной величины. Волновой фронт, расходящийся от точечного источника, имеет вид сферы.

На схеме мы видим точку наблюдения Р, относительно которой определяем комплексную амплитуду поля, обусловленную действием вторичного источника на участке \(ds\), по формуле:

\(K(\alpha)\;\frac{f_0\left(\overrightarrow{r_1}\right)ds}{\lambda r}exp\;(ikr)\)

где \(f_0\left(\overrightarrow{r_1}\right)\) — комплексная амплитуда поля первичной волны на участке ds;

\(K(\alpha)\) — коэффициент наклона;

\(\lambda\) — длина волны.

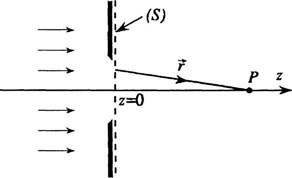
Когда в задаче идет речь о дифракции, нужно применить постулат о граничных условиях и проинтегрировать вышеприведенное выражение по поверхности S, разделяя затененные и не прикрытые экраном участки.

Определение комплексной амплитуды первичной волны в данном случае выглядит следующим образом:

\(\left\{\begin{array}{l}f_0(\xi,\;\eta)\;-\;в\;области\;отверстия\\0\;-\;на\;затененной\;части\end{array}\right.\)

Тогда комплексную амплитуду в точке наблюдения можно найти по формуле:

\(\int\int_sK(\alpha)\;\frac{f\left(s\right)}{\lambda r}exp\;(ikr)ds\)

В оптических задачах часто используется метод зон Френеля. Он позволяет с помощью геометрических построений определить закономерности распределения интенсивности волн. С целью упрощения расчетов волновую поверхность делят на кольцевые зоны.

Примеры решения задач

Задача 1

Вычислить суммарную амплитуду плоской монохроматической дифрагированной волны на щели, плоскость которой перпендикулярна распространению волны, при условии, что экран расположен далеко от щели.

Решение

Так как экран далеко, можно считать, что для участка щели с координатой у расстояние до точки наблюдения равно \(у\;\times\;\sin\left(\psi\right).\)

Если мысленно разбить щель на одинаковые участки шириной \(dy\), одинаковые по модулю комплексные амплитуды от соседних участков в точке наблюдения будут развернуты друг относительно друга на одинаковые углы \(\frac{2\mathrm\pi}\lambda\;\times\;dу\;\times\;\sin\left(\psi\right)\).

Изменение угла psi между нормалью к плоскости щели и направлением наблюдения приведет к изменению угла d\varphi между векторами комплексных амплитуд волн, пришедших от соседних участков щели.

Чтобы найти суммарную амплитуду, нужно сложить комплексные числа с одинаковыми амплитудами и разными фазами \(\frac{2\mathrm\pi}\lambda\;\times\;у\;\times\;\sin\left(\psi\right).\)

Ответ: суммарную амплитуду можно вычислить по формуле:

\(E' = \int_{0}^{d} E_{0}\times exp [i\times\frac{2\pi y}{\lambda}\times\sin\psi]\times dy\)

Задача 2

Квадратное отверстие со стороной 0,2 см освещено параллельным пучком нормально падающих лучей света.

Найти размер изображения отверстия на экране, параллельном отверстию и удаленном от него на 50 метров. За границу изображения на экране принять положение дифракционного максимума первого порядка для наиболее отклоняемых лучей (видимый спектр от 400 до 700 нм).

Решение

Напряженность электрического поля волны в данных условиях можно вычислить с помощью формулы:

\(E(х,у)=\frac{Е_{0}}{b^{2}}\int_{-\frac{b}{2}}^{\frac{b}{2}} exp(-\frac{ikxx'}{l})dx'\int_{-\frac{b}{2}}^{\frac{b}{2}} exp(-\frac{ikyy'}{l})dy'\)

Введем углы дифракции \(\vartheta_1\) и \(\vartheta_2\):

\(\tan\left(\vartheta_1\right)\;=\;\frac хl\)

\(\tan\left(\vartheta_2\right)\;=\;\frac yl\)

Так как расстояние l достаточно велико, углы дифракции малы, соответственно, есть основания предполагать, что их тангенс примерно равен синусу. Тогда формула напряженности поля с подставленными значениями будет выглядеть так:

\(E(х,у)=\frac{Е_{0}}{b^{2}}\int_{-\frac{b}{2}}^{\frac{b}{2}} exp(-ikx'\sin\vartheta_1)dx'\int_{-\frac{b}{2}}^{\frac{b}{2}} exp(-iky'\sin\vartheta_2)dy'\)

Интегрировав выражение, получим:

\(E=Е_0sinc\left(\frac{kb\sin\left(\vartheta_1\right)}2\right)sinc\left(\frac{kb\sin\left(\vartheta_2\right)}2\right)\)

Угловое выражение дифракционных максимумов первого порядка:

\(\frac{kb\sin\left(\vartheta\right)}2\;=\;\frac{3\mathrm\pi}2\)

\(\sin\left(\vartheta\right)\;=\;\frac{3\mathrm\lambda}{2b}\)

Вычислим линейное расстояние D между оптической осью системы и дифракционным максимумом:

\(D\;=\;l\sin\left(\vartheta\right)\;=\;\frac{3\mathrm{λl}}{2b}\)

Подставим в выражение максимальную длину волны видимого света, 700 нм.

Ответ: длина стороны квадрата на экране \(2D\;\approx\;5\;см.\)