Теорема Лейбница для знакочередующихся и знакопеременных рядов

Признак Лейбница для рядов

Знаки элементов такого ряда строго чередуются:

\(\sum\limits_{n=1}^{\infty}(-1)^{n+1}u_n=u_1-u_2+u_3-u_4+u_5-u_6+u_7-u_8+\ldots\)

К примеру, знакочередующимся рядом является

\(1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\ldots\)

В данном случае можно отметить строгое чередование знаков, которое начинается не с первого члена. Для анализа сходимости такого ряда подобное условие является несущественным.

Предположим, что имеется некий знакопеременный ряд:

\(\sum\limits_{n=1}^{\infty}u_n\)

В том случае, когда сходится ряд

\(\sum\limits_{n=1}^{\infty}|u_n|\)

будет сходиться и такой ряд:

\(\sum\limits_{n=1}^{\infty}u_n\)

В данном случае можно заключить, что ряд

\(\sum\limits_{n=1}^{\infty}u_n\)

сходится абсолютно.

В ситуации, когда ряд

\(\sum\limits_{n=1}^{\infty}u_n\)

сходится, но ряд:

\(\sum\limits_{n=1}^{\infty}|u_n|\)

расходится, делают вывод, что ряд

\(\sum\limits_{n=1}^{\infty}u_n\)

сходится условно.

В ситуации, при которой ряд, состоящий из модулей

\(\sum\limits_{n=1}^{\infty}|u_n|\)

расходится, то есть ряд

\(\sum\limits_{n=1}^{\infty}u_n\)

не имеет абсолютной сходимости, требуется воспользоваться дополнительными свойствами. В их числе признак Лейбница.

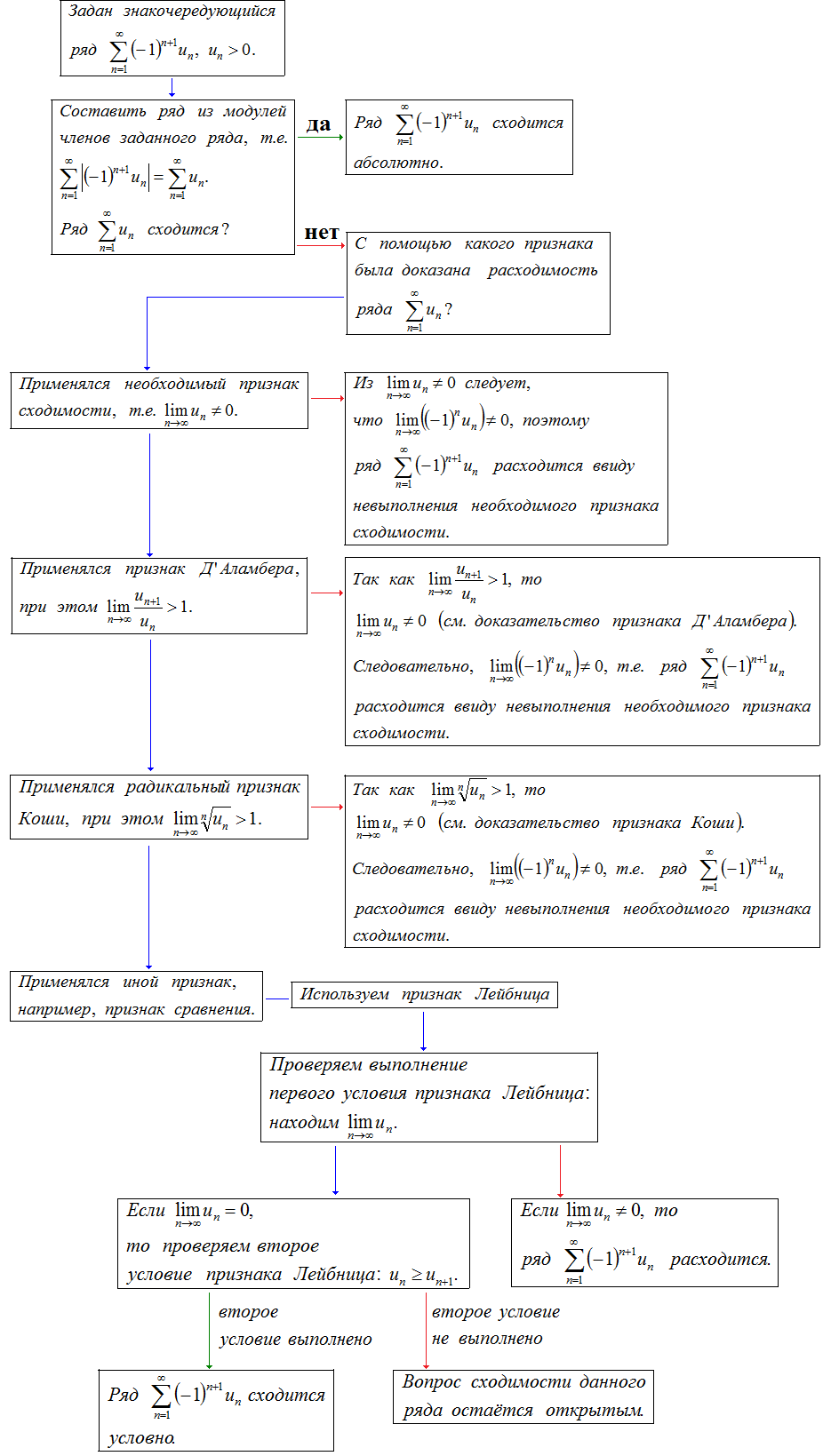
Как исследовать знакочередующийся ряд на сходимость

При решении типовых задач можно встретить знакочередующиеся ряды. С помощью схемы в виде функционального алгоритма, представленной ниже, достаточно просто проанализировать сходимость стандартных знакочередующихся рядов.

Признаки сходимости знакопеременных рядов

Предположим, что существует некий знакочередующийся ряд:

\(\sum\limits_{n=1}^{\infty}(-1)^{n+1}u_n, u_n>0\)

При этом действует пара условий:

\(\lim_{n\to{\infty}}u_n=0\)

\(u_n≥u_{n+1}, n\in{N}\)

Когда оба этих условия справедливы, ряд

\(\sum\limits_{n=1}^{\infty}(-1)^{n+1}u_n\)

сходится.

Второе условия признака Лейбница не во всех случаях реализуется, начиная с первого элемента ряда. Распространены ситуации, при которых элементы \(u_n\) убывают, начиная с какого-то номера \(n_0\in{N}\), не обязательно равного единице. При этом допустимо применять признак Лейбница. Фактически, второе условие признака Лейбница приемлемо сформулировать, как: существует номер \(n_0\in{N}\) такой, что \(u_n≥u_{n+1}\) при всех \(n≥n_0.\)

Признак Лейбница представляет собой достаточное условие, но не является необходимым для сходимости знакочередующихся рядов. Таким образом, если условия выполняются, то ряд гарантированно сходится. Однако при невыполнении этих требований нельзя установить сходимость ряда.

В том случае, когда первое условие признака Лейбница не выполняется, например:

\(\lim_{n\to{\infty}}u_n\neq{0}\)

можно сделать вывод о расходимости ряда:

\(\sum\limits_{n=n_0}^{\infty}(-1)^{n+1}u_n\)

Второе условие может не выполняться как при ситуации схождения, так и в случае расхождения ряда.

Примеры применения теоремы Лейбница

Задача 1

Необходимо определить сходимость ряда:

\(\sum\limits_{n=1}^{\infty}(-1)^{n+1}\frac{4n-1}{n^2+3n}\)

Решение

В первую очередь требуется определить, является ли рассматриваемый ряд знакочередующимся. При n≥1:

\(4n-1≥3>0\)

\(n^2+3n≥4>0\)

Таким образом, при всех \(n\in{N}\) получим:

\(\frac{4n-1}{n^2+3n}>0\)

Можно заключить, что рассматриваемый ряд имеет вид:

\(\sum\limits_{n=1}^{\infty}(-1)^{n+1}u_n\)

где \(u_n=\frac{4n-1}{n^2+3n}>0\)

Заданный ряд является знакочередующимся.

Такую проверку допускается выполнять устно, но пренебречь ей вовсе нельзя. В том случае, когда знаки элементов ряда чередуются не с первого члена, можно исключить «лишние» компоненты ряда и исследовать на сходимость преобразованный ряд.

Следует записать ряд, который включает модули членов данного ряда:

\(\sum\limits_{n=1}^{\infty}\left|(-1)^{n+1}\frac{4n-1}{n^2+3n}\right| =\sum\limits_{n=1}^{\infty}\frac{4n-1}{n^2+3n}\)

В процессе проверки сходимости записанного ряда из модулей следует воспользоваться признаком сравнения. При всех \(n\in{N}\):

\(4n-1=3n+n-1≥3n\)

\(n^2+3n≤n^2+3n^2=4n^2\)

Таким образом:

\(\frac{4n-1}{n^2+3n}≥ \frac{3n}{4n^2}=\frac{3}{4}\cdot\frac{1}{n}\)

Можно заметить расходимость гармонического ряда:

\(\sum\limits_{n=1}^{\infty}\frac{1}{n}\)

По этой причине расходится ряд:

\(\sum\limits_{n=1}^{\infty}\left(\frac{3}{4}\cdot\frac{1}{n}\right)\)

Исходя из признака сравнения, можно сделать вывод о расхождении ряда:

\(\sum\limits_{n=1}^{\infty}\frac{4n-1}{n^2+3n}\)

Далее следует ввести обозначение:

\(u_n=\frac{4n-1}{n^2+3n}\)

Затем целесообразно выполнить проверку, относительно применимости условий признака Лейбница в случае начального знакочередующегося ряда. Для того чтобы найти \(\lim_{n\to{\infty}}u_n\), необходимо:

\(\lim_{n\to{\infty}}u_n =\lim_{n\to{\infty}}\frac{4n-1}{n^2+3n} =\lim_{n\to{\infty}}\frac{\frac{4}{n}-\frac{1}{n^2}}{1+\frac{3}{n}} =0\)

В результате выполняется первое условие признака Лейбница. Далее требуется определить, выполняется ли неравенство:

\(u_n≥u_{n+1}\)

В распространенных случаях при решении подобных задач принято записывать несколько первых элементов ряда, чтобы прийти к выводу о выполнении неравенства \(u_n≥u_{n+1}\). Подобный способ не является корректным. Наиболее простым методом станет анализ разности и определение ее знака:

\(u_n-u_{n+1}\)

Порядок действий:

\(u_n-u_{n+1} =\frac{4n-1}{n^2+3n}-\frac{4(n+1)-1}{(n+1)^2+3(n+1)} =\frac{4n-1}{n^2+3n}-\frac{4n+3}{n^2+5n+4}=\\ =\frac{(4n-1)\cdot\left(n^2+5n+4\right)-\left(n^2+3n\right)\cdot(4n+3)}{\left(n^2+3n\right)\cdot\left(n^2+5n+4\right)} =\frac{4n^2+2n-4}{\left(n^2+3n\right)\cdot\left(n^2+5n+4\right)}\)

При n≥1:

\(4n^2-4≥0\)

Таким образом:

\(4n^2+2n-4>0\)

\(u_n-u_{n+1}>0, u_n>u_{n+1}\)

В итоге выполняются все условия для признака Лейбница. Можно отметить расхождение ряда:

\(\sum\limits_{n=1}^{\infty}\left|(-1)^{n+1}\frac{4n-1}{n^2+3n}\right|\)

Следовательно, будет сходиться условно ряд:

\(\sum\limits_{n=1}^{\infty}(-1)^{n+1}\frac{4n-1}{n^2+3n}\)

Ответ: ряд сходится условно.

Задача 2

Задан ряд:

\(\sum\limits_{n=1}^{\infty}(-1)^{n+1}\frac{5n-4}{\sqrt{2n^3-1}}\)

Требуется исследовать сходимость этого ряда.

Решение

В первую очередь необходимо проанализировать выражение:

\(\frac{5n-4}{\sqrt{2n^3-1}}\)

Далее следует проверить, насколько корректны условия. Это связано с распространенными ошибками, которые встречаются в задачах и заключаются в том, что подкоренное выражение может быть отрицательным, либо некоторые значения n обращают знаменатель в нуль. При n≥1:

\(2n^3≥2\)

Тогда при \(2n^3-1≥1 \) исключается отрицательное или нулевое выражение под корнем. Таким образом, условия является корректным. При всех n≥1 определено выражение:

\(\frac{5n-4}{\sqrt{2n^3-1}}\)

При n≥1 справедливо неравенство:

\(\frac{5n-4}{\sqrt{2n^3-1}}>0\)

Можно сделать вывод, что заданный ряд является знакочередующимся. Далее следует записать ряд из модулей элементов рассматриваемого ряда:

\(\sum\limits_{n=1}^{\infty}\left|(-1)^{n+1}\frac{5n-4}{\sqrt{2n^3-1}}\right| =\sum\limits_{n=1}^{\infty}\frac{5n-4}{\sqrt{2n^3-1}}\)

С помощью второго признака сравнения или признака сравнения в предельной форме нужно сравнить два ряда:

\(\sum\limits_{n=1}^{\infty}\frac{5n-4}{\sqrt{2n^3-1}}\)

\(\sum\limits_{n=1}^{\infty}\frac{1}{\sqrt{n}}\)

Получим:

\(\lim_{n\to\infty}\frac{\frac{5n-4}{\sqrt{2n^3-1}}}{\frac{1}{\sqrt{n}}} =\lim_{n\to\infty}\frac{5n\sqrt{n}-4\sqrt{n}}{\sqrt{2n^3-1}} =\lim_{n\to\infty}\frac{\frac{5n\sqrt{n}}{n\sqrt{n}}-\frac{4\sqrt{n}}{n\sqrt{n}}}{\sqrt{\frac{2n^3-1}{n^3}}} \lim_{n\to\infty}\frac{5-\frac{4}{n}}{\sqrt{2-\frac{1}{n^3}}} =\frac{5}{\sqrt{2}}\)

При условии, что:

\(\frac{5}{\sqrt{2}}\neq{0} и \frac{5}{\sqrt{2}}\neq\infty\)

ряды будут расходиться:

\(\sum\limits_{n=1}^{\infty}\frac{1}{\sqrt{n}}\)

\(\sum\limits_{n=1}^{\infty}\frac{5n-4}{\sqrt{2n^3-1}}\)

В результате, равномерный знакочередующийся ряд не обладает абсолютной сходимостью. Можно ввести обозначение:

\(u_n=\frac{5n-4}{\sqrt{2n^3-1}}\)

для проверки справедливости условий признака Лейбница. Следует определить \(\lim_{n\to{\infty}}u_n:\)

\(\lim_{n\to{\infty}}u_n =\lim_{n\to{\infty}}\frac{5n-4}{\sqrt{2n^3-1}} =\lim_{n\to{\infty}}\frac{\frac{5n}{n^{\frac{3}{2}}}-\frac{4}{n^{\frac{3}{2}}}}{\sqrt{\frac{2n^3-1}{n^3}}} =\lim_{n\to{\infty}}\frac{\frac{5}{\sqrt{n}}-\frac{4}{n^{\frac{3}{2}}}}{\sqrt{2-\frac{1}{n^3}}} =0\)

Выполнимость первого условия признака Лейбница доказана. Относительно справедливости второго условия, нужно рассмотреть функцию вместо \(u_n=\frac{5n-4}{\sqrt{2n^3-1}}\):

\(y(x)=\frac{5x-4}{\sqrt{2x^3-1}}\)

x≥1

В том случае, когда функция не возрастает и не убывает, \(x_2>x_1\). Получим:

\(y(x_1)≥y(x_2)\)

Предположим, что:

\(x_1=n\)

\(x_2=n+1\)

Из неравенства n+1>n последует справедливость неравенства:

\(y(n)≥y(n+1)\)

При \(y(n)=u_n\) неравенство \(y(n)≥y(n+1)\) соответствует \(u_{n}≥u_{n+1}.\)

При y(x) в виде убывающей функции, из неравенства n+1>n последует истинность неравенства \(y(n)>y(n+1)\), то есть \(u_{n}>u_{n+1}\). Следует определить производную \(y'(x)\) и ее натуральный знак для соответствующих значений х:

\(y'(x)=\frac{(5x-4)'\cdot\sqrt{2x^3-1}-(5x-4)\cdot\left(\sqrt{2x^3-1}\right)'}{\left(\sqrt{2x^3-1}\right)^2} =\frac{5\cdot\sqrt{2x^3-1}-(5x-4)\cdot\frac{1}{2\sqrt{2x^3-1}}\cdot{6x^2}}{2x^3-1}=\\ =\frac{5\cdot\left(2x^3-1\right)-(5x-4)\cdot{3x^2}}{\left(2x^3-1\right)^{\frac{3}{2}}} =\frac{-5x^3+12x^2-5}{\left(2x^3-1\right)^{\frac{3}{2}}}\)

При достаточно больших положительных значениях x≥1 многочлен на месте знаменателя будет меньше нуля:

\(-5x^3+12x^2-5<0\)

Данный вывод можно доказать с помощью лемме о модуле старшего члена. Если |x| обладает достаточно большими значениями, знак многочлена совпадает со знаком его старшего члена. Применяя утверждение к заданным условиям, получим такое число c≥1, при котором для всех x≥c будет верным неравенство:

\(-5x^3+12x^2-5<0\)

Наличие такого числа является достаточным условием для дальнейших расчетов. С другой стороны, можно оценить значение выражения:

\(-5x^3+12x^2-5\)

Так как:

\(-5x^3+12x^2-5=x^2(-5x+12)-5\)

при x≥3:

\(-5x+12<0\)

В результате:

\(x^2(-5x+12)-5<0\)

Можно заключить, что при x≥3 имеем \(y'(x)<0\), то есть функция y(x) убывает. Таким образом, при n≥3 получает доказательство неравенство \(u_n>u_{n+1}\), то есть второе условие признака Лейбница выполнено. Выполнение второго условия не с n=1, а с n=3, является несущественным.

В процессе исследования при выполнении обоих условий признака Лейбница ряд будет расходиться:

\(\sum\limits_{n=1}^{\infty}\left|(-1)^{n+1}\frac{5n-4}{\sqrt{2n^3-1}}\right|\)

Следовательно, условно сходиться будет ряд:

\(\sum\limits_{n=1}^{\infty}(-1)^{n+1}\frac{4n-1}{n^2+3n}\)

Ответ: ряд сходится условно.

Задача 3

Записан ряд:

\(\sum\limits_{n=1}^{\infty}(-1)^{n+1}\frac{3n+4}{2^n}\)

Требуется определить сходимость ряда.

Решение

Знакочередующийся ряд можно составить из модулей его элементов:

\(\sum\limits_{n=1}^{\infty}\left|(-1)^{n+1}\frac{3n+4}{2^n}\right| =\sum\limits_{n=1}^{\infty}\frac{3n+4}{2^n}\)

Целесообразно воспользоваться признаком Д'Аламбера. Введем обозначение:

\(u_n=\frac{3n+4}{2^n}\)

В результате:

\(u_{n+1}=\frac{3n+7}{2^{n+1}}\)

Таким образом:

\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\lim_{n\to\infty}\frac{u_{n+1}}{u_{n}} =\lim_{n\to\infty}\frac{\frac{3n+7}{2^{n+1}}}{\frac{3n+4}{2^n}} =\frac{1}{2}\lim_{n\to\infty}\frac{3n+7}{3n+4} =\frac{1}{2}\lim_{n\to\infty}\frac{3+\frac{7}{n}}{3+\frac{4}{n}} =\frac{1}{2}\cdot{1}=\frac{1}{2}\)

При \(\frac{1}{2}<1\), ряд будет сходиться:

\(\sum\limits_{n=1}^{\infty}\frac{3n+4}{2^n}\)

Сходимость ряда:

\(\sum\limits_{n=1}^{\infty}\left|(-1)^{n+1}\frac{3n+4}{2^n}\right|\)

позволяет сделать вывод о том, что абсолютно сходится ряд:

\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\sum\limits_{n=1}^{\infty}(-1)^{n+1}\frac{3n+4}{2^n}\)

Ответ: ряд сходится абсолютно.