Проводники в электростатическом поле

Что такое проводники в электростатическом поле

В зависимости от электрических характеристик все вещества в физике принято делить на две большие категории — вещества, способные проводить электрический ток, и вещества, которые не проводят электричество. Первая категория носит название проводников, а вторая — диэлектриков или изоляторов.

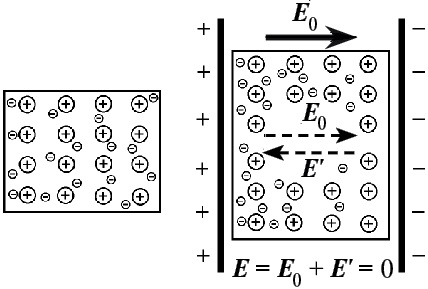
Структура вещества представлена набором атомов, состоящих из зарядов. При отсутствии вокруг вещества внешнего поля, распределение частиц осуществляется таким образом, что сумма внутренних электрических полей имеет нулевое значение. В случае помещения вещества в среду внешнего электрического поля, оно оказывает воздействие на заряды. В результате частицы перераспределяются, что приводит к образованию собственного электрического поля. Полное электрическое поле \(\vec{E}\) представляет собой сумму внешнего поля \(\vec{E_{0}}\) и внутреннего поля \( \vec{E^{'}}\) сформированного с помощью зарядов.

Какие вещества являются проводниками

Проводники проводят электричество. Типичными проводниками принято считать металлы. Важной особенностью проводников является присутствие свободных зарядов, участвующих в тепловом движении и способных двигаться по всему объему вещества.

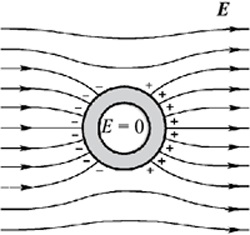
Если внешнее поле отсутствует, в любой области проводника положительные заряды, составляющие ионную решетку, компенсируют отрицательные свободные заряды. В итоге поверхность проводника наполняется нескомпенсированными положительными и отрицательными заряженными частицами. Такое явление носит название электростатической индукции. Образующиеся заряженные частицы на поверхности вещества называют индукционными зарядами. Такие заряженные частицы обладают собственным полем \(\vec{E^{'}}\) компенсирующим внешнее поле \(\vec{E_{0}}\) по всему объему проводника:

\(\vec{E}=\vec{E_{0}}+\vec{E^{'}}=0\)

В чем отличие проводника от диэлектрика

В отличие от диэлектрических веществ, материалы, которые способны проводить электричество, обладают высокой концентрацией свободных носителей заряда. Для металлов характерно присутствие свободных электронов, которые по сравнению со связанными электронами, перемещаются по всему объему вещества.

Образование свободных электронов связано с тем, что атомы металлических веществ обладают валентными электронами, слабо взаимодействующими с ядрами и достаточно просто теряющими связи с ними. Таким образом, металл является кристаллической решеткой, включающей узлы с положительными ионами, которые окружены отрицательным электронным газом.

Вначале наблюдается образование поля с такой же напряженностью \(E_{0}\) внутри проводника. Данное поле будет воздействовать на свободные электроны. В результате заряды приходят в движение в противоположном направлении полю \(E_{0} \). В процессе распределения электронов образуется внутреннее поле $$E_{‘}$$. Его направление будет противоположно внешнему полю $$E_{0}$$. Перемещение электронов прекращается в том случае, когда суммарное поле внутри материала примет нулевое значение:

\(E=E_{0}-E_{‘}=0\)

Данное равенство подтверждено многочисленными практическими опытами. Известно, что с помощью замкнутой проводящей оболочки целиком экранируется находящаяся внутри нее область от внешних электрических полей. Таким образом, образуется электростатическая защита.

Условия равновесного состояния заряда в проводнике

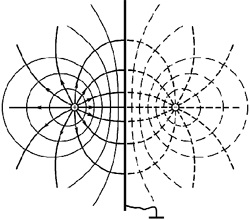
Можно представить пару точечных зарядов, модули которых одинаковы, а знаки противоположны. Такие заряженные частицы +q и –q отдалены друг от друга на некоторое расстояние. Они создают электростатическое поле, в котором наблюдают системы с взаимно перпендикулярными силовыми линиями и эквипотенциальными поверхностями. В качестве одной из таких поверхностей представлена плоскость. Она пролегает сквозь середину отрезка, который соединяет заряженные частицы. Плоскость обладает нулевым потенциалом, так как, исходя из принципа суперпозиции, если точки удалены на равные расстояния r1 = r2 от заряженных частиц, то:

\(\varphi =\varphi _{1}+\varphi _{2}=k\frac{q}{r_{1}}-k\frac{q}{r_{2}}=0\)

Далее необходимо совместить плоскость и тонкую проводящую пластину с последующим ее заземлением.

Можно наблюдать, что поле при этом сохранит стабильность, так как все точки пластины обладают одинаковым потенциалом, равным нулю. При исключении заряда –q, который наблюдается за проводящей пластиной, поле перед ней не изменится. Исходя из этого, можно сделать вывод о том, что при приближении тонкой проводящей заземленной пластины к точечному заряду электрическое поле, которое создают реальный заряд и его мнимое изображение противоположного знака в пластине, будет совпадать с полем в зеркале. Способ электростатических изображений не является универсальным методом, однако с его помощью можно упростить решение многих задач.

Примеры решения задач

Задача №1

Облако небольшого размера обладает зарядом q. Оно располагается на высоте h над землей. Если принять землю за проводник, то необходимо определить, какова напряженность поля, которое создает этот заряд на расстоянии S от точки, над которым расположен заряд. В этом случае кривизна поверхности не учитывается.

Решение

Точечный заряд имеет вид небольшого заряженного облака в данном случае. Для поля точечного заряда характерна сферическая симметрия. На поверхности земли наблюдается образование индуцированных зарядов. Линии напряженности исходят радиально из точечного заряда +q и достигать поверхности земли под прямым углом. В таком случае сторона, которая обращена к положительному заряду, покрывается отрицательными зарядами. На внутренней стороне поверхности земли заряды отсутствуют.

Справедливо утверждение, что отрицательные заряды, приходящие из земли, скомпенсируют положительный заряд, который образовался на внутренней поверхности земли. Результирующее поле будет соответствовать полю двух точечных равных, но разноименных зарядов, удаленных на расстояние 2h друг от друга. Поверхность земли при этом представляет собой эквипотенциальную поверхность. Таким образом:

\(E_{1}=E_{2}\)

Результирующее поле будет рассчитано следующим образом:

\(E(r)=2E_{1}\cos \alpha =\frac{2q}{4\pi \varepsilon _{0}r^{2}}\cos \alpha =\frac{2q}{4\pi \varepsilon _{0}(S^{2}+h^{2})(S^{2}+h^{2})^{\frac{1}{2}}}=\frac{2qh}{4\pi \varepsilon _{0}(S^{2}+h^{2})^{\frac{3}{2}}}\)

Задача №2

Требуется рассчитать поверхностную плотность \(\sigma\) заряда под зарядом.

Решение

Поверхностная плотность заряда представляет собой функцию координат на поверхности земли. Изменения вектора напряженности происходят скачками от E(r) до нулевых значений, так как внутри земли нет электрического поля. Изменения можно рассчитать таким образом:

\(\Delta E=\frac{\sigma }{\varepsilon _{0}}\)

С учетом отсутствия поля в земле уравнение можно записать в виде:

\(\frac{\sigma }{\varepsilon _{0}}=\frac{2qh}{4\pi \varepsilon _{0}(S^{2}+h^{2})^{\frac{3}{2}}}\)

Из данного равенства следует:

\(\sigma=\frac{2qh}{4\pi \varepsilon _{0}(S^{2}+h^{2})^{\frac{3}{2}}}==\frac{2qh}{4\pi r^{3}}\)

с учетом \(r^{2}=S^{2}+h^{2}\)

Под зарядом \(S = 0\), из чего следует:

\(\sigma _{1}=-\frac{2qh}{4\pi h^{3}}=-\frac{q}{2\pi h^{2}}\)

Задача №3

Проводящий предмет обладает зарядом q и располагается внутри замкнутой металлической оболочки. Необходимо выяснить, изменится ли внешнее электрическое поле при перемещении объекта внутри оболочки.

Решение

Как бы ни располагался проводник с зарядом +q  под оболочкой, его внутренняя поверхность будет обладать зарядом –q, распределенным так, что поле в структуре металла отсутствует. Верхняя сторона оболочки будет обладать зарядом +q, распределяемым таким образом, что поле в толще материала будет отсутствовать. Распределение заряда +q по внешней стороне оболочки не зависит от положения, которое занимает проводник внутри оболочки. Из этого можно сделать вывод, что изменения поля вне оболочки отсутствуют во время движения проводника внутри оболочки.

Можно представить, что оболочка обладает сферической формой. В этом случае индуцированный на ее внешней поверхности заряд, который распределен равномерно, сформирует вне оболочки поле, которое не определяется расположением и геометрическими размерами заряженного проводника внутри сферы и обладает сферической симметрией, а напряженность E и потенциал в каждой точке этого поля будут рассчитаны таким образом:

\(E=\frac{1}{4\pi \varepsilon _{0}}\frac{q}{r^{2}}\)

\(\phi =\frac{1}{4\pi \varepsilon _{0}}\frac{q}{r}\)

Где r является расстоянием от центра сферы до рассматриваемой точки.

Задача №4

Однородное электростатическое поле обладает напряженностью Е. В это поле помещают пластину из металла площадью S. Необходимо определить заряд, который будет индуцироваться на сторонах пластины.

Решение

Представим, что правой стороне пластины соответствуют положительно заряженные частицы, а левой — отрицательные. С помощью этих зарядов будет образовано поле с напряженностью, которую можно рассчитать по формуле:

\(E=\frac{\sigma }{2\varepsilon _{0}}+\frac{\sigma }{2\varepsilon _{0}}=\frac{\sigma }{\varepsilon _{0}}\)

Где σ является поверхностной плотностью зарядов.

Определив сумму полей, можно определить результирующее поле:

\(E-\frac{\sigma }{\varepsilon _{0}}\)

Исходя из того, что пластина представляет собой проводник, получаем равенство:

\(E-\frac{\sigma }{\varepsilon _{0}}=0\)

Из этого уравнения получим:

\(\sigma =\varepsilon _{0}E\)

В таком случае искомый заряд будет рассчитан по формуле:

\(q=\sigma S =\varepsilon _{0}ES\)

Задача №5

Пару металлических пластин расположили параллельно. Они отдалены на небольшое расстояние. Первую пластину заряжают положительно, ее заряд составляет q. Необходимо определить заряды, индуцированные на поверхности второй пластины.

Решение

Правая сторона второй пластины будет обладать положительным зарядом, а левая — отрицательным. С помощью этих зарядов будет образовано поле с напряженностью:

\(E=\frac{\sigma }{2\varepsilon _{0}}+\frac{\sigma }{2\varepsilon _{0}}=\frac{\sigma }{\varepsilon _{0}}=\frac{q}{\varepsilon _{0}S}\)

Где q является величиной заряда, который образован на сторонах второй пластины, S представляет собой площадь пластины.

Кроме общего поля на второй пластине будет сформировано поле:

\(E=\frac{q }{2\varepsilon _{0}S}\)

Данное поле формируется с помощью заряда первой пластины. Результирующее поле будет обладать нулевым значением. Таким образом:

\(\frac{q }{2\varepsilon _{0}S}-\frac{ q^{'} }{\varepsilon _{0}S}=0\)

Из этого равенства следует, что:

\(q^{'}=\frac{q}{2}\)