Распределение Больцмана

Что такое распределение Больцмана

Данная закономерность объясняет принцип деления частиц, которые находятся под воздействием силового поля, при условии теплового равновесия. Принцип описан Л. Больцманом в 1868 – 1871 гг.

Исходя из распределения Больцмана, можно рассчитать количество частиц с полной энергией \(E_{i}\) в среднем:

\(\\left =\frac{1}{Z}e^{-\frac{E_{i}}{k_{B}t}}N_{i}\)

где \(N_{i}\) является переменной кратностью состояния частицы с энергией \(E_{i}\) или числом возможных состояний частицы с энергией \(E_{i}\).

Постоянная Z рассчитывается с условием, что сумма \(n_{i}\) со всеми возможными значениями i составляет заданное полное количество частиц n в системе, что является условием применения для нормировки:

\(\sum_{i}^{}{n_{i}}=n\)

При условии, что частицы перемещаются, согласно пояснению принципов классической механики, энергия \(E_{i}\) состоит из следующих компонентов:

1. Кинетическая энергия \(E^{1}_{i}=E_{i}\) (кин) частицы в виде молекулы или атома.
2. Внутренняя энергия \(E^{2}_{i}=E_{i}\) (вн), к примеру, энергия возбуждения электронов.
3. Потенциальная энергия \(E^{2}_{i}=E_{i}\) (пот), характерная для внешнего поля, которая определяется положением частицы в пространстве.

\(E_{i}= E^{1}_{i}+ E^{2}_{i}+ E^{3}_{i}\)

Распределение Больцмана в поле сил тяжести

Можно рассмотреть нахождение идеального газа в поле, в котором действуют консервативные силы, с тепловым равновесием. В зависимости от точек с разными значениями потенциальной энергии определяется концентрация газа, что позволяет соблюсти условия механического равновесия. Количество молекул на единицу объема n уменьшается во время удаления от поверхности Земли, и величина давления убывает, исходя из уравнения:

\(P\;=\;nkT\)

Когда определено количество молекул в единице объема, можно найти и величину давления. Справедлив и обратный принцип выполнения расчета числа молекул в определенном объеме при известном давлении. Плотность среды и параметры давления находятся в пропорциональной зависимости друг от друга, в условиях стабильных температурных показателей. Рост величины давления с уменьшением высоты объясняется тем, что на нижний слой оказывается нагрузка в виде веса всех атомов, которые находятся выше этого уровня.

Согласно основному уравнению молекулярно-кинетической теории можно P заменить на n для барометрической формулы и получить, таким образом, распределение Больцмана для молярной массы газа:

\(n=n_{0}e^{-\frac{\mu gh}{RT}}\)

Где n является количеством молекул в единице объема на высоте h = 0 и h.

Согласно уравнению:

\(\mu =mN_{a}\)

и формуле:

\(R=N_{a}k\)

распределение Больцмана имеет следующий вид:

\(n=n_{0}e^{-\frac{mgh}{kT}}\)

Количество молекул на высоте, не равной нулю, уменьшается при понижении температуры. Если Т = 0, нельзя наблюдать тепловое движение. В этом случае все молекулы были бы распределены на поверхности Земли. Высокая температура, наоборот, способствуют практически равномерному распределению молекул по высоте. При этом показатели плотности молекул медленно уменьшаются с высотой. Исходя из уравнения потенциальной энергии:

\(U = mgh\)

в зависимости от высоты U будет отличаться. Таким образом, равенство:

\(n=n_{0}e^{-\frac{mgh}{kT}}\)

является характеристикой распределения частиц, согласно величине потенциальной энергии:

\(n=n_{0}e^{-\frac{U}{kT}}\)

Данное уравнение является законом распределения частиц, согласно потенциальным энергиям, или распределением Больцмана. В этом случае \(n_{0}\) представляет собой количество молекул на единицу объема там, где U = 0.

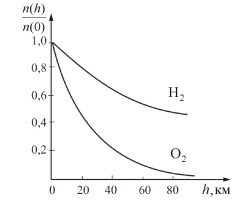
Наглядно продемонстрировать зависимость концентрации разных газообразных веществ от высоты можно с помощью графика. Таким образом, количество более тяжелых молекул во время увеличения высоты уменьшается быстрее, чем легких.

Исходя из выведенной формулы, отношение концентраций молекул в точках с \(U_{1}\) и \(i>U_{2}\) будет записано в таком виде:

\(\frac{n_{1}}{n_{2}}=e^{-\frac{U_{1}-U_{2}}{kT}}\)

Больцманом было доказано, что данная формула справедлива и для потенциального поля с силами гравитации, и для любого потенциального поля с совокупностью каких-либо одинаковых частиц, которые совершают хаотичное тепловое движение.

Барометрическая формула Больцмана, вывод

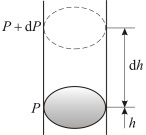
На какой-то высоте h можно наблюдать атмосферное давление, наличие которого объясняется весом слоев газа, находящихся выше этого уровня. Можно представить, что Р является давлением на высоте h, а P + dP характерно для h + dh.

Следует отметить, что dh > 0, а dP < 0, так как для больших высот характерно меньшее давление. Разность давления P – (P + dP) соизмерима с весом газа, который заключен в объеме цилиндра, площадь основания которого составляет единицу, а высота равна dh. Так как:

\(P=\rho gh\)

где \(\rho =\frac{P\mu }{RT}\) является плотностью газа на высоте h, постепенно уменьшающейся с высотой. Согласно этому, можно представить следующее равенство:

\(P-\left(P+dP \right)=\rho gdh\)

Исходя из этого равенства, можно записать барометрическое уравнение, которое будет иметь следующий вид:

\(P=P_{0}e^{-\frac{mgh}{RT}}\)

где \(P_{0}\) является величиной давления на высоте h = 0.

Правила построения графика

Согласно выведенной закономерности, можно заметить, что скорость убывания Р тем больше, чем выше масса газа или больше μ и чем ниже показатели температуры. В качестве практического примера можно рассмотреть концентрацию легких газообразных веществ таких, как Н_е и Н₂, которая на большой высоте существенно больше, чем у земной поверхности.

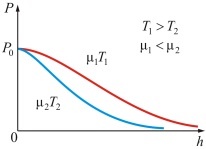
Графически закономерность можно изобразить с помощью двух кривых, которые трактуются, либо как соответствующие разным μ (при одинаковой Т), либо как отвечающие разным Т, при одинаковых μ. На графике видно, чем тяжелее газ (больше μ) и чем ниже температура, тем быстрее убывает давление.