Какое движение называют равномерным прямолинейным

Равномерное прямолинейное движение — что это в физике

Прежде чем перейти непосредственно к изучению понятия равномерного прямолинейного движения, необходимо рассмотреть его составляющие.

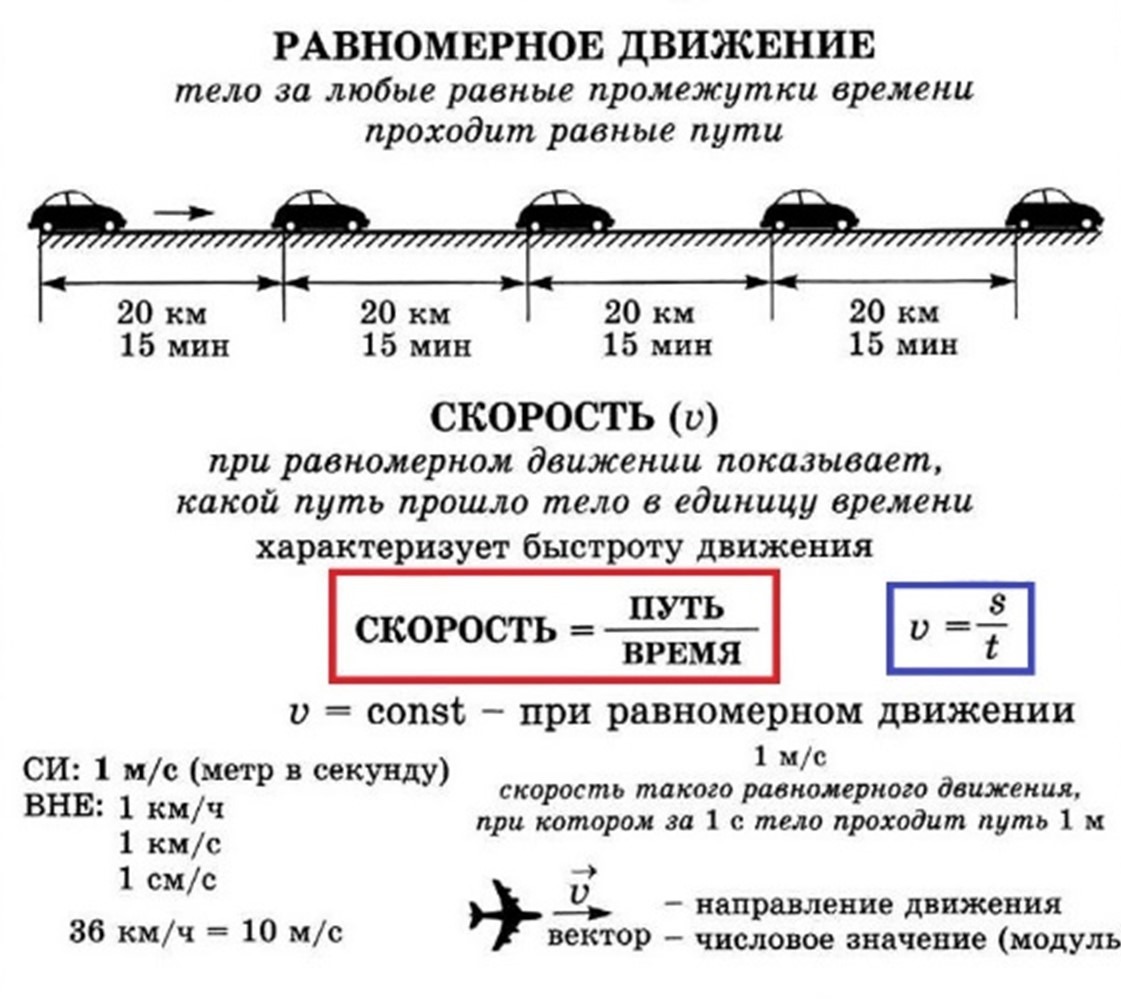
Равномерное движение практически невозможно в обычной жизни, поскольку для этого необходимы очень специфичные обстоятельства. На движущееся тело воздействует множество сил: тяжести, реакции опоры, трения, сила, под воздействием которой двигается тело. Чтобы тело двигалось равномерно, необходимо, чтобы эти силы были уравновешены определенным образом.

Также стоит учитывать особенность величины скорости, которая заключается в том, что скорость относительна и зависит от системы отсчета. Так, если человек движется в поезде, его скорость относительно поезда будет одной, а относительно статичных объектов вне поезда — другой.

Исходя из предыдущих определений и их отличительных признаков, можно вывести искомое.
 

Скорость такого движения постоянна и не зависит от времени. Ее вектор совпадает с вектором перемещения в каждой точке траектории.

\(v\;=\;const\)

Как записывается кинематический закон прямолинейного равномерного движения

Основная задача механики заключается в том, чтобы указать положение тела в пространстве в любой момент времени. Это помогает предсказать положение тела не только в настоящем, но и в любой момент в будущем. Выполнять эту цель помогает закон движения.
 

При равномерном прямолинейном движении тела по оси Ox за время t уравнение предстает в виде:

\(x\;=\;x_0\;+\;v_xt\;\)

Это уравнение следует из двух уравнений:

\(\Delta x\;=\;V_x\;,\) т.е.

\(\Delta x\;=\;x\;-\;x_0\)

Если тело движется противоположно положительному направлению оси \(O_x\), то проекция на ось отрицательна и считается, что скорость тела меньше нуля. Тогда уравнение принимает вид:

\(x\;=\;x_0\;-\;v_xt\;\)

Скорость при прямолинейном равномерном движении

Т. е. скорость движения тела показывает, какое перемещение совершает тело за единицу времени. Чем больше перемещение за определенный отрезок времени, тем больше скорость.

При прямолинейном равномерном движении скорость остается постоянной по модулю и направлению. Ускорение равно нулю.

В СИ главной единицей измерения скорости является 1 метр в секунду.

Сокращенно эту единицу обозначают как 1 м/с. Иногда используют дополнительные единицы:

• 1 км/ч = 1000 м/3600 с;
• 1 км/мин = 1000 м/60 с;
• 1 км/с = 1000 м/с;
• 1 м/мин = 1 м/60 с;
• 1 см/с = 0,01м/с.

Для измерения модуля скорости используют прибор спидометр.

Основные формулы

Перемещение является векторной величиной.

Скорость тоже является векторной величиной. Это значит, что она имеет не только модуль, но и направление.

При этом время не имеет направления, т. е. является скалярной величиной.

Исходя из определения, скорость равна перемещению, деленному на время, за которое это перемещение состоялось.

Запишем формулу в векторном виде:

\(\overrightarrow v=\frac{\overrightarrow s}t\)

Если направления скорости и перемещения не имеют значения для решения задачи, векторы можно не учитывать. Тогда вычисления со скоростью и перемещением производятся как с обычными скалярными величинами.

Выведем дополнительные формулы.

Векторное перемещение, или же скалярный пройденный при движении путь, равен скорости, умноженной на время.

\(\overrightarrow s=\overrightarrow v\cdot t \ или \overrightarrow s=\overrightarrow v\cdot t\;или\;s=v\cdot t\;\)

Тогда время, за которое тело со скоростью v переместилось на расстояние s, равно:

\(t=\frac{\overrightarrow s}{\overrightarrow v}\)

Примеры равномерного прямолинейного движения

Равномерное прямолинейное движение в жизни почти не встречается. Это идеализация, которая использует характеристики прямолинейного движения для упрощения расчета. Создать такие условия, чтобы тело могло достаточно долго двигаться с одинаковой скоростью, почти невозможно. Но движения в реальном, а не идеальном мире могут быть приближены к равномерному с некой степенью погрешности.

Ближе всего в природе к равномерному движению находится движение небесных тел в космосе, где они слабо взаимодействуют друг с другом, а воздействием других сил можно пренебречь.

Есть и другие примеры движения, которое близко к прямолинейному равномерному:

1. Автомобиль едет по прямой автомагистрали с постоянной скоростью.
2. Человек или другое живое существо идет по прямой дороге с неизменной скоростью.

Решение задач

Решение:

Вспомним формулу нахождения скорости при равномерном прямолинейном движении.

\(\overrightarrow v=\frac{\overrightarrow s}t\)

Выведем из нее формулу нахождения времени:

\(t=\frac{\overrightarrow s}{\overrightarrow v}\)

Произведем вычисления:

\(t=\frac{3\;км}{60\;км/ч}=\frac1{20}ч.\)

Ответ можно было бы записать в таком виде, но лучше привести их к единицам СИ, т. е. к секундам.

\(\frac1{20}ч\;=\;3\;мин\;=\;180\;с.\)

Ответ: 180 с.

Решение:

Запишем уравнение равномерного прямолинейного движения:

\(x\;=\;x_0\;+\;v_xt\;\)

Производить вычисления пока нельзя, т. к. единицы измерения величин различны. Переведем км/ч в м/с:\(18\;км/ч\;=\;\frac{18\cdot1000}{3600}=5\;м/с \)

Теперь найдем, где оказался спортсмен:

\(x\;=\;7\;м\;+\;5\;м/с\;\cdot\;3\;с\;=\;7\;м\;+\;15\;м\;=\;22\;м\)

Ответ: 22 м.