Как найти силу тяги

Что такое сила тяги

Действие силы тяги

Множество сил, действующих на движущийся объект, для упрощения вычислений делят на две группы: силу тяги и силы сопротивления.

Её прекращение

Когда действие силы тяги прекращается, движущееся тело замедляется и постепенно останавливается, так как на него воздействуют силы, мешающие продолжать двигаться, например, трение.

1 закон Ньютона о действии

Согласно этому закону в формулировке самого Ньютона, любое тело остается в покое или равномерно движется по прямой, пока на него не воздействуют силы, заставляющие его изменить это состояние.

В современной физике в формулировку внесены уточнения:

• закон применим только в системах отсчета, называемых инерциальными;
• тело может вращаться на месте, не находясь под воздействием внешних сил, поэтому вместо термина «тело» следует использовать термин «материальная точка».

Чтобы переместить неподвижный предмет, на него должна воздействовать некая сила. Чтобы изменить скорость движения предмета, также необходимо воздействие силы, замедляющей его или ускоряющей. Так как предметы обладают разной массой и соответственно разной инертностью, силы, достаточные для эффективного воздействия, тоже будут различаться.

Состояние ускорения после воздействия силы тяги

Когда движение равномерное, сила тяги и сила трения совершают одинаковую работу, уравновешивая друг друга. Воздействие силы на тело в направлении движения придает ему ускорение. Если направить ту же силу в противоположном направлении, она замедлит движение тела, что можно назвать отрицательным ускорением.

Формулы для определения силы тяги

Согласно второму закону Ньютона, сумма сил, воздействующих на движущееся тело, равна массе \(m\), умноженной на ускорение \(a\). Универсальной формулы, подходящей для любого сочетания сил, не существует. Чаще всего силу тяги находят с помощью общей формулы\( F_т-\;F_{с}=m\;\times\;a\), где \(F_т\) — сила тяги, \(F_{с}\) — силы сопротивления.
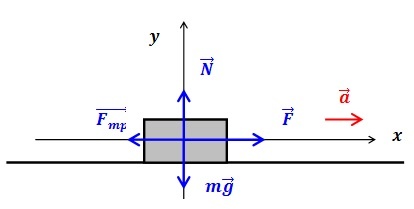
При решении конкретной задачи силы, воздействующие на тело, схематически изображают в виде векторов. На схеме:

• сила тяжести mg;
• сила реакции опоры \(N\);
• сила трения\( F_{тр}\);
• сила тяги \(F\). 

При нахождении тела на горизонтальной поверхности сила тяжести и сила реакции опоры уравновесят друг друга. Но если транспортное средство движется в гору или под гору, придется учесть влияние уклона. Тогда формула может выглядеть так: \(F_т-\;F_с-\;mg\;\times\;\sin\alpha=m\;\times\;a.\)

Какое условие должно соблюдаться

Сила тяги всегда должна быть больше противодействующих ей сил.

Формула через мощность

Полезную механическую мощность \(N\) можно вычислить по формуле \(N=F_т\;\times\;v\), где \(v\) — скорость. Для определения силы тяги нужно разделить мощность на скорость: \(F_т\;=\;\frac N v.\)

Измерение и обозначение силы тяги

Силу тяги обозначают \(F_т\) или \(F\). Единица измерения — ньютон (\(Н\)).
Для решения задач недостаточно измерить усилие, приложенное к объекту, и выразить его конкретным числом, так как сила обладает еще и направлением. Чтобы подчеркнуть, что сила — векторная величина, к буквенному обозначению добавляют стрелку.

Как определить силу тяги двигателя. Примеры решения задач

Задача 1

Автомобиль может разгоняться до 216 км/ч. Максимальная мощность двигателя равна 96 кВт. Определите максимальную силу тяги двигателя.

Решение

Переведем киловатты в ватты, а километры в час — в метры в секунду:

\(96\;\times\;1000=96000\;Вт\)

\(\frac{216\times1000}{3600}=60\frac мс\)

\(F_т\;=\;\frac N v = \frac{96000}{60} = 1600 Н\)

Задача 2

Троллейбус весом 12 тонн за 5 секунд проезжает по горизонтальной дороге 10 метров. Сила трения равна 2,4 кН. Определите силу тяги, которую развивает двигатель.

Решение

Переведем тонны в килограммы, а килоньютоны в ньютоны:

\(12\;\times\;1000=12000\;кг\)

\(2,4\;\times\;1000=2400\;Н\)

\(F_т-\;F_{тр}=m\;\times\;a\), следовательно, \(F_т=m\times a\;+\;F_{тр}\)

Чтобы определить ускорение а, воспользуемся формулой \(s\;=\;\frac{at^2}2\)

Подставив численные значения величин, получаем:

\(a\;=\;\frac{2s}{t^2}^{}=\frac{20}{25}\;=\;0,8\)

\(F_т=\;12000\times0,8\;+\;2400\;=\;12000\;Н\;=\;12\;кН\)

Задача 3

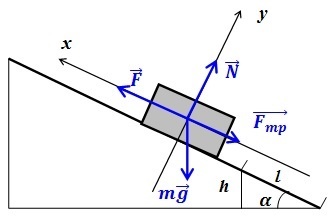
Транспорт, весящий 4 тонны, едет в гору. Уклон — 1 метр на каждые 25 метров пути. \(\mu\) — 0,1 от силы тяжести, \(а = 0\). Определите силу тяги.

Решение

Начертим схему:

\(m\times g\;+\;N\;+\;F_{тр\;}+\;F_т\;=\;m\times a\)

Сделаем проекции на координатные оси:

\(OX: -\;mg\;\times\;\sin\alpha\;-\;F_{тр\;}+\;F_т\;=\;0\)

\(OY: N\;-\;mg\;\times\;\cos\alpha\;=\;0 => N\;=\;mg\;\times\;\cos\alpha\;\)

\(F_{тр}\;=\;\mu N\;=\;\mu mg\;\times\;\cos\alpha\)

Подставим значение \(F_{тр}\) в уравнение \(OX\) и определим \(F_т\):

\(-mg\;\times\;\sin\alpha\;-\;\mu\)

\(mg\;\times\;\cos\alpha\;+\;F_т\;=\;0\)

\(=> F\;=\;mg\;\left(\sin\alpha\;+\;\mu\;\times\;\cos\alpha\right)\)

Найдем синус и косинус \(\alpha\), подставим их в общую формулу:

\(\sin\alpha\;=\;\frac hl\;=\;\frac1{25}\)

\(\cos\alpha\;=\;\frac{\sqrt{l^{2\;}-\;h^2}}l\;\)

\(F\;=\;\frac{4\;\times\;10^{3\;}\;\times\;9,8\;\times\left(1\;+\;0,1\;\sqrt{l^{2\;}-\;h^2}\right)}{25}\;=\;5,5\;\times\;10^3\;Н\;=\;5,5\;кН\)