Свойства дисперсии в физике
Что такое дисперсия
Статистическая дисперсия описывает разброс чисел в наборе данных по сравнению со средним или средним значением. Она рассчитывается путем умножения стандартного отклонения на квадрат.
Дисперсия — это мера изменчивости в статистике. Она оценивает среднюю квадратичную разницу между значениями данных и средним значением. В отличие от некоторых других статистических показателей изменчивости, она включает в свои расчеты все точки данных, противопоставляя каждое значение среднему.
При отсутствии изменчивости в выборке все значения одинаковы, и дисперсия равна нулю. По мере того как значения данных распространяются дальше, изменчивость увеличивается.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Существует два типа дисперсии:
- Популяционная: под популяцией понимается весь состав группы. Дисперсия популяции используется для определения того, как колеблется или распределяется каждая точка данных в конкретной популяции. Она рассчитывает квадратичное расстояние каждой точки данных от среднего значения популяции.
- Выборочная: трудно учесть каждую точку данных, если популяция слишком велика. В такой ситуации берется выборка точек данных из популяции, чтобы создать образец, который можно использовать для характеристики всей группы. В результате дисперсия выборки равна среднему квадрату отклонений от среднего. Для определения дисперсии всегда используется выборочное среднее.
Свойства дисперсии
Ниже приведены некоторые свойства дисперсии, которые можно использовать для решения как простых, так и сложных задач на сложение.
- Нулевая дисперсия указывает на то, что все точки сбора данных одинаково важны.
- Когда дисперсия велика, данные сильно разбросаны от среднего значения. С другой стороны, малая дисперсия указывает на то, что значения точек данных расположены ближе друг к другу и сгруппированы вокруг среднего значения.
- Var(X + C) = Var(X), где X — случайная переменная, а C — константа.
- Var(aX + b) = a2, где a и b — константы.
- Var(CX) = C2.
- Var(X), C — константа.
- Var(x1 + x2 +......+ xn) = Var(x1) + Var(x2) +........+Var(xn), где x1, x2, ......, xn — независимые случайные величины.
- Символ дисперсии обычно обозначается греческой буквой сигма-квадрат (σ²), когда речь идет о дисперсии популяции. Для дисперсии выборки она часто обозначается s².
Свойства математического ожидания и дисперсии
Если X — дискретная случайная величина, то ее ожидаемое значение (или среднее) — это средневзвешенное значение всех возможных значений, которые может принимать X, каждое из которых оценивается в зависимости от вероятности его появления. Обычно E(X) или m представляет собой ожидаемое значение X.
E(X) = S x P(X = x)
Другими словами, ожидаемое значение — это: [(каждый возможный исход) * (вероятность того, что исход произойдет)].
Ожидание — это то, что ожидается от результатов эксперимента в среднем.
Свойства среднего и дисперсии
Если X и Y — случайные величины, то E(X + Y) = E(X) + E(Y).
Если X1, X2, ... , Xn — случайные величины, то E(x1 + x2 +......+ xn) = E(X1) + E(X2) + ... + E(Xn) = Σi E(Xi).
Для случайных величин, X и Y, E(XY) = E(X) E(Y). И X, и Y здесь являются независимыми переменными.
Если X — случайная величина, а a — постоянная, то E(aX)= a E(X)и E(X + a) = E(X) + a.
Независимо от того, что является случайной величиной, если X > 0, то E(X) > 0.
E(Y) ≥ E(X), если X и Y таковы, что Y ≥ X.
Формулы
Существует две формулы для дисперсии. Правильная формула зависит от того, работаете ли вы со всей совокупностью или используете выборку для оценки значения совокупности. Другими словами, выбор формулы зависит от того, какую статистику вы используете — описательную (дескриптивную) или инференциальную.
Формула дисперсии популяции
Форму уравнения для популяции применяют, если есть значения для всех членов интересующей группы. В этом случае не используют выборку для оценки популяции. Вместо этого измеряют всех людей или предметы. Например, если вы измерили баллы за тест для всех членов класса и нужно узнать значение для этого класса, используйте формулу дисперсии популяции.
Формула дисперсии популяции выглядит следующим образом:
σ2 = ∑ (xi – x̄)2/n,
где σ2 — дисперсия популяции.
Xi — первая точка данных.
µ — среднее значение популяции.
n — количество наблюдений.
Чтобы найти дисперсию, возьмите одну точку данных, вычтите из нее среднее значение популяции и возведите разницу в квадрат. Повторите этот процесс для всех точек данных. Затем просуммируйте все эти квадраты и разделите на количество наблюдений. Таким образом, получается средняя квадратичная разница.
Статистики называют числитель в формуле дисперсии суммой квадратов.
Формула выборочной дисперсии
Если совокупность данных очень велика, становится трудно вычислить дисперсию совокупности данных. В этом случае мы берем выборку данных из заданной совокупности и находим дисперсию этой совокупности, которая называется выборочной дисперсией. При вычислении выборочного среднего мы обязательно вычисляем выборочное среднее, то есть среднее значение выборочного набора данных, а не среднее значение популяции. Дисперсию выборки можно определить как среднее квадратическое значение разницы между точкой данных выборки и средним значением выборки.
Например, если вы взяли случайную выборку студентов-статистиков, записали их результаты тестов и хотите использовать выборку в качестве оценки для совокупности студентов-статистиков.
Формула для популяции имеет тенденцию недооценивать изменчивость, когда ее используют с выборкой. Приведенная ниже формула выборки корректирует эту погрешность:
σ2 = ∑ (xi – x̄)2/(n – 1),
где s2 — выборочная дисперсия.
Xi — первая точка данных.
x̅ — выборочное среднее.
n-1 — число степеней свободы.
Процесс расчета для выборок очень похож на метод для популяции. Однако мы работаем с выборкой, а не с популяцией, и делим на n-1. Этот знаменатель противодействует смещению, когда выборки склонны занижать значение популяции.
Примеры
Найдите дисперсию следующего набора данных: 24, 54, 53, 36, 21, 84, 64, 34, 77, 53.
Решение:
x̄ = (24+54+53+36+21+84+64+34+77+53)/10
= 500/10
= 50.
| xi | (xi -x̄) | (xi – x̄)2 |
| 24 | -26 | 676 |
| 53 | 3 | 9 |
| 36 | -14 | 196 |
| 21 | -29 | 841 |
| 84 | 34 | 156 |
| 64 | 14 | 196 |
| 34 | -16 | 256 |
| 77 | 27 | 729 |
| 54 | 4 | 16 |
μx = Σxi/10=500/10=50 единиц;
σx = Σ(xi -x̄)2/10=4084/10= 408,4 единиц2.
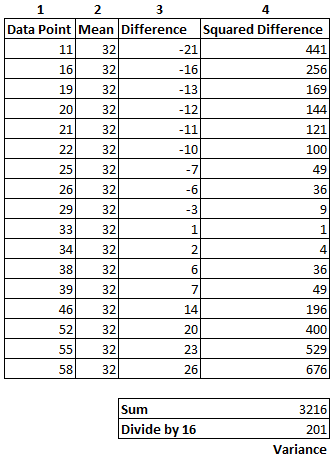
Набор данных содержит 17 наблюдений, которые представлены в таблице ниже. Числа в скобках соответствуют столбцам таблицы.
Чтобы рассчитать статистику, возьмите каждое значение данных (1) и вычтите среднее (2), чтобы вычислить разность (3), а затем возведите разность в квадрат (4).
В нижней части рабочего листа суммированы квадраты, их делят на 17 - 1 = 16, потому что мы находим выборочное значение.
Источник: statisticsbyjim.com
Дисперсия для этого набора данных равна 201.
Найдите дисперсию популяции для заданного набора данных X 21 42 37 16 31 28 33 41 12
Решение:
Среднее значение популяции = (21+42+37+16+31+28+33+41+12)/9 = 261/9 = 29.
Используем формулу дисперсии популяции:
[(21-29)2+(42-29)2+(37-29)2+(16-29)2+(31-29)2+(28-29)2+(33-29)2+(41-29)2+(12-29)2]/9
= 920/9 = 102,22 ед2.
Таким образом, популяционная дисперсия набора данных равна 102,22 ед2.
Вычислите количество наблюдений, если дисперсия данных равна 12, а сумма квадратов отклонений данных от среднего значения равна 156.
Решение:
Дано: (xi - x̄)2 = 156;
σ2 = 12.
Используя формулу для дисперсии, получаем:
σ2 = ∑ (xi - x̄)2/n;
12 = 156/n;
n = 156/12;
n = 13.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так