Движение тела, брошенного вертикально вверх

Что значит тело, брошенное вертикально вверх

В процессе изучения механики применяют разные физические законы и принципы, позволяющие описывать и исследовать движения материальных тел. В этот раздел включена пара направлений, то есть кинематика и динамика. Одним из типичных примеров задач на анализ перемещения объектов является вертикальный бросок какого-либо предмета.

Понять природу такого движения и разобраться в механизмах поведения тела, которое подбросили в вертикальном направлении вверх, поможет понятие свободного падения. Известно, что данное явление считают отдельным случаем равномерного передвижения объекта с ускорением при нулевом значении исходной скорости. Под ускорением здесь следует понимать ускорение свободного падения, которое в некоторых информационных источниках называют ускорением силы тяжести.

Перечислим несколько ключевых математических соотношений, описывающих ситуацию, когда тело падает свободно:

\(h = \frac{vt}{2}\)

\(h = \frac{at^{2}}{2}\)

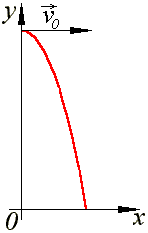
На координатной плоскости представлен наглядный график, описывающий изменение положения предмета, который пребывает в состоянии свободного падения:

Источник:  www.nivasposad.ru

В процессе ознакомления с теоретическим разделом по передвижению материальных тел и решения практических примеров необходимо обозначать физические величины согласно актуальным стандартам, к примеру:

• v обозначает скорость, с которой объект падает через некоторое время t;
• g является ускорением свободного падения;
• h вводят для обозначения высоты падения предмета;
• t стандартно фиксирует временной промежуток движения тела.

Особенность перемещения предмета, который подбросили в вертикальном направлении прямо вверх, заключается в том, что его движение отличается равномерностью и замедляется с некоторой исходной скоростью, обозначенной за \(v_{0}\), а также ускорением, равным а = -g. За кокой-то временной промежуток рассматриваемое тело преодолевает путь, то есть поднимается на высоту h. Запишем несколько математических закономерностей, применимых к процессу передвижения предмета, подброшенного в вертикальном верхнем направлении:

\(h = v_{0}t - \frac{gt^{2}}{2}\)

\(h = \frac{ v_{0} + v}{2} t\)

Введем обозначения для представленных выше выражений:

• \(v_{0}\) обозначает скорость тела в начале пути;
• v является скоростью, с которой предмет падает через некоторое время;
• g уже известно по предыдущему примеру и представляет собой ускорение свободного падения;
• h определяет высоту подъема подброшенного объекта;
• t служит обозначением для времени.

Используя введенные обозначения и ориентируясь на ранее записанные формулы, несложно сформулировать несколько важных математических соотношений. Такие выражения основаны на физических закономерностях и применимы к вычислению величин для объектов, подброшенных вертикально вверх. К примеру, для расчета скорости, которую приобретает предмет на определенной высоте, следует подставить известные данные в следующую формулу:

\(v = \sqrt{v_{0}^{2}-2gh}\)

В процессе своего перемещения материальное тело может подняться на высоту, определяемую с помощью данного выражения:

\(h_{max} = \frac{v_{0}^{2}}{2g}\)

Исходя из предыдущего соотношения, достаточно просто вывести справедливое равенство, описывающее время, в течение которого объект поднимался до того, пока не достиг максимальной высоты:

\(t_{hmax} = \frac{v_{0}}{g}\)

Скорость

Одним из ключевых параметров передвижения материального объекта, который подбросили вертикально вверх, является скорость. В зависимости от положения предмета, за которым ведется наблюдение, скоростная характеристика движения может отличаться. В связи с этим в формулах часто можно встретить сразу несколько обозначений скоростей, к примеру, исходную и ту, которую приобретает тело в конце пути.

Заметим, что допустимо участие объекта в поступательных движениях равного вида в одно и то же время. Исходя из того, что ускорение, скорость и передвижение рассматриваемого предмета представляют собой векторные величины, для вычисления их суммарных значений целесообразно воспользоваться закономерностями векторного сложения, знакомых еще с курса геометрии. Одним из таких принципов, который наиболее полезен в данном случае, является правило параллелограмма. С этой целью лучше заранее ввести несколько скоростных параметров:

1. \(v_{р}\) обозначает суммарную мгновенную скорость;
2. \(v_{1}\) представляет собой мгновенную скорость первого движения;
3. \(v_{2}\) необходима для обозначения мгновенной скорости второго движения.

Заметим, что между векторами первой и второй мгновенной скорости может формироваться некоторый угол. Тогда для расчета результирующей скоростной характеристики целесообразно применить следующую формулу:

\(v_{р} = \sqrt{v_{1}^{2} + v_{2}^{2} + 2v_{1}v_{2}\cos \alpha}\)

В том случае, когда первое и второе движения материального тела реализованы под углом в девяносто градусов относительно друг друга, то для вычисления скоростных параметров больше подходит данное математическое соотношение:

\(\cos (90^{0}) = 0\)

\(v_{р} = \sqrt{v_{1}^{2} + v_{2}^{2} }\)

Кинетическая энергия

Одним из интересных моментов для наблюдения является энергетический баланс для объекта, который подбросили вертикально вверх. Известно, что полная энергия тела состоит из потенциальной и кинетической. Рассмотрим алгоритм расчета кинетической энергии объекта, подброшенного в воздух, на примере типичной задачи из курса физики.

Предположим, что существует некоторое материальное тело, обладающее массой 200 гр. Данный предмет подбросили в вертикальном направлении вверх. Скорость этого действия составляет 30 м/с. Нужно вычислить величину кинетической энергии объекта, спустя 2 с после начала его пути. С помощью стандартных обозначений перепишем условия задания:

m=0,2 кг

\(\upsilon_0=30 м/с\)

t=2 с

Таким образом, по результатам расчетов должна получиться величина \(E_к\). В первую очередь выразим математически скорость \(\upsilon\) рассматриваемого объекта с использованием времени t:

\(\upsilon = {\upsilon _0} – gt\)

Получить значение кинетической энергии можно по стандартной формуле:

\({E_к} = \frac{{m{\upsilon ^2}}}{2}\)

Путем подстановки первого равенства в полученное соотношение величин выразим кинетическую энергию через время:

\({E_к} = \frac{{m{{\left( {{\upsilon _0} – gt} \right)}^2}}}{2}\)

Заметим, что все данные известны. Остается лишь подставить численные значения физических величин и рассчитать окончательный ответ:

\({E_к} = \frac{{0,2 \cdot {{\left( {30 – 10 \cdot 2} \right)}^2}}}{2} = 10 (Дж).\)

Формулы

Перед тем, как приступить к решению практических задач и отработке теоретических знаний, следует обобщить полученную информацию и записать основные положения и формулы. Подобный конспект поможет быстро ориентироваться в поисках ответов на задания и примеры любой сложности. Сформулируем ключевые принципы движения тела, которое подбросили вертикально вверх:

• перемещающийся таким образом предмет подвержен воздействию со стороны силы тяжести;
• объект при движении вниз ускоряется, а величина этого ускорения соответствует ускорению свободного падения;
• в процессе перемещения тела в верхнем вертикальном направлении подброшенное тело замедляется.

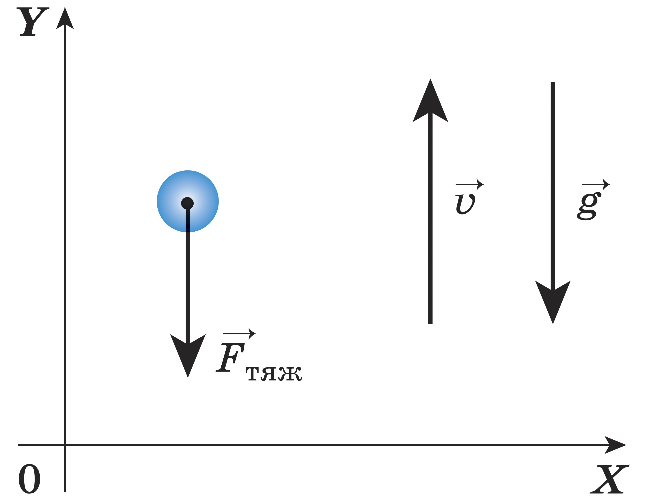
Перечисленные положения наглядно целесообразно представить на рисунке, где изображена координатная плоскость и продемонстрировано перемещение объекта с помощью стрелочек:

 

Источник: resh.edu.ru

Исходя из рассмотренного примера, можно выразить скорость материального тела через несколько справедливых равенств:

\(\overrightarrow{v} = \overrightarrow{v_{0}}+\overrightarrow{g}t\)

\(v_{0y}=v_{0}\)

\(g_{y}=-g\)

\(v_{y}=v_{0}-gt\)

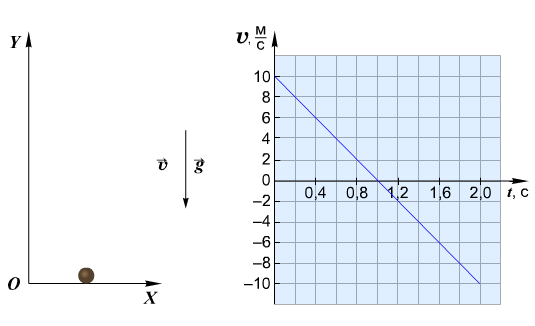
На графике соотношение между проекцией скоростной характеристики и временем в случае предмета, который подбросили вертикально вверх, представляет собой прямую линию. Ниже представлено графическое изображение зависимости этих величин:

 

Источник: resh.edu.ru

Проекция передвижения подброшенного вверх объекта определяется временной характеристикой, что хорошо видно по следующей формуле:

\(S_{y}=v_{0}t-\frac {gt^{2}}{2}\)

От временного параметра также зависит координата точки, в которой находится предмет. Сформулировать это соотношение физических величин целесообразно с помощью уравнения движения:

\(y = y_{0} + v_{0}t - \frac {gt^{2}}{2}\)

В процессе движения вверх по вертикали подброшенный объект достигает какой-либо максимальной высоты. Этот параметр несложно вычислить, зная начальную скорость. Задача легко решается с помощью следующего выражения:

\(h=\frac{v_{0y}^{2}}{2g}\)

Задачи

Решение

Воспользуемся уже известной формулой для вычисления времени полета подброшенного предмета. Подставив численные значения из условия задачи, получится без лишних преобразований оперативно посчитать ответ:

\(t = \frac{v_{0}+\sqrt{v_{0}^{2}+gh_{0}}}{g} = \frac{15+\sqrt{15^{2}+9,8\cdot 25}}{9,8} = 3,74\)

Ответ: 3,74 с.

Решение

Воспользуемся основными формулами, которые были записаны в теоретическом курсе. С помощью справедливых равенств и закономерностей достаточно просто вычислить физические величины, характерные для движения объекта, который подбросили вертикально вверх. Затем в буквенные выражения потребуется подставить числа, известные из условия задания. Выполним необходимые расчеты и запишем ответ:

\(H = h_{0}\frac{v_{0}^{2}}{2g} = 4 + \frac{10^{2}}{9,8} = 14,2 (м)\)

\(t = \frac{v_{0}+\sqrt{v_{0}^{2}+gh_{0}}}{g} =\frac{10+\sqrt{10^{2}+9,8\cdot 4}}{9,8} = 1,61 (c)\)

\(v_{2} = v_{k} = \sqrt{2gH} = \sqrt{2\cdot 9,8\cdot 14,2 } = 16,68 (м/с)\)

\(s = (H-h_{0}) + H = 2H - h_{0} = 2 \cdot 14,2 = 24,4 (м)\)

Ответ: \(H = 14,2 (м), t = 1,61 (c), v_{2} = 16,68 (м/с), s = 24,4 (м).\)

Решение

Известно, что в самой верхней точке, которую достигает подброшенный предмет, скорость имеет нулевое значение. Однако время пути в этом случае является неизвестной величиной. В связи с этим, с целью расчета высоты лучше воспользоваться следующим соотношением:

\(s = \frac{v^{2}-v_{0}^{2}}{-2g}\)

Путем подстановки численных величин в записанное выражение можно найти ответ к задаче:

\(s = \frac{0^{2}-10^{2}}{-2\cdot 10} = \frac{-100}{-20} = 5 (м)\)

Для удобства и упрощения расчетов ускорение свободного падения в данном случае было принято за 10. Заметим, что по условию примера объект подбросили не с поверхности земли, а с возвышенности. По этой причине нужно найти общую высоту:

5 + 2 = 7 (м)

Ответ: 7 м.