Основные условия равновесия тел
Что значит равновесие тел
Равновесием называют такое положение тела, когда оно пребывает в покое по отношению к инерциальной отсчетной системе.
Равновесное состояние объектов является актуальным вопросом и нуждается в детальном изучении. На этом явлении основаны многие основные процессы в физике. Благодаря полученным знаниям, активно развиваются наука и технологии. Принципы равновесия нашли применение при подготовке проектов и планов работ в строительстве, альпинизме, гимнастике, хореографии и других направлениях. Особый интерес представляют условия, когда выведенные из равновесного положения тела падают или остаются неподвижными.
Равновесие изучают в рамках отдельного курса механики. Раздел статики посвящен исследованию явления, характерного для тел, которые пребывают в состоянии равновесия и являются абсолютно твердыми. Таким образом, с точки зрения статики, тело считается полностью твердым, то есть не может быть деформировано. Стоит уточнить, что в данном случае деформационные изменения сильно малы, поэтому не подлежат учету.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Известно, что центром тяжести обладают все без исключения тела. Допустимо, когда рассматриваемая точка расположена за пределами объекта. Тогда закономерно возникает вопрос относительно правильности формирования подвеса или подпорки для тела, что в результате должно уравновесить его положение. Пример такой задачи рассматривал в прошлом Архимед. Исследователь ввел в обиход понятия плеча силы и момента силы. Сформулируем эти определения.
Плечо силы представляет собой протяженность перпендикулярной прямой, которая соединяет ось вращения и линию действия силы.
Моментом силы называют величину в физике, которая вычисляется, как результат умножения силы по модулю на плечо этой силы.
По итогам проведенных изысканий Архимед представил условие, при котором рычаг принимает положение равновесия. Закономерность принимает следующий математический вид записи:
\(\frac{F_{1}}{F_{2}} =\frac{d_{2}}{d_{1}} \)
Заметим, что записанное выше равенство подтверждено установленными ранее закономерностями. При доказательстве справедливости представленной формулы использован Второй закон Ньютона. Таким образом, соотношение является следствием этой закономерности.
Какие условия необходимы для равновесия тел
Исходя из вышесказанного, можно заключить, что равновесное положение тела приобретают при определенном условии. Первым условием является нулевое значение суммы всех сил, которые воздействуют на рассматриваемый объект. Соотношение, описывающее это положение, примет следующий вид:
\(\sum \overrightarrow{F} = 0\)
Заметим, что правильная запись условия равновесного положения тела предполагает векторный формат и наличие знака операции суммирования.
Второе условие равновесного состояния объекта заключается в сложении моментов всех сил, действующих на тело извне по отношению к любой оси, с нулевым итогом. Таким образом, справедливо следующее уравнение:
\(М_{1} + М_{2} + М_{3} + … = 0\)
Интерес представляет ситуация, когда предмет обладает некоторой опорной площадью. При этом тело пребывает в равновесном положении при условии, что вертикальная прямая пересекает центр тяжести этого объекта и расположена в пределах площади его опоры.
Одной из мировых достопримечательностей считают наклонную башню в итальянском городе Пизе. Даже визуально заметно отклонение сооружение относительно прямой оси. Однако постройка под углом не разрушается уже долгое время. Это объясняется особым расположением центра тяжести объекта. Вертикаль, проходящая по центру тяжести, находится внутри опорной площади этого объекта.
В реальных условиях важно учитывать не только непосредственно равновесное положение тела, но и качественный параметр рассматриваемого состояния. Данная характеристика называется устойчивостью. Исходя из озвученного показателя, выделают три типа равновесия, а именно:
- устойчивое;
- неустойчивое;
- безразличное.
Когда тело отклоняется от равновесного состояния, можно наблюдать проявление силы или момента силы, которые стремятся вернуть объект в равновесное положение. В этом случае целесообразно говорить об устойчивом равновесии.
Неустойчивое равновесие подразумевает возникновение обратной ситуации. При этом тело отклоняется от равновесного состояния, а возникающие силы или моменты сил способствуют увеличению наблюдаемого отклонения.
Третий вариант равновесия является безразличным. В таком случае в условиях небольшого отклонения объект остается стабильным, то есть не меняет равновесное состояние на противоположное.
В действительности в процессе строительства зданий и сооружений необходимо ориентироваться на устойчивое равновесие объектов. С этой целью инженеры производят точные расчеты габаритов и нагрузок, чтобы исключить даже минимальные риски нарушения равновесного положения. В противном случае строения с крупными размерами становятся опасными и не допускаются к дальнейшей эксплуатации.
Задачи
Представим, что имеется какая-то однородная лестница. Пусть эта конструкция опирается на вертикально расположенную стену с гладкой поверхностью. В результате между ними образован угол, равный \(\alpha\) . Примем коэффициент трения между разными поверхностями лестницы и полом за \(\mu\). Нужно вычислить наибольшее значение для \(\alpha\), при котором лестница пребывает в состоянии покоя.
Решение
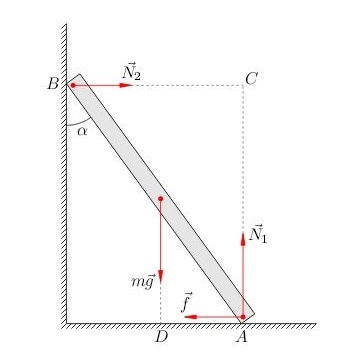
Упростить задачу можно с помощью выполнения наглядного изображения описанной в условии системы тел, которая включает в себя лестничную конструкцию, пол, стену. Обозначим за опорные точки А и В. Затем выполним расстановку сил, оказывающих действие на объект в виде лестницы.
Источник: ege-study.ru
В условиях задания речь идет об однородной лестнице. В таком случае сила тяжести, выраженная через \(m\overrightarrow{g}\), воздействует на середину конструкции. При этом сила упругости пола \(\overrightarrow{N_{1}}\) и сила трения \(\overrightarrow{f}\) приложены к точке А. На изображении видно, что точка приложения сил несколько смещена от точки А во внутреннее пространство лестницы. В результате допустимо прийти к выводу о приложении сил к лестнице непосредственно, а не к полу.
Аналогичным образом сила упругости \(\overrightarrow{N_{2}}\) приложена в точке В. В связи с тем, что стена обладает гладкой поверхностью, сделаем вывод о нулевом значении силы трения между стеной и лестничной конструкцией. Вспомним первое условие для равновесного положения тела. Если рассматривать ось по горизонтали, то сформулировать равновесие сил можно с помощью соотношения:
\(f = N_{2}\)
По вертикали наблюдается следующее состояние равновесия приложенных к телу сил:
\(mg = N_{1}\)
Далее стоит перейти к правилу моментов, то ест второму условию, при котором тело принимает положение равновесия. Возникает вопрос с корректным выбором оси. Целесообразно использовать ось, которая пересекает точку А, то есть расположена перпендикулярно относительно плоскости изображения.
При этом одновременно моменты сил \(\overrightarrow{f}\) и \(\overrightarrow{N_{1}}\) принимают нулевые значения, та как плечи рассматриваемых сил по отношению к точке А равны нулю. Это связано с прохождением линии воздействия сил сквозь эту точку.
Какими-либо значениями обладают моменты сил \(m\overrightarrow{g} и \overrightarrow{N_{2}}\) относительно точки А. Эти силы стараются придать лестнице вращательное движение в разные стороны. Тогда моменты рассматриваемых сил должны быть взаимно равны.
Используя сделанные ранее логичные заключения, продолжим расчеты. Заметим, что плечо силы \(\overrightarrow{N_{2}}\) является длиной перпендикуляра АС, который выходит из точки А к линии ВС действия силы \(\overrightarrow{N_{2}}\). Плечо силы \(m\overrightarrow{g}\) представляет собой протяженность перпендикуляра AD, который выходит из точки А к линии действия силы \(m\overrightarrow{g}\). Воспользуемся правилом моментов и зафиксируем справедливое соотношение:
\(N_{2}\cdot АС = mg \cdot AD\)
Предположим, что в длину лестничная конструкция составляет 2l. При этом условии получим, что:
\(АС = 2l \cos\alpha\)
\(AD = l \sin \alpha\)
Путем подстановки преобразуем предыдущее выражение для моментов:
\(N_{2}\cdot 2l \cos\alpha = mg \cdot l \sin \alpha\)
Таким образом, получим следующее справедливое равенство:
\(2 N_{2} = mg \tan\alpha\)
Объединим первое и последнее выражения для получения следующего равенства:
\(2f = mg \tan\alpha\)
Решение задачи призвано определить самое большое значение угла \(\alpha\). При таком условии лестница пребывает в равновесном состоянии, но при малейшем воздействии может соскользнуть с опорной поверхности. Исходя из вышесказанного, целесообразно заключить, что сила трения f обладает максимально возможным значением, равным силе трения скольжения. Таким образом:
\(f = \mu N_{1}\)
Далее выполним преобразования и вычислим искомое значение угла:
\(2 \mu N_{1} = mg \tan\alpha\)
\(2 \mu mg = mg \tan\alpha\)
\(\alpha = \arctan (2 \mu)\)
Ответ: максимальное значение угла составляет \(\arctan (2 \mu)\) .
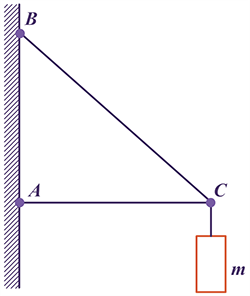
Требуется рассчитать значение момента силы тяжести груза, который имеет массу 40 кг и закреплен на подвесе в виде кронштейна АВС по отношению к оси, пересекающей точку В. При этом длина отрезка АВ составляет 0,5 м, а величина угла \(\alpha\) равна 45°.
Источник: resh.edu.ru
Решение
Воспроизведем в памяти понятие момента силы. По определению его величина вычисляется, как результат от умножения модуля силы на ее плечо. Формула имеет следующий вид:
M = Fd
В первую очередь нужно вычислить, чему равно плечо силы. С этой целью требуется провести перпендикулярную прямую, соединяющую опорную точку с линией действия силы. Плечо, характерное для силы тяжести, составляет длину отрезка АС. Исходя из того, что величина угла равна 45°, справедливо соотношение:
АС = АВ
При вычислении модуля силы тяжести целесообразно воспользоваться формулой:
F = mg
Путем подстановки численных значений получим следующее решение:
\(F = 40 \cdot 9,8 = 400 Н\)
\(М = 400 \cdot 0,5 = 200 Н \cdot м\)
Ответ: \(200 Н \cdot м\)
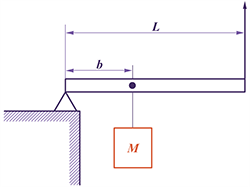
В процессе изображения сил, действующих на тело, на рисунке отметили вертикально ориентированную силу F. Рассматриваемый груз весит 100 кг. Положение этого предмета уравновешено путем закрепления на рычаге. В состав рычажной конструкции входит шарнир без трения и однородный массивный стержень длиной L=8 м. Точка, в которой подвешено тело, удалена от шарнирной оси на расстояние b=2 м. Требуется вычислить модуль силы F при условии равенства массы рычага 40 кг.
Источник: resh.edu.ru
Решение
Заметим, что в задании речь идет о ситуации, когда рычажная конструкция пребывает в равновесном положении. Описать этот случай поможет второе условие равновесия. Подставим в стандартное выражение для суммы значения из условия задачи, получим:
\(M \cdot g \cdot b + 0,5 \cdot m \cdot g \cdot L = FL\)
Из записанного соотношения несложно вывести формулу для расчета силы:
\(F = \frac{M \cdot g \cdot b + 0,5 \cdot m \cdot g \cdot L }{L }\)
Подставим численные значения и продолжим вычисления:
\(F = \frac{100 \cdot 9,8 \cdot 2 + 0,5 \cdot 40 \cdot 9,8 \cdot 8 }{8 } = 450 H\)
Ответ: 450 H.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так