Внутренняя энергия: первый закон термодинамики
Что такое внутренняя энергия в термодинамике
Наука термодинамика изучает тепловые явления. По сравнению с молекулярно-кинетической теорией, заключения которой основаны на знаниях о молекулярной структуре вещества, в термодинамике принимают во внимание общепринятые законы, описывающие тепловые процессы и применение характеристик макроскопических систем.
В данном случае выводы построены на комплексе фактов, сформулированных опытным путем, и не связаны со сведениями о внутреннем составе вещества. С другой стороны, во многих ситуациях термодинамика опирается на основы молекулярно-кинетические модели с целью наглядной демонстрации заключений.
Предметом изучения в термодинамике являются изолированные системы тел, которые пребывают в состоянии термодинамического равновесия. Подобные условия формируются в том случае, когда не наблюдаются макроскопические явления. Одним из ключевых свойств системы в равновесии с точки зрения термодинамики служит выравнивание температурных параметров каждой из ее частей.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
При стороннем воздействии на термодинамическую систему можно наблюдать в итоге переход этой системы в другое состояние равновесия. Этот процесс является термодинамическим. В случае низкой скорости течения рассматриваемого процесса в какой-либо временной момент система приближается к равновесию. Квазистатическими процессами называют такие, которые состоят из последовательности положений равновесия.
Одним из важных определений в термодинамике считают внутреннюю энергию. При рассмотрении этого понятия необходимо понимать, что любое из макроскопических тел наделено энергией, которая заключена внутри этих тел непосредственно.
Исходя из принципов молекулярно-кинетической теории, внутренняя энергия вещества состоит из кинетической энергии, заключенной во всех атомах и молекулах, а также потенциальной энергии их взаимодействия.
В процессе изучения понятия внутренней энергии в термодинамике рассматривают частный случай идеального газа. Внутренняя энергия данного вещества представляет собой сумму кинетической энергии каждой из составных частиц, которые постоянно движутся в неопределенных направлениях, то есть прибывают в состоянии теплового движения. Этот параметр определяется температурными характеристиками вещества и не обладает зависимостью от объема, что отражено в законе Джоуля.
Согласно положениям молекулярно-кинетической теории, внутренняя энергия 1 моля идеального газа с одним атомом, к примеру, гелия или неона, молекулы в котором движутся поступательно, вычисляется по формуле:
\(U=\frac{3}{2}N_{A}kT=\frac{3}{2}RT\)
Зная, что имеется определенная зависимость между потенциальной энергией взаимодействия молекул и расстоянием, на которое эти молекулы удалены друг от друга, можно сделать вывод о зависимости внутренней энергии объекта не только от температурных параметров, но и от объема. Данное заключение допустимо записать в виде уравнения:
\(U = U(T,V)\)
В результате внутренняя энергия тела однозначно определяется макроскопическими характеристиками состояния, в котором пребывает рассматриваемое тело. Параметр не меняется в зависимости от способа формирования этого состояния. В термодинамике принято рассматривать внутреннюю энергию, как функцию состояния. Таким образом, подобная характеристика может менять значение в том случае, когда силы, оказывающие на тело воздействие извне, совершают какую-либо работу.
Свойства
При рассмотрении свойств внутренней энергии целесообразно принять это понятие за компонент полной энергии. Исходя из этого, перечислим следующие свойства внутренней энергии:
- Внутренняя энергия представляет собой индифферентный скаляр. Важно заметить, что к ней не относят кинетическую энергию, которой обладают система в виде единого целого и внутренняя среда системы. К таковым причисляют энергию смещения простейших областей в процессе деформирования твердых объектов, энергию потоков жидких и газообразных сред.
- Внутренняя энергия является аддитивной величиной. Смысл этого утверждения состоит в равенстве внутренней энергии системы суммарным величинам внутренних энергий, характерных для подсистем.
- Внутреннюю энергию определяют с точностью до неизменяемого слагаемого, которое зависит от заданного отчетного нуля и не влияет на величину изменения внутренней энергии, полученной путем измерений в процессе экспериментов.
Предположим, что имеется некий закупоренный сосуд с небольшим количеством воды на дне. Если в него закачивать воздух, то, спустя определенное время, крышка будет выдавлена давлением. При этом в сосуде формируется туман. Если проанализировать описанное явление, то можно прийти к выводу о том, что воздух внутри резервуара обладал некоторой силой. Когда пробка вылетела, воздухом совершалась работа. С другой стороны, такая возможность характерна лишь для объектов, имеющих энергетический запас. Исходя из вышесказанного, можно заключить, что воздух в сосуде обладал определенной энергии.
Первый закон термодинамики, формулы
С помощью первого начала термодинамики конкретизируют общую физическую закономерность, описывающую явление сохранения энергии в случае термодинамических систем. Согласно традиционному подходу, первое начало представляет собой отношение, формулирующее взаимосвязь внутренней энергии, работы и теплоты.
Согласно пониманию У. Томсона первое начало термодинамики представляют в виде дефиниции внутренней энергии для закрытых систем. Таким образом, внутренняя энергия U в некотором процессе изменяется на величину, вычисляемую путем суммирования количества тепловой энергии Q, участвующей в обмене между системой и внешней средой, и работы A , которую совершает непосредственно рассматриваемая система, либо произведенной над этой системой: \(\Delta U\equiv Q+A\).
Проанализировав математическое соотношение, можно заметить, что в данном случае допустимо использовать термодинамический принцип знаков для теплоты и работы. Применительно к этим величинам, в термодинамике оперируют определениями из смежных физических направлений. С другой стороны, понятие количества чистоты используют лишь в термодинамике.
Исходя из вышесказанного, целесообразно определять первое начало термодинамики по Клаузиусу. Тогда теплоту рассчитывают по известным величинам внутренней энергии и работы. В таком случае формула примет следующий вид:
\(Q\equiv \Delta U+A \)
Если воспользоваться принципом знаков для теплоты и работы, то следует поменять знак у работы А на противоположный. Тогда соотношение будет записано таким образом:
\(Q\equiv \Delta U-A.\)
Задачи
Аэростат обладает объемом \(500 м^{3}\). Конструкция заполнена газообразным веществом, роль которого играет гелий. Давление во внутренней среде, состоящей из газа, равно 105 Па. Когда аэростат нагревается под лучами солнца, температурный режим внутри повышается с отметки в 10°C до значения в 25°C. Необходимо выяснить, на какую величину изменилась внутренняя энергия газообразной среды.
Решение
Из курса теории вспомним, что гелий является одноатомным газом. В таком случае допустимо применить в процессе решения задания соотношение, характеризующее внутреннюю энергию следующего формата:
\(U_{1}=\frac{3}{2}\frac{m}{M} RT_{1}\)
По условию примера заметим, что температура повышается и достигает второго значения. Запишем для него формулу:
\(U_{2}=\frac{3}{2}\frac{m}{M} RT_{2}\)
Тогда целесообразно представить запись соотношения, описывающего процесс, когда изменяется величина энергии:
\(\Delta U = U_{2} - U_{1} =\frac{3}{2}\frac{m}{M} R(T_{2} - T_{1})\)
Заметим, что для вычисления искомого значения необходимо определить, чему равна масса. Узнать, сколько весит гелий в конкретном случае не представляется возможным. В связи с этим, целесообразно воспользоваться закономерностью Менделеева-Клапейрона, описывающей связь между исходной температурой, сформированным давлением и объемом газообразного вещества:
\(\frac{m R}{M} = \frac{pV}{ T_{1}}\)
Путем подстановки записанного соотношения в ранее выведенную формулу получим следующее справедливое равенство для расчета искомой величины:
\(\Delta U = \frac{3}{2}pV(\frac{ T_{2} }{ T_{1}}- 1) \approx 4\cdot 10^{6} Дж.\)
Ответ: внутренняя энергия изменится на \(4\cdot 10^{6} Дж\).
Цилиндрический объект установили под увесистый поршневой механизм. Рассматриваемый цилиндр заполнен углекислым газом, молярная масса которого составляет 0,044 кг/мoль. Масса газообразного вещества равна 200 гр. Изменение температуры среды можно определить, как 88 K. Нужно вычислить величину совершаемой в процессе работы.
Решение
Заметим, что в описанной ситуации рассматривается расширение газообразного вещества при определенном и неизменном давлении, сформированным внешней атмосферной средой и поршневой установкой. Тогда целесообразно записать работу газа в виде следующего соотношения:
\(A' = p(V2 - V1)\)
Здесь V1 и V2 обозначают объем газообразной среды в начале и конце анализируемого процесса. Воспользуемся уже знакомым принципом Менделеева-Клапейрона, чтобы выразить произведения давления и объема, зафиксированные на разных этапах. Подставим полученные соотношения в формулу работы:
\(A' = \frac{m R}{M} (Т2 - Т1) \approx 3,3 Дж.\)
Ответ: газ совершает работу, равную 3,3 Дж.
Газ совершает некую работу в процессе сжатия. Количество вещества составляет 3 моль. В результате температурный режим повысился на 100 К. Требуется вычислить, какую работу совершал газ, без учета тепловых потерь.
Решение
В первую очередь следует рассмотреть описанный в задаче процесс. Сжатие происходит при совершении внешней силой положительной работы. Таким образом, внутренняя энергия меняется, как и температура газообразного вещества. Запишем озвученное соотношение:
\(А = \Delta U\)
Далее следует обратиться к формуле, описывающей то, как меняется внутренняя энергия:
\(\Delta U = \frac{3}{2}vR\Delta T\)
Таким образом, путем подстановки записанного выражения в соотношение, определяющее работу, можно вычислить ее значение:
\(А = -\frac{3}{2}vR \Delta T \approx -1250 Дж.\)
Ответ: работа, которую совершал газ под давлением, составляет -1250 Дж.
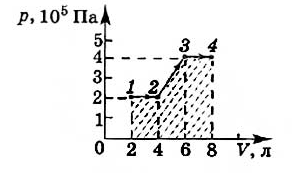
В процессе изменения состояния газообразного вещества меняются значения его давления и объема. Описать взаимную зависимость данных характеристик можно с помощью графика. На рисунке для наглядности продемонстрирована связь этих величин. Необходимо определить, чему равна работа газа.
Источник: class-fizika.ru
Решение
Заметим, что для вычисления работы в данном случае целесообразно определить значение площади, которой характеризуется закрашенная область на графике. На изображении с первого по второй и с третьего по четвертый отмечены изобарные процессы. Исходя из этой информации, запишем пару выражений для работы, совершаемой газом:
\(А _{1-2}= р_{1}(V_{2}-V_{1})\)
\(А _{3-4}= р_{2}(V_{4}-V_{3})\)
Отдельно нужно рассмотреть переход со второго этапа на третий. В процессе наблюдается изменение всех трех параметров. В связи с этим, запишем формулу для расчета работы:
\(А _{2-3}= \frac{р_{1}+р_{2}}{2} (V_{3}-V_{2})\)
Проанализируем изменение объема газообразного вещества. В таком случае получим:
\(V_{2} — V_{1} = V_{3} — V_{2} = V_{4} — V_{3} = \Delta V\)
Исходя из полученного выше соотношения, запишем выражение для расчета работы:
\(А = (р_{1}+р_{2}+\frac{р_{1}+р_{2}}{2}\Delta V = \frac{3}{2}(р_{1}+р_{2}) \Delta V = 1800 Дж.\)
Ответ: работа газа составляет 1800 Дж.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так