Энергия электростатического поля в физике

Что такое энергия электростатического поля

В процессе изучения такой категории как энергия электрического поля в курсе физики обязательно предстоит познакомиться с процессами формирования ее запасов и условиями для энергетических расходов. Удобнее всего рассматривать понятие и его характеристики с помощью анализа работы электроконденсаторов. Это яркий пример накопления значительного энергетического объема в достаточно ограниченном пространстве.

Отдельного внимания заслуживают экспериментальные опыты, демонстрирующие широкие возможности применения генерируемой энергии и взаимодействия с ней в реальных условиях на практике. Благодаря установленным принципам и закономерностям статики, человечество достигло существенного прогресса в плане технологического развития. Начать процесс изучения следует с терминологии.

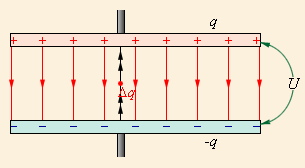
При наличии пары проводников, обладающих зарядом, как в конденсаторе, суммарная энергия рассматриваемой системы вычисляется путем суммирования индивидуальных потенциальных энергий проводников и энергии, с которой эти проводники взаимодействуют. Далее озвученное соотношение будет описано с помощью математического уравнения, а схематично процесс изображен на рисунке:

Источник: www.phyzika.ru

Формулы, от чего зависит

Представим, что имеется некоторый воздушный электроконденсатор. Запишем соотношение величин для выражения энергии этой установки:

\(W = \dfrac{CU^2}{2}=\dfrac{\varepsilon_0S}{d}\dfrac{(Ed)^2}{2}=\dfrac{\varepsilon_0E^2}{2}Sd\)

Заметим, что в данном случае целесообразно воспользоваться следующим справедливым равенством для вычисления объема рассматриваемого конденсатора:

Sd = V

В результате простых преобразований получим следующее соотношение:

\(W=\dfrac{\varepsilon_0E^2}{2}V\)

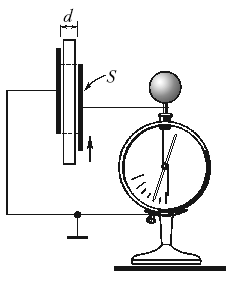
Наглядное изображение электроконденсатора представлено на рисунке ниже:

Источник: fiz.1sept.ru

В результате несложных расчетов можно наблюдать, как формируется энергия электрического поля в рамках определенного объема. Исходя из этого положения, допустимо сделать вывод о наличии у электрического поля собственной энергии. В качестве примеров того, как энергетический запас расходуется и распространяется, целесообразно привести радиоволны и свет от Солнца. Это наглядное представление переноса энергии на огромные расстояния посредством электромагнитных волновых потоков.

Отдельно можно рассмотреть ситуацию, при которой конденсатор заполняют диэлектриком определенной плотности. В подобных условиях емкость установки будет увеличена в \(\varepsilon\) раз. Тогда выведенное математическое соотношение следует преобразовать и записать таким образом:

\(W=\dfrac{\varepsilon_0\varepsilon E^2}{2}V\)

Заметим, что величина энергии электрического поля определяется свойством диэлектрической проницаемостью, которой обладает изучаемая среда. Представленные соотношения величин применимы не только для решения задач в рамках электростатики. Записанные формулы позволяют характеризовать электрические поля, изменяющиеся в определенные временные интервалы.

Примеры решения задач

Решение

При условии известного значения емкости конденсатора допустимо определить разность потенциалов между его пластинами:

\(С =\frac{q}{U}\)

\(U =\frac{q}{C}\)

По итогам несложных математических преобразований можно определить искомую напряженность, подставив известные по условию задачи значения физических величин:

\(Е =\frac{U}{d} =\frac{q}{Cd} =\frac{10^{-8}}{2 \cdot 10^{-8} \cdot 5 \cdot 10^{-3}} = 100\)

Ответ: 100 В/м.

Решение

\(W = \frac{CU^{2}}{2}\)

\(U = \sqrt{\frac{2W}{C}} = \sqrt{\frac{2\cdot 2 \cdot 10^{-3}}{10 \cdot 10^{-6}}} = 20\)

Ответ: 20 В.