Энергия электрического поля

Что такое энергия электрического поля

Физик Майкл Фарадей сделал следующие выводы об электрическом поле:

1. Каждый заряд формирует вокруг себя электрическое поле определенной мощности.
2. Электрическое поле воздействует на другой заряд с определенной силой.

Электрическое поле обладает рядом свойств:

• поле материально;
• источником является заряд;
• обнаружить поле можно, исходя из действия на заряд;
• поле распределяется непрерывно в пространстве;
• при удалении от заряда поле слабеет.

Тело, обладающее зарядом, действует на другие тела, притягивая и отталкивая их. По отношению к заряженному объекту другие тела поворачиваются и перемещаются. Для любого электрического поля характерен запас энергии. В случае исчезновения электрического поля его электроэнергия трансформируется обратно в работу.

Энергия заряженного конденсатора

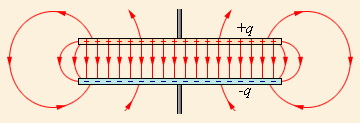
Компоненты конденсаторов в виде проводников обозначают обкладками. Наиболее простым примером конденсатора является совокупность двух плоских пластин. Данные элементы способны проводить электрический ток и расположены параллельно относительно друг друга. Пластины удалены на небольшое по сравнению с их габаритами расстояние и отделены диэлектрическим материалом.

В плоском конденсаторе можно наблюдать электрическое поле:

1. Основное — в области между пластин.
2. Слабое или поле рассеяния — около краев пластин и во внешней среде.

Опытным путем было доказано, что конденсатор, обладая электрическим полем, вмещает определенный запас энергии. Для ее расчета необходимо найти сумму работы внешних сил, необходимых для питания конденсатора. Такой процесс является последовательным переносом минимальных порций заряда Δq > 0 с одном пластины на другую.

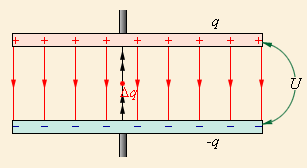
Один элемент при этом будет постепенно приобретать положительный заряд, а другой — заряжаться отрицательно. Транспортировка заряда осуществляется при условии, что пластины уже обладают неким зарядом q. Разность потенциалов между ними будет определена по формуле:

\(U=\frac{q}{C}\)

В процессе переноса некоторого заряда Δq вешние силы совершают работу, которая определяется следующим уравнением:

\(\Delta A=U\Delta q=\frac{q\Delta q}{C}\)

Энергию We конденсатора, емкость которого составляет С, а заряд равен Q, можно рассчитать с помощью интегрирования предыдущей формулы в пределах от 0 до Q:

\(W_{e}=A=\frac{Q^{2}}{2C}\)

Следует учитывать следующее условие:

\(Q=CU\)

Тогда энергия заряженного конденсатора будет переписана в другом эквивалентном уравнении:

\(W_{e}=A=\frac{Q^{2}}{2C}=\frac{CU^{2}}{2}=\frac{QU}{2}\)

Электрическая энергия \(We\) будет рассматриваться в качестве потенциальной энергии, которая находится в запасе заряженного конденсатора. Для расчета электрической энергии справедливо применять формулу, с помощью которой определяют потенциальную энергию деформированной пружины \((Ер)\):

\(E_{p}=\frac{kx^{2}}{2}=\frac{F^{2}}{2k}=\frac{Fx}{2}\)

Где k является жесткостью пружины, \(х\) — деформацией, а \(F = kx\) равно внешней силе.

Исходя из современных представлений, электрическую энергию можно наблюдать в области между пластинами конденсатора, то есть в пространстве с электрическим полем. Отсюда появилось название энергии электрического поля.

Как рассчитать энергию электрического поля через напряженность, формула

В качестве примера можно рассмотреть плоский конденсатор. Его однородное электрическое поле в этом случае будет обладать напряженностью. Данная величина определяется по формуле:

\(E=\frac{U}{d}\)

Емкость конденсатора будет рассчитываться таким образом:

\(C=\frac{\varepsilon _{0}\varepsilon S}{d}\)

Исходя из приведенных равенств, энергия электрического поля будет равна:

\(W_{e}=\frac{CU^{2}}{2}=\frac{\varepsilon _{0}\varepsilon SE^{2}d^{2}}{2d}=\frac{\varepsilon _{0}\varepsilon E^{2}}{2}V\)

Где V = Sd является объемом пространства между пластинами конденсатора, который вмещает электрическое поле.

Объемная плотность электрической энергии

Расчет физической величины We выглядит следующим образом:

\(W_{e}=\frac{\varepsilon _{0}\varepsilon E^{2}}{2}V\)

Таким образом, \(We\) представляет собой электрическую или потенциальную энергию единицы объема пространства, в котором сформировано электрическое поле. Данная величина — объемная плотность электрической энергии. Для того чтобы найти энергию поля, созданного путем распределения электрически заряженных частиц в пространстве, необходимо интегрировать объемную плотность по всему объему, для которого характерно наличие электрического поля.