Основные логические операции
Логические операции в создании компьютерных программ — действия, которые производятся над входными данными. Такие функции производятся над сигналами булевского типа, то есть над примитивными выражениями, имеющими только два возможных значения: истина или ложь.
Виды операций
В программировании выделяют следующие виды функций:
- Логическое умножение или конъюнкция.
- Логическое сложение или дизъюнкция.
- Логическое отрицание или инверсия.
- Логическое следование или импликация.
- Логическая равнозначность или эквивалентность.
- Стрелка Пирса.
- Штрих Шеффера.
Логическое умножение (конъюнкция)
Конъюнкция — это действие, в результате которого каждым двум входным данным соответствует одно новое высказывание. Истинное значение на выходе получается, когда оба входных значения истинны.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Для обозначения логического умножения используют союз «и», значки\( \wedge\), \(\&.\)
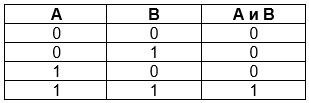
Таблица истинности для логического умножения выглядит так:
A, B — исходные данные;
A и B — значение, приобретаемое в результате реализации конъюнкции.
Из таблицы следуют свойства логического умножения:
- при ложном значении одной входной информации из двух конъюнкция будет ложной;
- при истинном значении переменных конъюнкция будет истинной;
- результат логического умножения не зависит от порядка записи ее переменных.
Логическое сложение (дизъюнкция)
Дизъюнкция — это булева функция, в итоге которой выходные данные будут ложными только при ложности всех исходных выражений.
Обозначается дизъюнкция союзом «или», символами +,\( \vee\).
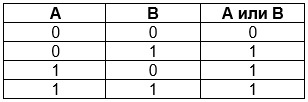
Таблица истинности логического сложения:
A, B — входная информация;
A или B — значение, приобретаемое в результате выполнения дизъюнкции.
Для дизъюнкции справедливы следующие утверждения:
- при истинности хотя бы одного подвыражения дизъюнкция будет истинной;
- при ложности всех высказываний дизъюнкция примет ложное значение;
- итог дизъюнкции не зависит от перемены мест слагаемых.
Логическое отрицание (инверсия)
Инверсия — выражение, ставящее в соответствие одному значению противоположное.
Условное обозначение логического отрицания: с помощью частицы «не», символов ¯, \(\neg.\)
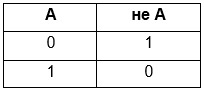
Таблица истинности инверсии:
A — исходные данные;
не A — значение, приобретаемое в результате логического отрицания.
Логическое следование (импликация)
Импликация — это булева операция, ложная лишь тогда, когда первая исходная переменная является истиной, а вторая — ложью.
Следование записывается с помощью знака \(\rightarrow.\)
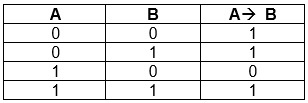
Таблица истинности для импликации:
A — входная информация, означающая условие;
B — входная информация, означающая следствие;
A → B — значение, приобретаемое в результате импликации.
По своему употреблению данная связка схожа со значением союзов «если..., то...».
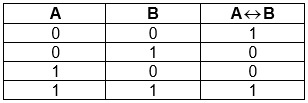
Логическая равнозначность (эквивалентность)
Эквивалентность — выражение, являющееся истинным лишь в случае равенства двух входных элементов.
При записи равнозначности используют стрелки \(\Leftrightarrow\), \(\leftrightarrow\), \(\Xi\).
Таблица истинности для равнозначности:
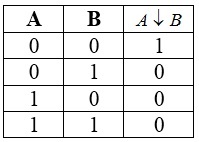
Стрелка Пирса
Стрелка Пирса — двухместное логическое действие со следующей последовательностью: сначала над исходными показаниями производится дизъюнкция, затем происходит отрицание полученного результата.
Данная манипуляция является отрицание логического сложения. Свое название рассматриваемая функция получила от своего автора — американского ученого Чарльза Пирса.
Запись стрелки Пирса осуществляется через знак \(\downarrow\).
Таблица истинности для этой операции следующая:
Особенность стрелки Пирса заключается в ее возможности строить другие булевы функции.
Пример
\((A\;\downarrow\;A)\;\downarrow\;(B\;\downarrow\;B)\;=\;A\;\wedge\;B\) — конъюнкция;
\((A\;\downarrow\;B)\;\downarrow\;(A\;\downarrow\;B)\;=\;A\;\vee\;B\) — дизъюнкция;
\(A\;\downarrow\;A\;=\;\neg\;A\;\) — инверсия;
\(((A\;\downarrow\;A)\;\downarrow\;B)\;\downarrow\;((A\;\downarrow\;A)\;\downarrow\;B)\;=\;A\;\rightarrow\;B\) — импликация.
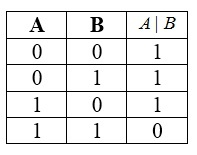
Штрих Шеффера
Штрих Шеффера — это действие, приводящее к ложному итогу лишь при истинности обоих исходных данных. По порядку выполнения операций эта функция эквивалентна отрицанию конъюнкции.
Символ Шеффера назван по фамилии своего создателя — американского логика Генри Шеффера — и обозначается посредством знака \(\vert.\)
Таблица истинности для данной функции:
С помощью штриха Шеффера можно воспроизвести другие логические манипуляции.
Пример
\((A\;\vert\;B)\;\vert\;(A\;\vert\;B)\;=\;A\;\wedge\;B\) — конъюнкция;
\((A\;\vert\;A)\;\vert\;(B\;\vert\;B)\;=\;A\;\vee\;B \) — дизъюнкция;
\(A\;\vert\;A\;=\;\neg\;A \) — инверсия.
Порядок выполнения операций
В составном логическом выражении действия выполняются в такой последовательности:
- инверсия;
- конъюнкция;
- дизъюнкция;
- импликация;
- эквивалентность.
Для построения нужного порядка, как и в математических выражениях, используют скобки.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так