Как перевести числа из одной системы счисления в другую
Порядковый счет в разных системах
Десятичная
Сама запись чисел связана с определенной числовой базой. Видя число 105, мы понимаем, что цифра 1 задает число сотен, 0 — число десятков, 5 — единиц. Элементы числовой базы, или ключевые числа, в десятичной системе счисления представляют собой степени десяти: \(10 = 10^1\), \(100 = 10^2\), \(1000 = 10^3\).
В системе всего десять цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Число 10 — основание системы счисления. Цифры от 0 до 9 представляют собой коэффициенты разложения числа по степеням десяти.
Родина десятичной системы счисления — Индия. Примерно в середине 8 века систему стали использовать другие страны. В Европе она распространилась к 16 веку и была названа «арабской».
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Двоичная
Система счисления, в которой в качестве базовых чисел выбираются степени числа 2, называется двоичной. Чтобы не путать их с числами, записанными в десятичной системе счисления, справа внизу указывают основание системы счисления. Обычно число при этом заключают в скобки.
\({(12)}_{10\;}\;=\;{(1100)}_2\)
Так как самая распространенная система счисления — десятичная, ее основание обычно не указывают. Поэтому пример может выглядеть и так:
\(12\;=\;{(1100)}_2.\)
Двоичную систему использовали задолго до возникновения информационных технологий. Единица обозначает наличие сигнала, ноль — его отсутствие, на этом были построены примитивные сигнальные системы, прообразы азбуки Морзе.
Пятеричная
Связана с количеством пальцев на одной руке, использовалась в Китае и у некоторых племен Африки. В китайском языке у иероглифов, обозначающих цифры от 6 до 9, был один и тот же знак в начале — сокращенное обозначение цифры 5. Для записи чисел в этой системе используются цифры 0, 1, 2, 3, 4.
Перевод десятичных чисел в другие системы счисления
Согласно теории чисел, в общем случае представить произвольное число N в системе счисления с заданным основанием d означает записать его в виде \(N\;=\;a_n\times d^n\;+\;a_{n-1}\times d^{n-1}\;+\;...\;+\;a_2\times d^{2\;}+\;a_1\times d\;+\;a_0\).
Представим число N в виде выражения, не содержащего степеней:
\(N\;=\;а_{0\;}+\;d\times(a_1\;+\;d\times(a_2\;+\;d\times(...\;+\;d\times(a_{n-1}\;+\;d\times a_n)...)))\)
Очевидно, что цифры \(а_{0\;},\;a_1,\;a_2,\;...,\;\;a_n\;\) можно найти последовательно, начиная с младшего разряда, совершив следующие шаги:
-
\(а_{0\;}\) равно остатку от деления N на d;
-
\(а_{1\;}\) равно остатку от деления на d неполного частного, полученного на предыдущем шаге;
-
…;
- \(а_{n\;}\) равно остатку от деления на d неполного частного, полученного на предыдущем шаге.
Число N в d-ичной системе будет выглядеть так:
\(N = {(а_na_{n-1}\;...\;a_1a_0)}_d\)
Для записи чисел в системе с основанием d нужно d цифр. Если d меньше или равно 10, то в качестве алфавита используются арабские цифры, если больше — к ним добавляют 26 латинских букв.
Практический перевод чисел
Перевод чисел из десятичной системы счисления в другую удобнее всего производить методом деления на основание новой системы счисления.
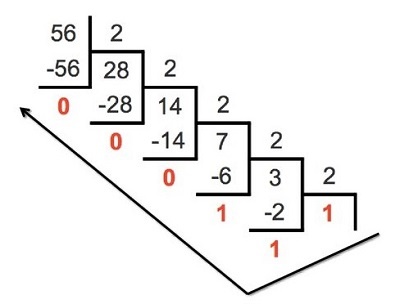
Чтобы перевести исходное число в десятичной системе в двоичную, нужно делить его, а также получающиеся в процессе деления частные на 2, пока в итоге не получится 1. Промежуточные остатки при этом следует отмечать отдельно. Число, образованное последним частным 1 и остатками, перечисленными справа налево, будет искомым.
\( {(56)}_{10} = {(111000)}_2\)
Перевод из любой системы в десятичную
Формулировка
Если все слагаемые недесятичного числа записать в развернутой форме в десятичной системе и сложить по правилам десятичной арифметики, то получится число в десятичной системе, равное данному недесятичному.
Анализ записи в любой системе
Основа перевода чисел в десятичную систему — разложение их по разрядам. Записав число в виде многочлена, расположенного по степеням основания, и найдя значение этого выражения, можно перевести в десятичную систему число из любой системы.
Разложим по разрядам число \({(235)}_8\).
\({(235)}_8 = 2\times8^2\;+\;3\times8\;+\;5\;=\;157\)
Примеры перевода чисел в разных системах счисления
Задача 1
Перевести шестнадцатеричное число \(AF_{16}\) в десятичную систему.
Решение
Чтобы получить десятичное представление числа, нужно записать обе его цифры в развернутой форме.
\(AF_{16}\;=\;A\times16^{1\;}\;+\;\;F\times16^0\;=\;10\times16\;+\;15\;=\;175\)
Задача 2
Перевести число 176 из десятичной системы в троичную, пятеричную и четырнадцатеричную.
Решение
Перевод в троичную систему:
176 : 3 = 58 (2)
58 : 3 = 19 (1)
19 : 3 = 6 (1)
6 : 3 = 2 (0)
\({(176)}_{10}\;=\;{(20112)}_3\)
Перевод в пятеричную систему:
176 : 5 = 35 (1)
35 : 5 = 7 (0)
7 : 5 = 1 (2)
\({(176)}_{10}\;=\;{(1201)}_5\)
Перевод в четырнадцатеричную систему:
176 : 14 = 12 = С (8)
\({(176)}_{10}\;=\;{(С8)}_{14}\)
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так