Значение магнетона бора

Что такое магнетон бора

Применение

Применяется в различных областях физики, таких как физика твердого тела, ядерная физика и астрофизика.

Является важнейшим фактором при определении магнитных свойств материалов. Он используется для расчета магнитных моментов атомов и молекул, которые, в свою очередь, определяют магнитное поведение материалов. Магнитные моменты материалов также можно сравнить с магнетоном Бора, чтобы определить их относительную силу и поведение в магнитных полях.

Имеет широкий спектр практических применений, в том числе при проектировании и разработке магнитных устройств хранения данных, таких как жесткие диски и кредитные карты. Он также используется в медицинских методах визуализации — МРТ, в спектроскопии ЯМР.

Теория

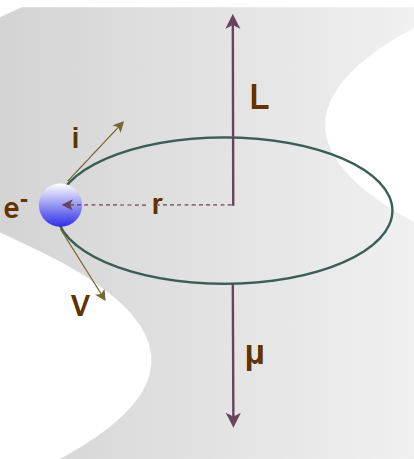
Магнитный момент электрона в атоме состоит из двух компонентов. Во-первых, орбитальное движение электрона вокруг ядра генерирует магнитный момент по циркулярному закону Ампера. Во-вторых, присущее электрону вращение или спин, создает спиновый магнитный момент.

В боровской модели атома для электрона, находящегося на орбите с наименьшей энергией, его орбитальный угловой момент имеет величину, равную уменьшенной постоянной Планка, обозначаемой ħ. Магнетон Бора — это величина магнитного дипольного момента электрона, вращающегося по орбите атома с этим угловым моментом.

Спиновый угловой момент электрона равен 1/2ħ, но собственный магнитный момент е^-, обусловленный его спином, также приблизительно равен одному магнетону Бора, в результате чего спиновый g-фактор (фактор Ланде) электрона, коэффициент, связывающий спиновый угловой момент с соответствующим магнитным моментом частицы, имеет значение приблизительно 2.

Орбитальный и спиновый моменты е^-:

Состояние электрона на атомной орбитали определяется четырьмя квантовыми числами n, /, mi, ms, где n = 1, 2, 3,---;/ = 0, 1, 2, - - - , n - 1; m, = -/,-/ + 1, ■ ■ -, l - l, 1; ms = - s, s с s = 1/2. Орбитальный угловой момент - L с собственным значением km/, спиновый угловой момент - S с собственным значением hms. Орбитальный магнитный момент равен M, = -xBL, а спиновый магнитный момент равен Ms = -где g = 2,0023 ~ 2 (фактор Ланде или электронный спектроскопический фактор). Таким образом, полный магнитный момент электрона равен Mf = -mb(L + gS).

История

1. Вальтер Ритц (1907) и Пьер Вейс ответственны за концепцию элементарных магнитов. Несколько исследователей предположили, что магнетон должен иметь постоянную Планка h еще до появления резерфордовской модели строения атома.
2. Постулируя, что отношение кинетической энергии электрона к орбитальной частоте должно быть равно h, Ричард Ганс в 1911 году вычислил значение, которое было в два раза больше магнетона Бора.
3. В 1911 году румынский физик Стефан Прокопиу открыл выражение для магнитного момента электрона. В румынской научной литературе это значение часто называют «магнетоном Бора-Прокопиу».
4. В 1911 году был открыт магнетон Вейсса — единица магнитного момента, равная 1,531024 джоуля на теслу, или около 20% магнетона Бора.
5. В результате создания модели атома датский физик Нильс Бор летом 1913 года получил значения натуральных единиц атомного углового момента и магнитного момента.

Как вычислить среднее число магнетонов бора

Формула

Магнетон Бора — это единица магнитного момента, равная заряду электрона, умноженному на его уменьшенную постоянную Планка и разделенному на удвоенную массу.

В единицах СИ магнетон Бора определяется как в гауссовых единицах СГС (сантиметр-грамм-секунда). Чтобы вычислить магнетон Бора, используется формула μB = eħ/2me, где e — элементарный заряд, ħ — уменьшенная постоянная Планка, I — масса электронов, c — скорость света.

Единицами измерения магнетона Бора являются джоули на теслу (J/T) или амперы на квадратный метр (A-m²).

Чтобы перевести джоули на теслу в амперы на квадратный метр, нужно умножить на 1,2566370614 x 10^-6.

Магнетон бора и магнитный момент

Источник: geeksforgeeks.org

Является векторной величиной. Объекты имеют тенденцию располагаться таким образом, что вектор магнитного момента становится параллельным линиям магнитного поля.
Направление магнитного момента указывает с южного на северный полюс магнита. Магнитное поле, создаваемое магнитом, прямо пропорционально магнитному моменту.

Электроны, вращающиеся вокруг ядра, аналогичны круговому контуру с током. Этот ток создает магнитный дипольный момент, пропорциональный орбитальному угловому моменту электрона. Поскольку орбитальный угловой момент квантуется в терминах уменьшенной постоянной Планка, дипольный момент квантуется в магнетоне Бора. Значение магнетона Бора равно 9,274 x 10^-24 Am² (или 5,788 x 10^-5 электронвольт на теслу). Электроны также обладают собственным спиновым угловым моментом, и связанный с ним спиновый магнитный момент составляет примерно один магнетон Бора. Орбитальный и спиновый угловой момент объединяются векторно и дают чистый магнитный момент материала. Векторная сумма этих моментов определяет магнитные свойства материалов.

Рассмотрим пример, в котором требуется определить намагниченность насыщения для железа. Неизвестная величина может быть оценена с помощью известных величин, таких как атомный вес железа 55,8 amu, плотность 7,87 г/см3 и чистый магнитный момент на атом 2,2 магнетона Бора.

Теперь число атомов в единице объема материала определяется следующим выражением:

число атомов в единице объема = (плотность x число Авогадро) / атомная масса

Подставив известные значения плотности, числа Авогадро и атомной массы в приведенное выше выражение, получим число атомов в единице объема, равное 0,849 x 10²³ атомов/см³.

Теперь магнитный момент одного атома составляет 2,2 магнетона Бора. Использование значения магнетона Бора дает значение магнитного момента на атом 20,394 x 10^-24 Am².

Наконец, намагниченность насыщения равна числу атомов в единице объема, умноженному на магнитный момент на атом. В результате расчетное значение намагниченности насыщения для железа составляет 1,7314 Am².

Примеры решения задач

Решение:

Для этого мы можем воспользоваться формулой: μ = μB * S, где μB — магнетон Бора, S — спин электрона. Если спин электрона равен 1/2, то магнитный момент электрона будет равен 1/2 μB.

Решение:

Тогда энергия магнитного диполя в магнитном поле может быть найдена по формуле: E = -μ * B * cos(θ), где θ — угол между магнитным моментом и направлением магнитного поля.

Решение:

Энергия спин-орбитального взаимодействия электрона в атоме водорода равна Eso = μB * B * (1 / r^3), где μB — магнетон Бора, B — магнитное поле, r — радиус орбиты.

Энергия магнитного взаимодействия электрона с ядром: Em = −2μB * B.

Приравнивая эти две энергии, получаем μB * B * (1 / r^3) = −2μB * B.
Отсюда r = (2)^(1/3) * a0, где a0 — боровский радиус, равный приблизительно 0.529 * 10^(-8) см.
Таким образом, расстояние, на котором энергия спин-орбитального взаимодействия становится больше, чем энергия магнитного взаимодействия электрона с ядром в атоме водорода, составляет примерно 1.195 * 10^(-8) см.

Решение:

Для атома водорода спиновый квантовый числов S электрона равен 1/2, а его орбитальный момент равен l=0, так как водородный атом имеет только один электрон. Согласно формуле для вычисления магнитного момента μ электрона в атоме водорода:
μ = -g * μB * √(S * (S+1)),
где g — фактор Ланде, равный 2 для электрона, μB — магнетон Бора, S — спиновый квантовый числов электрона.

Подставим известные значения и получим:
μ = -2 * μB * √(1/2 * (1/2+1)).
μ = -2 * μB * √(1/2 * (3/2)).
μ = -2 * μB * √(3/4).
μ = -2 * μB * √3/2.

Получается, магнитный момент атома водорода составляет -√3/2 * μB.