Алгебраическая форма записи комплексного числа

Что такое алгебраическая форма записи комплексного числа

Здесь действительное число а — действительная часть числа z:

а=Re z

где а действительное число, b — его мнимая часть: b=Im z.

Величина i — это мнимая единица, которая удовлетворяет равенству:

i²=-1.

Сделаем изображение КЧ на комплексной плоскости.

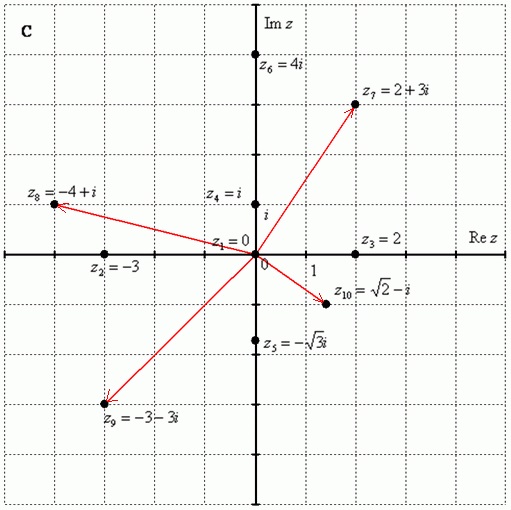
С — множество КП. Комплексная плоскость состоит из двух осей: Re z — действительная ось, Im z — мнимая ось. Чтобы правильно оформить данную плоскость, нужно задать масштаб по осям, отметить ноль, единицы для действительной и для мнимой осей. Построим несколько показательных точек:

\(z_1=0\), \(z_2=-3\), \(z_3=2\), \(z_4=i\), \(z_5=-\sqrt3i\), \(z_6=4i\),\( z_7=2+3i\), \(z_8=-4+i\),\( z_9=-3-3i\), \(z_10=\sqrt2-i\).

Числа \(z_1=0\), \(z_2=-3\), \(z_3=2 \) — КЧ с нулевой мнимой частью.

Числа \(z_4=i\), \(z_5=-\sqrt3i\), \(z_6=4i\) — это чисто мнимые числа, то есть числа с нулевой действительной частью. Они находятся строго на мнимой оси Im z. 

В числах \(z_7=2+3i\), \(z_8=-4+i\), \(z_9=-3-3i\), \(z_{10}=\sqrt2-i\) и действительная, и мнимая части не равняются нолю. Они обозначаются точками на комплексной плоскости. Также к ним проводят радиус-векторы из начала координат. На чертеже они показаны красным цветом. Радиус-векторы к числам, располагающимся на осях, не чертят, так как они сливаются с осями.

Сложение, вычитание, умножение и деление комплексных чисел, записанных в алгебраической форме

Сложение и вычитание КЧ следует совершать по правилам сложения и вычитания многочленов, то есть, раскрывая скобки и приводя подобные. Делается это согласно формулам:

• \(z_1\;+\;z_2\;=\;x_1\;+\;i\;y_1\;+\;x_2\;+\;i\;y_2\;=\;x_1\;+\;x_2\;+\;i\;(y_1\;+\;y_2)\)
• \(z_1\;–\;z_2\;=\;x_1\;+\;i\;y_1–\;(x_2\;+\;i\;y_2)\;=\;x_1–\;x_2\;+\;i\;(y_1–\;y_2)\)

Произведение КЧ производится по правилам умножения многочленов. При этом важно учитывать, что \( i^2=-1\). Тогда мы получаем:

\(z_1\;z_2\;=\;(x_1\;+\;i\;y_1)\;(x_2\;+\;i\;y_2)\;=\;x_1x_2\;+\;i\;x_1\;y_2\;+\;i\;y_1x_2\;+\;i\;{}^2\;y_1\;y_2\;=\;=\;x_1x_2\;+\;i\;x_1y_2\;+\;i\;y_1x_2\;–\;y_1\;y_2\;=\;x_1x_2\;–\;y_1\;y_2\;+\;i\;(x_1\;y_2\;+\;i\;x_2\;y_1)\)

Деление КЧ осуществляется на число, не равное нолю. Делается это с использованием формулы:

\(\frac{z_1}{z_2}=\frac{x_1iy_1}{x_2iy_2}=\frac{\left(x_1+iy_1\right)\left(x_2-iy_2\right)}{\left(x_2+iy_2\right)\left(x_2-iy_2\right)}=\frac{x_1x_2-ix_1y_2+iy_1x_2-i^2y_1y_2}{{x^2}_2+{y^2}_2}=\frac{x_1x_2+y_1y_2}{{x^2}_2+{y^2}_2}+i\frac{x_2y_1-x_1y_2}{{x^2}_2+{y^2}_2}\)

Преобразование комплексных чисел в алгебраическую форму

Как упоминалось выше, преобразовать КЧ в алгебраическую форму можно с помощью формулы: z=a+bi. Рассмотрим это действие на примерах.

Задача 1

Записать \(z=\frac{3+i}5\) в алгебраической форме. Определить, чему равняются действительная и мнимая части.

Решение

Почленно поделим дробь: 

\(z=\frac{3+i}5=\frac35+\frac i5=\frac35+\frac15i\)

Тогда: \(Re\;z=\frac35,\;Im\;z=\frac15\).

Ответ: \(Re\;z=\frac35,\;Im\;z=\frac15.\)

Задача 2

Перевести \(z=\frac{7-i}4+13\) в алгебраическую форму, найти его мнимую и действительную части и сопряженное число.

Решение

Применяем почленное деление и правило сложения дробей:

\(z=\frac{7-i}4+13=\frac74+13-\frac i4=\frac{59}4-\frac14i\)

В таком случае \(Re\;z=\frac{59}4,\;Im\;z=-\frac14\).

Сопряженное число, то есть число вида \(\overline z=x-iy\), равно \(\overline z=\frac{59}4+\frac14i\).

Ответ: \(Re\;z=\frac{59}4,\;Im\;z=-\frac14, \overline z=\frac{59}4+\frac14i.\)