Как найти арктангенс: формула, функция, свойства
Понятие арктангенса
Арктангенс для числа х является значением угла у, которое определено в радианах и характеризуется \(\operatorname {tg} y=x,\quad -{\frac {\pi }{2}}\)
Область определения для функции \(y=\operatorname {arctg}x\) распространяется на всю прямую с числами, не прерывается и обладает ограничениями. Такая функция строго возрастает на графике.
\(\operatorname {tg}\,(\operatorname {arctg}\,x)=x, если при x\in {\mathbb R},\)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
\(\operatorname {arctg}\,(\operatorname {tg}\,y)=y\), когда если \(-{\frac {\pi }{2}}<y<{\frac {\pi }{2}}\),
\(D(\operatorname {arctg} \,x)=(-\infty ;\infty )\) (область определения),
\(E(\operatorname {arctg}\,x)=\left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right)\) (область значений).
Функция arctg обладает следующими свойствами, которые полезно использовать при расчете:
- \(\operatorname {arctg}(-x)=-\operatorname {arctg}x\qquad \)(функция не является четной);
- \(\operatorname {arctg} x=\arcsin {\frac {x}{\sqrt {1+x^{2}}}}\);
- \(\operatorname {arctg}x=\arccos {\frac {1}{{\sqrt {1+x^{2}}}}},\) если \(x > 0\);
- \(\operatorname {arctg} x=\operatorname {arcctg} {\frac {1}{x}}\);
- \(\operatorname {arctg} x=-i\operatorname {arth} {ix}\), при \(\operatorname {arth}\) в виде обратного гиперболического тангенса, гиперболического ареатангенса.
- \(\operatorname {arth} x=i\operatorname {arctg} {ix}\).
Получение функции арктангенса
Предположим, что имеется некая функция:
\(y=\operatorname {tg}\,x\).
Заметим, что эта функция имеет вид кусочно-монотонной. Такая ситуация наблюдается на любом участке области определения. В результате нельзя назвать функцией:
\(y=\operatorname {arctg}\,x\)
Это связано с нарушением условий однозначности. Проанализируем участок, где функция является возрастающей и имеет каждое значение лишь однажды:
\(\left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right).\)
Отрезок \(y=\operatorname {tg}\,x\) отличается тем, что здесь функция является монотонно возрастающей со всеми своими значениями, которые она принимает только однажды.
Можно сделать вывод, что на отрезке \(\left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right)\) имеется обратная функция \(y=\operatorname {arctg}\,x \) с графиком, симметричным графическому изображению \(y=\operatorname {tg}\,x\) на участке \(\left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right)\) по отношению к прямой \(y=x\).
График арктангенса
Рассматриваемая аркфункция характеризуется определенным графиком. Изобразить арктангенс на координатной плоскости можно с помощью преображения графика, которому соответствует тангенс. В процессе требуется переместить между собой оси абсцисс и ординат.
Необходимо избавиться от многозначности. Для этого следует ввести ограничение на множество из значений функции в виде интервала: \(- frac{pi}2 leqslant y leqslant frac{pi}2\). На этом отрезке функция характеризуется монотонностью. Такой интервал носит название основного значения арктангенса.
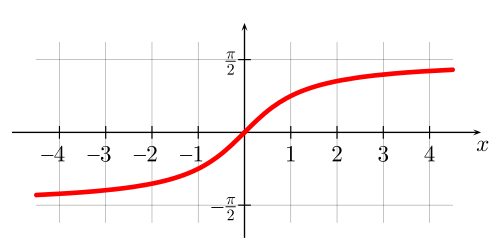
График функции \(y=\operatorname {arctg}\,x\) (можно построить в программе Эксель при вводе нужной формулы):
Арксинус, арккосинус, арктангенс и арккотангенс как число
Обратными функциями в тригонометрии называют такие функции, которые являются обратными к тригонометрическим функциям.
Существует несколько основных аркфункций:
- арксинус, \(\arcsin x\), представляет собой угол, синус которого определен, как \(х\);
- арккосинус, \(\arccos x\), в виде угла с косинусом \(х\);
- арктангенс, \(\operatorname {arctg} x\), или \({\displaystyle \arctan x}\);
- арккотангенс, \(\operatorname {arcctg} x\), или \(\operatorname {arccot} x\), или \(\operatorname {arccotan} x\);
- арксеканс, \(\operatorname {arcsec} x\);
- арккосеканс, \(\operatorname {arccosec} x\), или \(\operatorname {arccsc} x\).
Обратные тригонометрические функции обладают особыми наименованиями. Названия аркфункций формулируют путем приписывания к наименованию функции приставки «арк-».
Функции в тригонометрии отличаются периодичностью. В связи с этим обратные к ним функции обладают множеством значений в виде углов (дуг), для которых конкретная прямая функция определена соответствующим числом.
Под функцией \(\arcsin 1/2\) понимается множество углов \(\left ( \frac{\pi}{6}, \frac{5 \pi}{6}, \frac{13 \pi}{6}, \frac{17 \pi}{6} \dots ~ (30^\circ, 150^\circ, 390^\circ, 510^\circ \dots) \right ).\)
Если посчитать, синус перечисленных углов соответствует 1/2.
Если рассмотреть множество значений обратной тригонометрической функции, то можно получить ключевые ее значения. Данные значения подразумевают при упоминании арксинуса, арккосинуса и других аркфункций.
Предположим, что:
\( -1\leqslant \alpha \leqslant 1.\)
Тогда каждое из решений уравнения \(\sin x=\alpha\) допустимо записать, как:
\(x=(-1)^{n}\arcsin \alpha +\pi n,~n=0,\pm 1,\pm 2,\dots ~\)
Здесь -1 записано в n степени. Значения функций можно не считать, а посмотреть в таблице.
При нахождении ответов в процессе решения задач, в условии которых присутствуют такие функции, как: синус, косинус, тангенс, котангенс угла, обратные им функции — арксинус, арккосинус, арктангенс, арккотангенс — определяют угол. В том случае, когда речь в задании идет о тригонометрических функциях числа, то аркфункции также будут определяться в виде числа.
Арксинус числа а \(\in [−1, 1]\) является числом \(t\in [−\frac{\pi}{2}\), \(\frac{\pi}{2}]\) с синусом, равным а.
Арккосинус числа \(а \in [−1, 1]\) является числом \(t\in [0, \pi]\) с косинусом, равным а.
Арктангенс числа а \(\in (−\infty, \infty)\) является числом \(t\in(-\frac{\pi}{2}\), \(\frac{\pi}{2})\) с тангенсом, равным а.
Арккотангенс числа а \(\in (−\infty, \infty)\) является числом \(t\in (0, \pi)\) с котангенсом, равным а. В данном случае используют знак бесконечности, когда речь идет об определении а.
Представим, что имеется число, арксинус которого равен \(-\frac{1}{2}\). Тогда нужным числом является \(-\frac{\pi}{6}\) со знаком минус. В результате:
\(\arcsin (-\frac{1}{2}) = -\frac{\pi}{6}\)
В данном случае:
\(a = -\frac{1}{2}\)
\(t = -\frac{\pi}{6}\)
В действительности:
\(-\frac{1}{2}\in [-1, 1]\)
\(-\frac{\pi}{6}\in[−\frac{\pi}{2}, \frac{\pi}{2}]\)
\(\sin (-\frac{\pi}{6}) = -\frac{1}{2}\)
Важно различать задачи, где аркфункции являются числами, а где — углами. Данное условие можно понять по контексту. Если указана обратная тригонометрическая функция а без каких-либо уточнений, то ее допускается определять, как аркфункцию а в виде угла или числа.
В том случае, когда в записи обратной тригонометрической функции присутствуют градусы с минутами или радианы, к примеру, \(\arcsin a+10°\), подразумевается вычисление данной аркфункции в виде угла с определенной градусной мерой или в радианах.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так