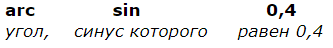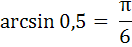Как найти арксинус: формула, свойства, функция

Понятие арксинуса

Обратные тригонометрические функции называют по соответствующим им тригонометрическим функциям. Формулировка наименования заключается в приписывании приставки «арк», что является производным от латинского слова «дуга» (arcus).

Такая методика объясняется тем, что в геометрии функцию, обратную тригонометрической, связывают с длиной, которую имеет дуга единичной окружности, равной какому-то отрезку, либо с углом, стягивающим данную дугу. В результате с помощью синуса можно, учитывая дугу окружности, определить хорду, которая ее стягивает.

Обратная функция под названием арксинус призвана решить противоположную задачу. Арксинус обозначают \(\arcsin x\) и определяют, как угол с синусом, равным х.

Для тригонометрических функций характерна периодичность. В связи с этим, обратные тригонометрические функции являются многозначными. Аркфункция обладает значением в виде множества из углов, для которых прямая тригонометрическая функция соответствует заданному числу.

Как правило, под обратными тригонометрическими функциями понимают ключевые значения каждой аркфункции, выделенные из ее множества значений.

Если \(-1\leqslant \alpha \leqslant 1\), то любое решение уравнения \(\sin x=\alpha\) записывают в такой форме: \( x=(-1)^{n}\arcsin \alpha +\pi n,~n=0,\pm 1,\pm 2,\dots \)~

Зачем нужен арксинус

С помощью аркфункций, в том числе — арккосинуса, арктангенса, арккотангенса, арксинуса — определяют углы треугольника. Подобное действие доступно при наличии информации о сторонах данной геометрической фигуры.

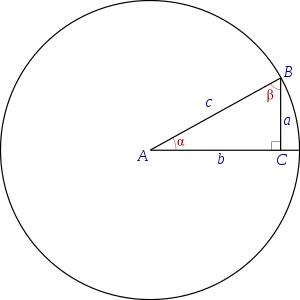
В том случае, когда имеется некий прямоугольный треугольник, обратные тригонометрические функции от отношений сторон позволяют определить угол. Например, длина катета составляет «а». Этот катет определяется, как противолежащий для угла \(\alpha\), то:

\(\alpha =\arcsin(a/c)=\arccos(b/c)=\operatorname {arctg} (a/b)=\operatorname {arccosec} (c/a)=\operatorname {arcsec}(c/b)=\operatorname {arcctg} (b/a)\)

Получение функции arcsin с пояснением на примерах

Предположим, что существует некая функция:

\(y=\sin x\)

Записанная функция обладает областью определения. В ее рамках она приобретает кусочно-монотонный вид. По этой причине обратное выражение y=\arcsin x нельзя причислить к функциям.

В результате целесообразно проанализировать отрезок, где наблюдается строгое возрастание функции, и все значения относятся к ряду из области значений:

\(\left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]\)

Функция \(y=\sin x \) на отрезке \(\left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]\) обладает следующей особенностью: какое-либо из значений этой функции возможно только при одном значении аргумента. По этой причине на данном интервале может существовать обратная функция с формулой \(y=\arcsin x.\)

График обратной функции является симметричным графику функции \(y=\sin x\) в рамках интервала \(\left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]\) по отношению к прямой y=x. Можно наблюдать симметричность в расположении графиков функций, которые являются взаимно обратными, по отношению к биссектрисе первого и третьего координатных углов на плоскости координат Oxy.

По определению обратной тригонометрической функции можно сделать вывод, что запись означает угол с синусом, равным 0,4. В данном выводе заключается смысл понятия арксинус.

Если знать определение, эта простая обратная тригонометрическая функция является обозначением угла с синусом, равным 0,5. Таким синусом обладает угол в 30°. Таким образом:

\(\arcsin 0,5 = 30°\)

Общий ответ можно высчитать не в градусах, а в радианах:

Свойства функции arcsin

Рассмотрим функцию \(y=\arcsin x\). Она является непрерывной в тригонометрии и ограничивается на протяжении всей своей области определения. Данная функция строго возрастает.

Область определения, в которой функцию можно вычислить:

\(D(\arcsin x)=[-1;1]\qquad\) (от минус единицы до плюс единицы)

Область значений:

\(E(\arcsin x)=\left[-{\frac {\pi }{2}};{\frac {\pi }{2}}\right]\qquad \)

Значения функций можно посчитать таким образом:

• \(\sin(\arcsin x)=x\qquad\), если \(-1\leqslant x\leqslant 1\)
• \(\arcsin(\sin y)=y\qquad\), если \(-{\frac {\pi }{2}}\leqslant y\leqslant {\frac {\pi }{2}}\)

Функция arcsin обладает следующими свойствами:

• \(\arcsin(-x)=-\arcsin x\qquad \)(нечетная функция);
• \(\arcsin x>0, когда 0<x\leqslant 1\);
• \(\arcsin x=0, когда x=0\);
• \(\arcsin x<0, если -1\leqslant x<0\);
• \(\arcsin x=\left\{{\begin{matrix}\arccos {\sqrt {1-x^{2}}},\qquad 0\leqslant x\leqslant 1\\-\arccos {\sqrt {1-x^{2}}},\qquad -1\leqslant x<0\end{matrix}}\right.\)
• \(\arcsin x=\operatorname {arctg}{\frac {x}{{\sqrt {1-x^{2}}}}}\);
• \(\arcsin x=\left\{{\begin{matrix}\operatorname {arcctg}\,{\frac {{\sqrt {1-x^{2}}}}{x}},\qquad 0<x\leqslant 1\\\operatorname {arcctg}\,{\frac {{\sqrt {1-x^{2}}}}{x}}-\pi ,\qquad -1\leqslant x<0\end{matrix}}\right.\)

График арксинуса

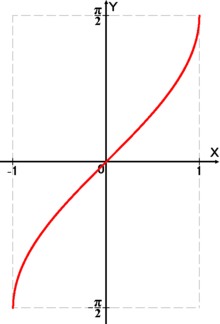
График функции \(y=\arcsin x\):