Биссектриса угла

Что такое биссектриса в геометрии

В треугольнике может быть три биссектрисы, так как данная геометрическая фигура содержит в себе три вершины.

Основные свойства биссектрисы треугольника

Приведем несколько теорем, касающихся свойств рассматриваемого отрезка, который расположен в треугольнике.

Теорема 1

Доказательство

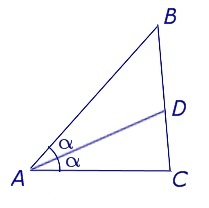
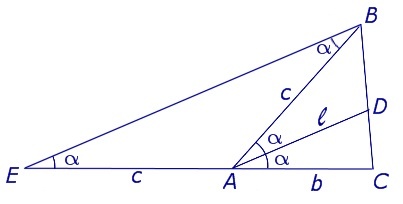
Продолжим сторону AC ΔABC, изображенного на рисунке 1, за точку A. Проведем через B прямую, которая параллельна AD. Обозначим точку пересечения построенных прямых буквой E.

Докажем, что отрезки AB и AE равны.

Для этого заметим, что ∠EBA равен ∠BAD, поскольку эти углы являются внутренними накрест лежащими при параллельных прямых EB и AD.

Заметим также, что ∠BEA=∠DAC, поскольку эти углы являются соответственными при параллельных прямых EB и AD.

Таким образом, ∠EBA=∠BEA, откуда вытекает, что ΔЕАВ является равнобедренным, и величина отрезков AB и AE равна.

Отсюда, воспользовавшись теоремой Фалеса, получаем:

\(\frac{ЕА}{АС}=\frac{BD}{DC}\Leftrightarrow\frac{AB}{AC}=\frac{BD}{DC}\)

Теорема доказана.

Следствие 1

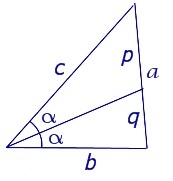
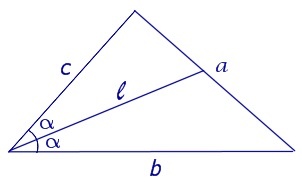
Рассмотрим рисунок, на котором изображен тот же треугольник, как и на первом изображении, но для длин отрезков использованы обозначения:

\(b=\left|AC\right|,\;a=\left|BC\right|,\;c=\left|AB\right|,\;p=\left|BD\right|,\;q=\left|DC\right|\)

Тогда: \(p=\frac{ac}{b+c},\;q=\frac{ab}{b+c}\)

Доказательство

\(\Leftrightarrow\left\{\begin{array}{l}p+q=a,\\\frac qp=\frac bc\end{array}\right.\)

\(\Leftrightarrow\left\{\begin{array}{l}p+q=a,\\q=\frac bcp\end{array}\right.\)

\(\Leftrightarrow\left\{\begin{array}{l}p+\frac bcp=a,\\q=\frac bcp\end{array}\right.\)

\(\Leftrightarrow\left\{\begin{array}{l}p=\frac{ac}{b+c},\\q=\frac bcp\end{array}\right.\)

\(\Leftrightarrow\left\{\begin{array}{l}p=\frac{ac}{b+c},\\q=\frac{ab}{b+c}\end{array}\right.\)

Следствие доказано.

Следствие 2

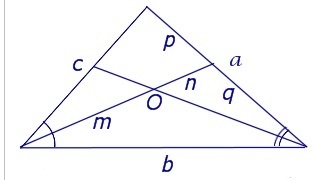
Рассмотрим рисунок, на котором изображены две биссектрисы, пересекающиеся в точке O:

Тогда справедлива формула:

\(\frac mn=\frac{b+c}a\)

Доказательство

Так как \(\frac mn=\frac bq,\;q=\frac{ab}{b+c},\)то:

\( \frac mn=\frac bq=\frac b{\left({\displaystyle\frac{ab}{b+c}}\right)}=\frac{b\left(b+c\right)}{ab}=\frac{b+c}a\)

Следствие доказано.

Теорема 2

Доказательство

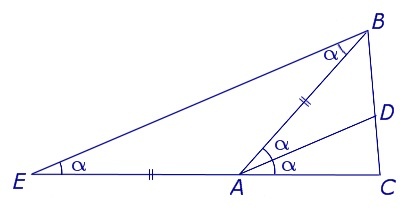
Из изображения следует формула: 

\(\left|ЕВ\right|=2с\;\cos\;\alpha\)

Если использовать это равенство, то из подобия треугольников ADC и EBC получим:

\(\frac{\left|AD\right|}{\left|EB\right|}=\frac b{b+c}\Leftrightarrow\frac l{2c\;\cos\;\alpha}=\frac b{b+c}\Leftrightarrow l=\frac{2bc}{b+c}\cos\;\alpha\)

Теорема доказана.

Теорема 3

Доказательство

Воспользуемся теоремой косинусов:

\(\cos\;2\alpha=\frac{b^2+c^2-a^2}{2bc}\)

Далее применим теорему косинуса двойного угла:

\(\cos^2\alpha=\frac12\left(1+\cos\;2\alpha\right)=\frac12\left(1+\frac{b^2+c^2-a^2}{2bc}\right)=\frac{b^2+2bc+c^2-a^2}{4bc}\)

Из этого следует, что

\(\cos\;\alpha=\frac12\sqrt{\frac{b^2+2bc+c^2-a^2}{bc}}\)

Откуда с помощью второй теоремы получаем:

\(l=\frac{2bc}{b+c}\cos\;\alpha=\frac{2bc}{b+c}\times\frac12\sqrt{\frac{b^2+2bc+c^2-a^2}{bc}}=\frac{\sqrt{bc\left(b^2+2bc+c^2-a^2\right)}}{b+c}\)

Что и требовалось доказать.

Применение биссектрисы на практике

Биссектриса применяется не только при нахождении ответа для математических задач. На самом деле без знания этого понятия и его сути невозможно обойтись во многих сферах. Например:

• при строительстве крыши;
• при защите радиовысотомеров от радиолокационных ракет;
• при конструировании кораблей;
• при исследовании следов орудий взлома и так далее.