Понятие четной и нечетной функции
Понятие четности и нечетности функции
Главное условие при исследовании функции на четность/нечетность — это симметричность области определения относительно 0. Если она не симметрична, то функция не является ни четной, ни нечетной, и дальнейшее исследование производить не нужно. Например, \(D(y)\in(-\infty;+\infty)\) симметрична относительно 0, а \(D(y):x\in(-5;9)\) — нет.
Четная функция
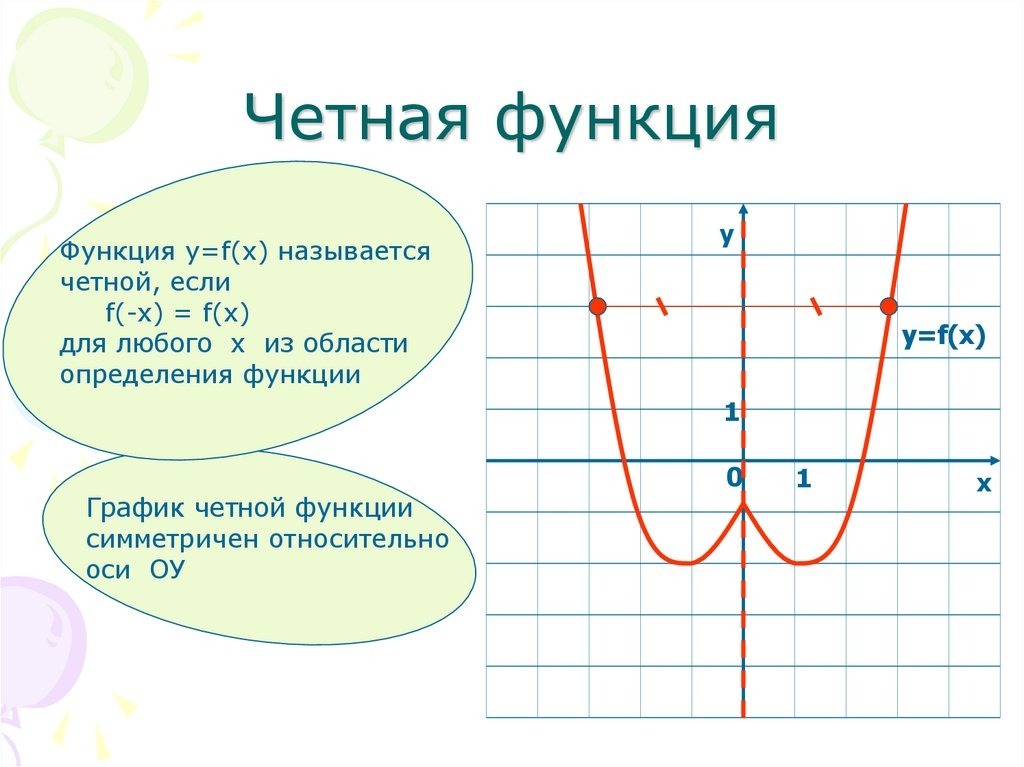
Функцию \(f(x)\) называют четной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=f(x).\)
Свойство:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
График четной функции симметричен относительно оси Ох.
Доказательство:
Возьмем произвольную точку \(M(x,\;f(x))\) из области определения \(f(x)\), тогда точка \(M_1(-x,\;f(x))\) так же будет принадлежать графику, что следует из определения. Значит график данной функции будет симметричен относительно оси ординат.
Нечетная функция
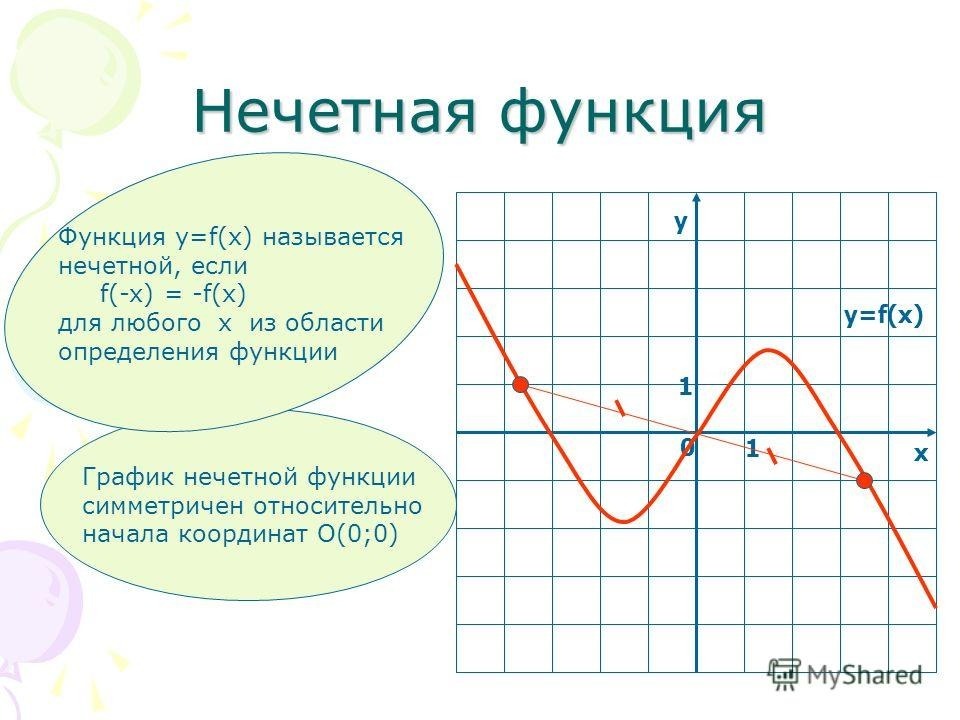
Функцию \(f(x)\) называют нечетной, если для любого значения х из области определения функции \(f(x)\) соблюдается равенство \(f(-x)=-f(x).\)
Свойство:
График нечетной функции симметричен относительно начала координат (точки (0;0)).
Доказательство:
Возьмем произвольную точку \(M(x,\;f(x))\) из области определения \(f(x)\), тогда точка \(M_1(-x,\;-f(x))\) также будет принадлежать графику, что следует из определения. Значит график данной функции будет симметричен относительно начала координат.
Произведение четной и нечетной функции
Произведение четной и нечетной функций есть нечетная функция.
Доказательство:
Пусть \(f(x)\) — четная функция, а \(g(x)\) — нечетная. Тогда \(f(x)=f(-x), а g(-x)=-g(x).\)
\(f(x)\cdot g(x)=(f\cdot g)(x)\)
\((f\cdot g)(-x)=f(-x)\cdot g(-x)=f(x)\cdot(-g(x))=-f(x)\cdot g(x)=-(f\cdot g)(x)\)
Значит, \((f\cdot g)(-x)=-(f\cdot g)(x)\), т.е. функция нечетная.
Теорема доказана.
Исследование функций в примерах
Доказать, что функция \(y=x^2\) четная.
1. Найдем область определения: \(D(y):x\in(-\infty;+\infty)\) — симметрична относительно 0.
2. \(f(x)=x^2\)
\(f(-x)=x^2\)
\(f(x)=f(-x)\), значит функция четная.
Исследовать на четность и нечетность функцию \(f(x)=8x^3-7x.\)
1. Найдем область определения: \(D(f):x\in(-\infty;+\infty)\) — симметрична относительно 0.
2. \(f(x)=8x^3-7x\)
\(f(-x)=-8x^3+7x\)
\(f(x)\neq f(-x)\), значит функция не является четной.
\(-f(x)=-8x^3+7x\)
\(-f(x)=f(-x)\), значит функция нечетна.
Исследовать на четность и нечетность функции \(f_1(x)=\frac{x^2}{x-1}\) и \(f_2(x)=\frac4{x^2-1}\)
Рассмотрим первую функцию:
1. Найдем область определения: x — любое число, кроме 1. Она не симметрична относительно 0, значит\( f_1(x)\) относится к функциям общего вида, то есть не является ни четной ни нечетной.
Рассмотрим вторую функцию:
1. Найдем область определения: х — любое число кроме -1 и 1. Она симметрична относительно 0.
2. \(f_1(x)=\frac4{x^2-1}\)
\(f_1(-x)=\frac4{x^2-1}\)
\(f_1(x)=f_1(-x)\), значит функция четная.
Заметили ошибку?
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Нашли ошибку?
Текст с ошибкой:
Расскажите, что не так